Bab 8 Bulatan III – user's Blog!

8.2.1 Sudut di antara Tangen dengan Perentas (Contoh Soalan)

Contoh 2:

Dalam rajah, PQR ialah tangen kepada bulatan QSTU di titik Q.

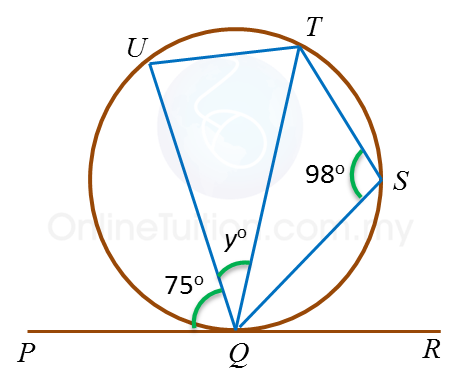
Cari nilai bagi y.

Penyelesaian:

∠QUT = 180^o– 98^o ← (sudut bertentangan dalam sisi empat kitaran QSTU)

= 82^o

∠QTU = 75^o ← (sudut dalam tembereng selang-seli)

Oleh itu y = 180^o – (82^o + 75^o) ← (Jumlah sudut dalaman ∆ QTU)

= 23^o

Contoh 3:

Dalam rajah, PQR ialah tangen kepada bulatan QSTU di titik Q.

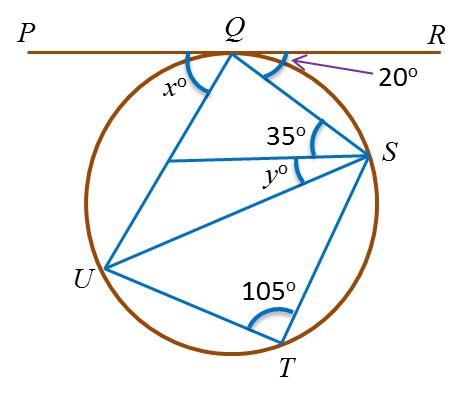Cari nilai bagi
(a) x
(b) y

Penyelesaian:

(a)

∠UTS + ∠UQS = 180^o ← (sudut bertentangan dalam sisi empat kitaran QSTU)

105^o + ∠UQS = 180^o

∠UQS = 75^o

x + 75^o + 20^o = 180^o ← (Jumlah sudut garis lurus PQR = 180^o)

x + 95^o = 180^o

x = 85^o

(b)

∠PQU = ∠QSU ← (sudut dalam tembereng selang-seli)

85^o = 35^o + y

y = 50^o

Contoh 4:

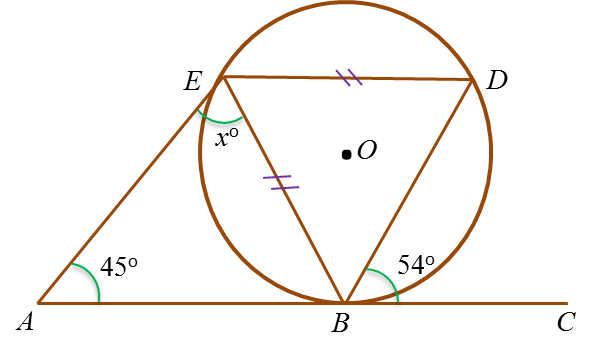
Dalam rajah, ABC ialah tangen kepada bulatan BDE dengan pusat O, di titik B.

Cari nilai bagi x.

Penyelesaian:

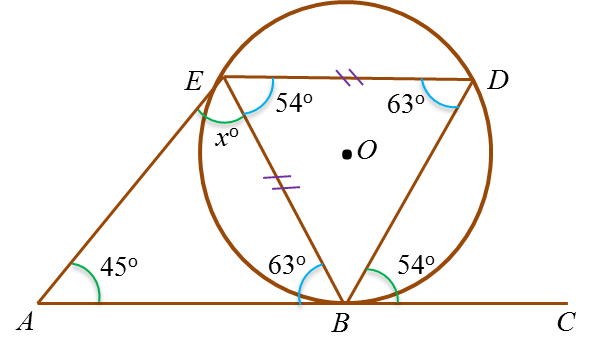
\begin{array}{l} ∠ B E D = ∠ C B D = 54^{\circ} \\ ∠ B D E \\ = \frac{180^{\circ} - 54^{\circ}}{2} = 63^{\circ} \leftarrow \begin{array}{l} Segi tiga kaki sama \\ ∠ E B D = ∠ E D B \end{array} \end{array}

∠ABE = ∠BDE = 63^o

Dalam ∆ABE,

x^o+ 45^o+ 63^o= 180^o

x^o+ 108^o= 180^o

x = 72