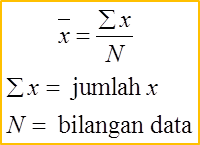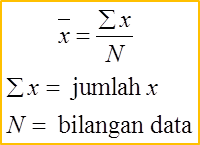Bab 7 Statistik

Posted on May 30, 2016 by user

7.1a Min

$Min = \frac{Hasil tambah nilai data}{Bilangan data}$

(A) Data Tak Terkumpul

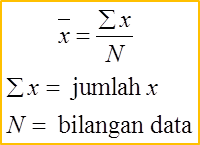
Contoh 1:

(a) Cari min bagi set data 2, 4, 7, 10, 13, 16 dan 18.

(b) Apabila suatu nilai x ditambah ke dalam set data di (a), nilai baru min menjadi 9.5. Tentukan nilai x.

Penyelesaian:

(a)

$\begin{array}{l} \bar{x} = \frac{2 + 4 + 7 + 10 + 13 + 16 + 18}{7} \\ \bar{x} = \frac{70}{7} = 10 \end{array}$

(b)

$\begin{array}{l} Min baru = 9.5 \\ \frac{70 + x}{8} = 9.5 \\ 70 + x = 76 \\ x = 6 \end{array}$

(B) Data Terkumpul (tanpa Selang Kelas)

Contoh 2:

Jadual kekerapan yang berikut menunjukkan markah ujian biologi bagi 40 orang pelajar.

Kira min markah.

Penyelesaian:

$\begin{array}{l} Min markah, \bar{x} \\ \bar{x} = \frac{(50) (6) + (55) (8) + (60) (15) + (65) (10) + (70) (1)}{6 + 8 + 15 + 10 + 1} \\ \bar{x} = \frac{2360}{40} = 59 \end{array}$

(C) Data Terkumpul (dengan Selang Kelas)

Contoh 3:

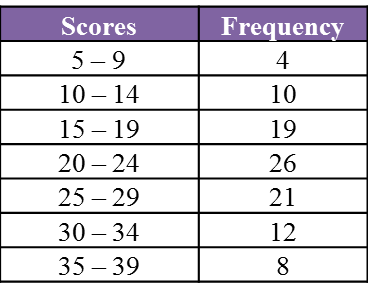
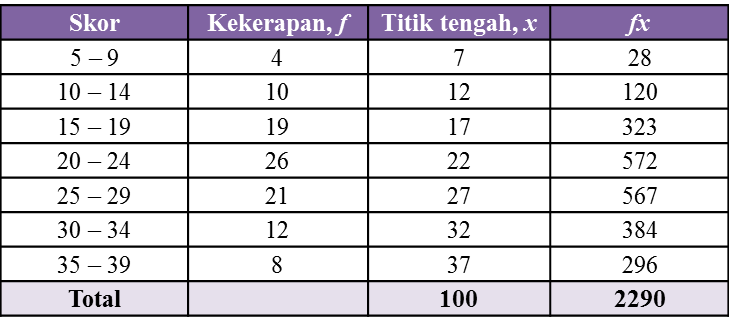
Jadual yang berikut menunjukkan taburan kekerapan skor yang diperoleh 100 pelajar dalam
suatu pertandingan.

Kira min skor.

Penyelesaian:

$\begin{array}{l} Nilai tengah = \frac{5 + 9}{2} = 7 \\ Min skor, \bar{x} = \frac{\sum f x}{\sum f} = \frac{2290}{100} = 22.9 \end{array}$