9.2.1 Loci in Two Dimensions, PT3 Focus Practice
Question 1:
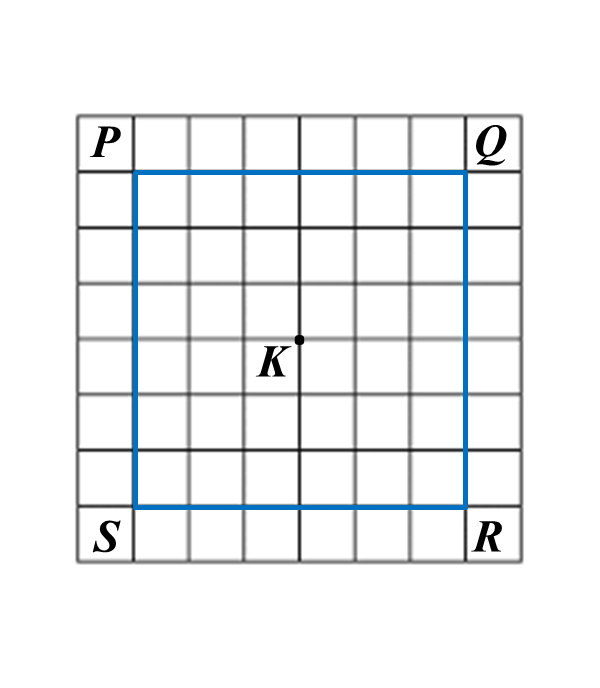
Diagram below in the answer space shows a square PQRS with sides of 6 units drawn on a grid of equal squares with sides of 1 unit. W, X and Y are three moving points inside the square.
(a) W is the point which moves such that it is always equidistant from point P and point R.
By using the letters in diagram, state the locus of W.
(b) On the diagram, draw,
(i) the locus of the point X which moves such that it is always equidistant from the straight lines PQ and PS,
(ii) the locus of the point Y which moves such that its distance is constantly 2 units from point K.
(c) Hence, mark with the symbol ⊗ the intersection of the locus of X and the locus of Y.
Answer:
(b)(i),(ii)

Solution:
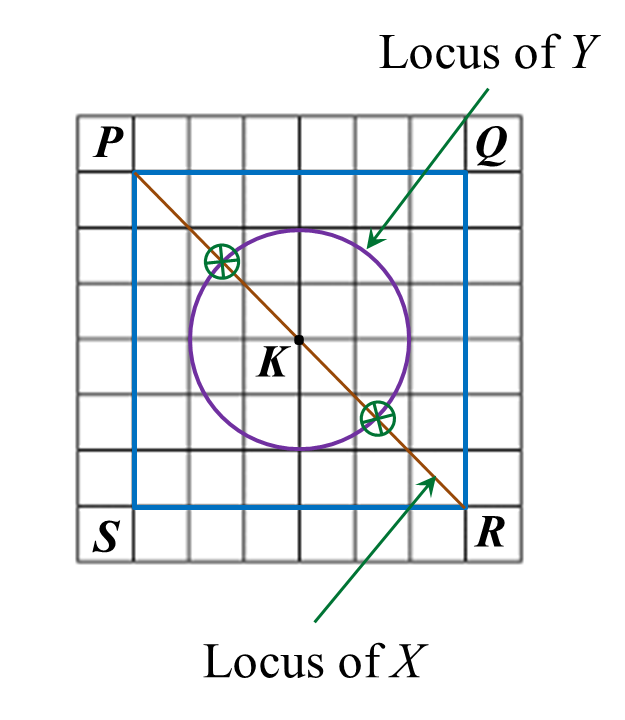
(a) QS
(b)(i),(ii)
(c)
Question 2:
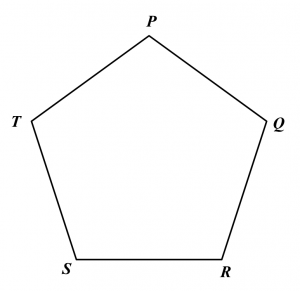
Diagram in the answer space below, shows a regular pentagon PQRST. W, X and Y are moving points which move in the pentagon.
On the diagram,
(a) draw the locus of the point W which moves such that it is always equidistant from point R and S.
(b) draw the locus of the point X which moves such that XR = RS.
(c) draw the locus of point Y which moves such that its distance is constantly 3 cm from the line SR.
(d) hence, mark with the symbol ⊗ the intersection of the locus of W and the locus of X.
Answer:
(a), (b), (c) and (d)
Solution:
(a), (b), (c) and (d)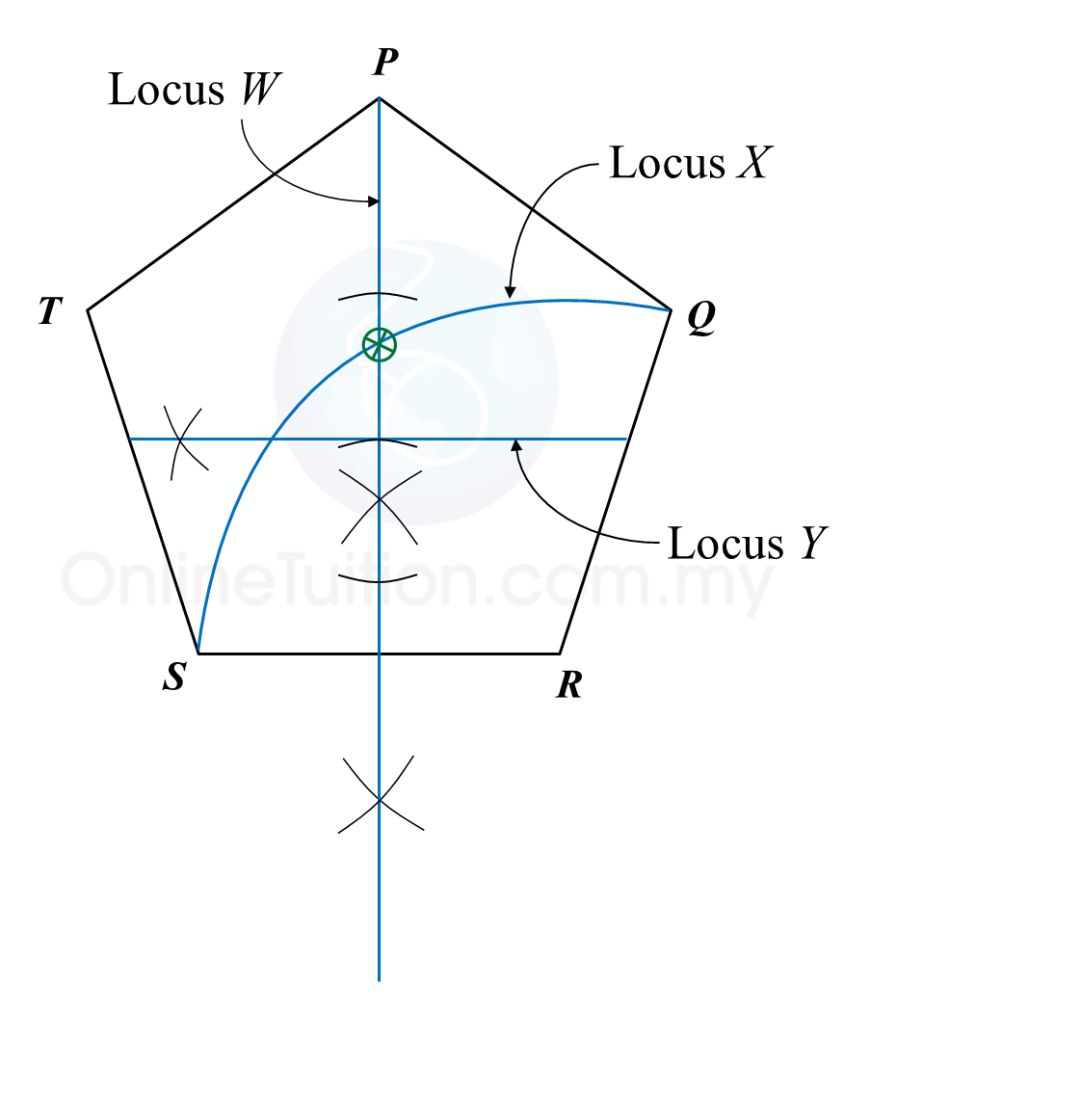
Question 3:
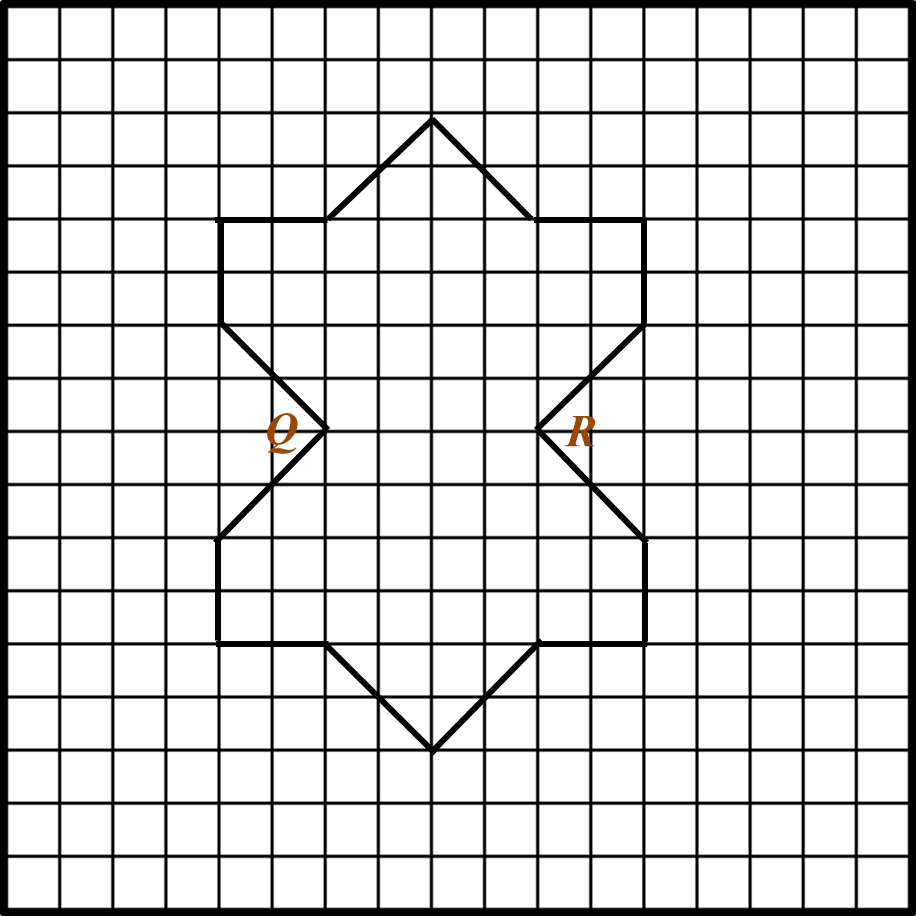
Diagram in the answer space below shows a polygon. X and Y are two moving points in the polygon.
(a) On the diagram, draw
(i) the locus of the point X such that XQ = XR.
(ii) the locus of the point Y such that YQ = QR.
(b) Hence, mark with the symbol the intersection of the locus of X and the locus of Y.
Answer:

Diagram in the answer space below shows a polygon. X and Y are two moving points in the polygon.
(a) On the diagram, draw
(i) the locus of the point X such that XQ = XR.
(ii) the locus of the point Y such that YQ = QR.
(b) Hence, mark with the symbol the intersection of the locus of X and the locus of Y.
Answer:
(a)(i), (ii) and (b)

Solution:
(a)(i), (ii) and (b)