10.1 Circles I – user's Blog!

10.1 Circles I

10.1.1 Parts of a Circle

1. A circle is set of points in a plane equidistant from a fixed point.

2. Parts of a circle:

(a) The centre, O, of a circle is a fixed point which is equidistant from all points on the circle.

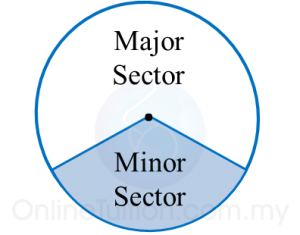
(b) A sector is the region enclosed by two radii and an arc.

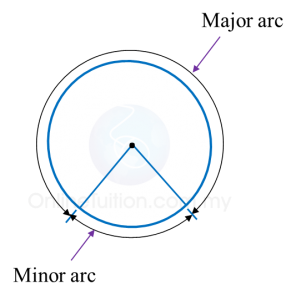
(c) An arc is a part of the circumference of a circle.

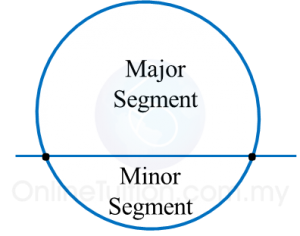
(d) A segment is an area enclosed by an arc and a chord.

10.1.2 Circumference of a Circle

$\begin{array}{l} circumference = π d, where d = d i a m e t e r \\ = 2 π r, where r = r a d i u s \\ π (p i) = \frac{22}{7} or 3.142 \end{array}$

Example:

Calculate the circumference of a circle with a diameter of 14 cm.

$(π = \frac{22}{7})$

Solution:

$\begin{array}{l} Circumference = π \times Diameter \\ = \frac{22}{7} \times 14 \\ = 44 cm \end{array}$

10.1.3 Arc of a Circle

The length of an arc of a circle is proportional to the angle at the centre.

$\begin{array}{l} \frac{Length of arc}{Circumference} = \frac{Angle at centre}{360^{o}} \end{array}$

Example:

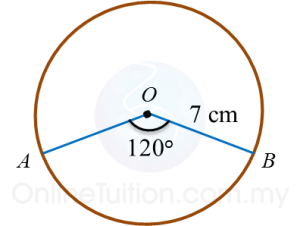
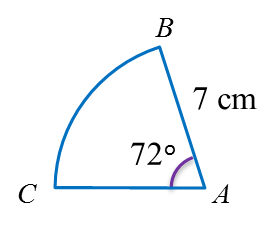
Calculate the length of the minor arc AB of the circle above.

$(π = \frac{22}{7})$

Solution:

$\begin{array}{l} \frac{Length of arc}{Circumference} = \frac{Angle at centre}{360^{o}} \\ Length of arc A B = \frac{120^{o}}{360^{o}} \times 2 \times \frac{22}{7} \times 7 \\ = 14 \frac{2}{3} cm \end{array}$

10.1.4 Area of a Circle

$\begin{array}{l} Area of a circle = π \times {(radius)}^{2} \\ = π r^{2} \end{array}$

Example:

Calculate the area of each of the following circles that has

(a) a radius of 7 cm,

(b) a diameter of 10 cm.

$(π = \frac{22}{7})$

Solution:

(a)

$\begin{array}{l} Area of a circle = π r^{2} \\ = \frac{22}{7} \times 7 \times 7 \\ = 154 {cm}^{2} \end{array}$

(b)

$\begin{array}{l} Diameter of circle = 10 cm \\ Radius of circle = 5 cm \\ Area of circle = π r^{2} \\ = \frac{22}{7} \times 5 \times 5 \\ = 78.57 {cm}^{2} \end{array}$

10.1.5 Area of a Sector

The area of a sector of a circle is proportional to the angle at the centre.

$\begin{array}{l} \frac{Area of sector}{Area of circle} = \frac{Angle at centre}{360^{o}} \end{array}$

Example:

$\begin{array}{l} Area of sector A B C \\ = \frac{72^{o}}{360^{o}} \times \frac{22}{7} \times 7 \times 7 \\ = 30 \frac{4}{5} {cm}^{2} \end{array}$