3.2.1 Circles II, PT3 Practice

3.2.1 Circles II, PT3 Practice

Question 1:

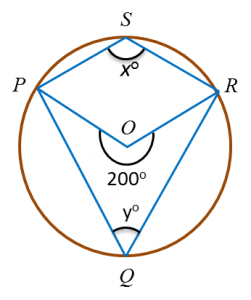
(a) In Diagram below, KLM, LPN and MPO are straight lines.

Find the value of x and of y.

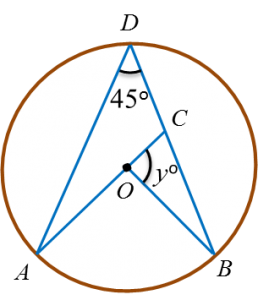
(b) In the diagram below, O is the centre of the circle. Find the value of

(i) x (ii) y

Solution:

(a)

$\begin{array}{l} ∠ L O M = ∠ L N M = y^{o} = 44^{o} \\ ∴ y = 44 \\ ∠ N M O = ∠ N L O = 41^{o} \\ x^{o} = 180^{o} - 80^{o} - 41^{o} \\ = 59^{o} \end{array}$

(b)(i)

2x = 200^o

x = 100^o

(b)(ii)

x + y = 180^o

100^o + y = 180^o

y = 80^o

Question 2:

(a) In Diagram below, AOC and BCD are straight lines with centre O.

Find the value of y.

(b) In diagram below, ABCD is a circle with centre O and ADE is a straight line.

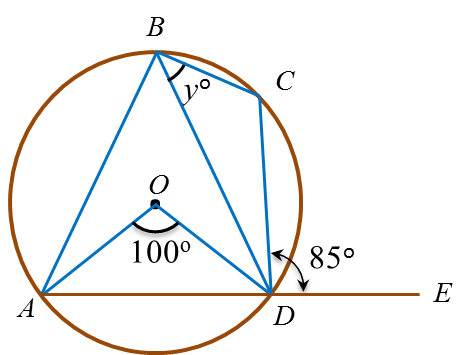
Find the value of y.

Solution:

(a)

$\begin{array}{l} ∠ A O B = 45^{o} \times 2 = 90^{o} \\ y^{o} = 180^{o} - 90^{o} = 90^{o} \end{array}$

(b)

$\begin{array}{l} ∠ A B D = \frac{1}{2} \times 100^{o} = 50^{o} \\ ∠ C D E = ∠ A B C = 85^{o} \\ y^{o} + 50^{o} = 85^{o} \\ y^{o} = 35^{o} \\ y = 35 \end{array}$

Question 3:

(a) In diagram below, ABCD is a circle. AEC and BED are straight lines.

Find the value of y.

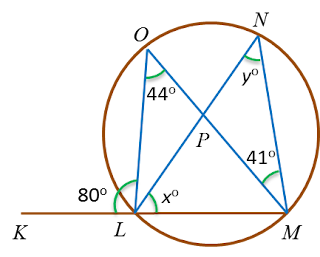
(b) Diagram below shows a circle KLMN with centre O.

Find the value of x.

Solution:

(a)

$\begin{array}{l} ∠ A B E = ∠ A C D = 45^{o} \\ y^{o} = 180^{o} - 45^{o} - 55^{o} \\ y^{o} = 80^{o} \\ y = 80 \end{array}$

(b)

$\begin{array}{l} ∠ O M L = ∠ O L M = 42^{o} \\ (x^{o} + 42^{o}) + ∠ K N M = 180^{o} \\ x^{o} + 42^{o} + 110^{o} = 180^{o} \\ x^{o} + 152^{o} = 180^{o} \\ x^{o} = 180^{o} - 152^{o} \\ x^{o} = 28^{o} \\ x = 28 \end{array}$

Question 4:

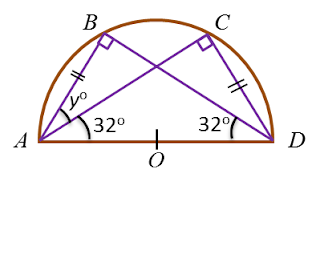
Diagram below shows a semicircle ABCD with centre O.

It is given that AB = CD.

Find the value of y.

Solution:

y^o+ 32^o + 32^o + 90^o = 180^o

y^o= 180^o – 154^o

y^o= 26^o

y = 26

Question 5:
In diagram below, ABC and DEF are straight lines.

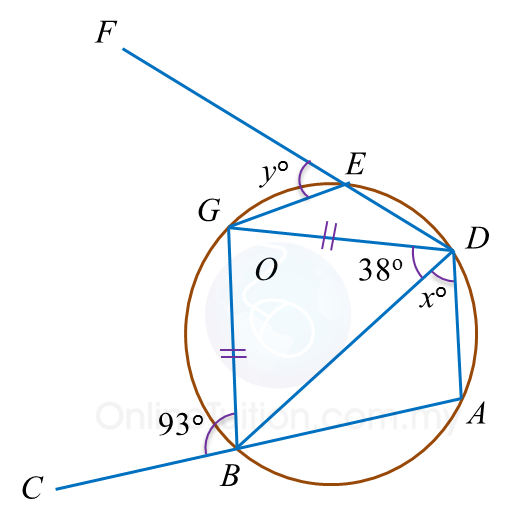
Find the value of x and of y.

Solution:

$\begin{array}{l} x + 38 = 93 \\ x = 93 - 38 \\ x = 55 \\ ∠ D B G = 38^{o} (G B = G D) \\ y^{o} = ∠ D B G \\ ∴ y = 38 \end{array}$