Question 4:
It is given the functions g(x) = 3x and h(x) = m – nx, where m and n are constants.
Express m in terms of n such that hg(1) = 4.
Solution:
It is given the functions g(x) = 3x and h(x) = m – nx, where m and n are constants.
Express m in terms of n such that hg(1) = 4.
Solution:
Question 5:
Diagram below shows the relation between set M and set N in the graph form.
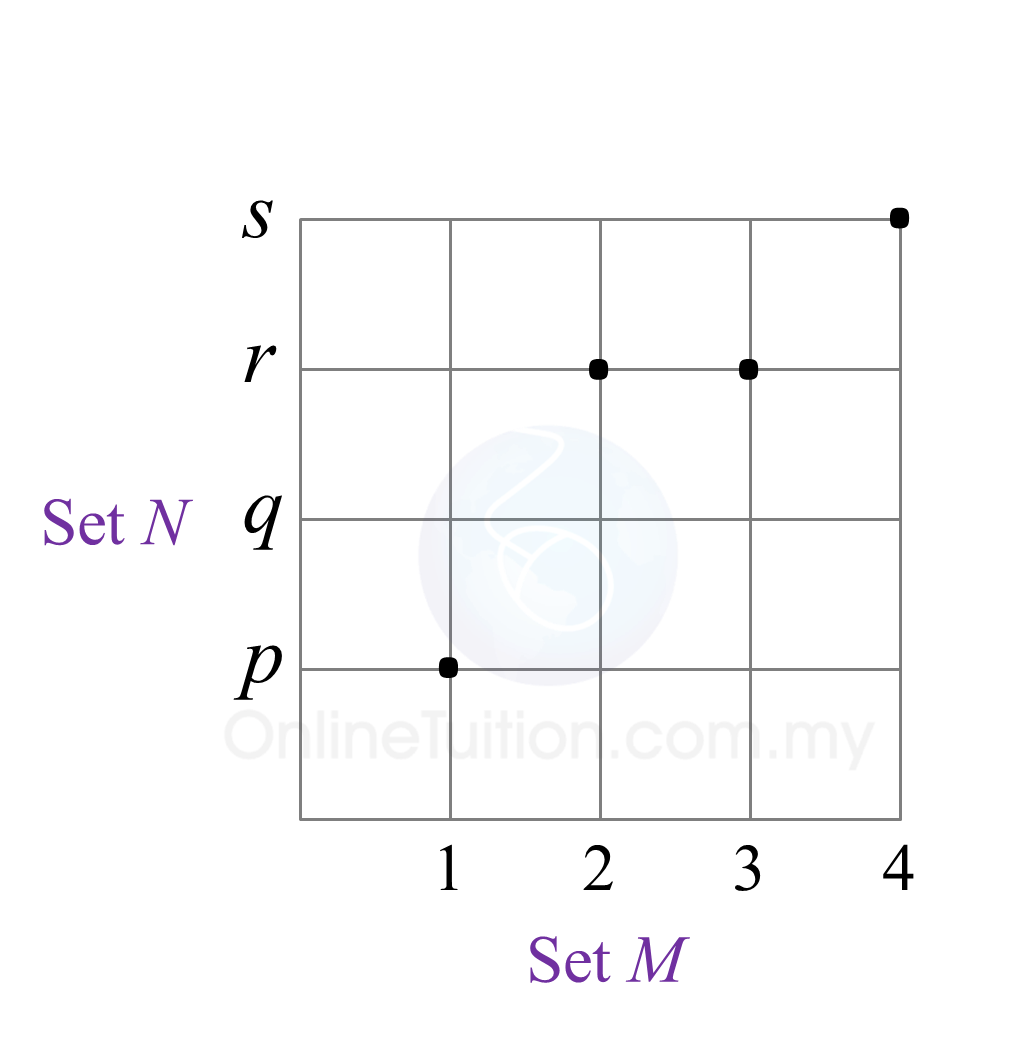 State
State
(a) the range of the relation,
(b) the type of the relation between set M and set N.
Solution:
(a) Range of the relation = {p, r, s}.
(b) Type of the relation between set M and set N is many to one relation.
Diagram below shows the relation between set M and set N in the graph form.
 State
State(a) the range of the relation,
(b) the type of the relation between set M and set N.
Solution:
(a) Range of the relation = {p, r, s}.
(b) Type of the relation between set M and set N is many to one relation.
Question 6:
Diagram below shows the relation between set P and set Q.

State
(a) the object of 3,
(b) the range of the relation.
Solution:
(a) The object of 3 is 7.
(b) The range of the relation is {–3, –1, 1, 3}.
Diagram below shows the relation between set P and set Q.

State
(a) the object of 3,
(b) the range of the relation.
Solution:
(a) The object of 3 is 7.
(b) The range of the relation is {–3, –1, 1, 3}.