9.2 Latitudes

Posted on April 24, 2020 by user

9.2 Latitudes

1. The great circle which is perpendicular to the earth’s axis is called equator.

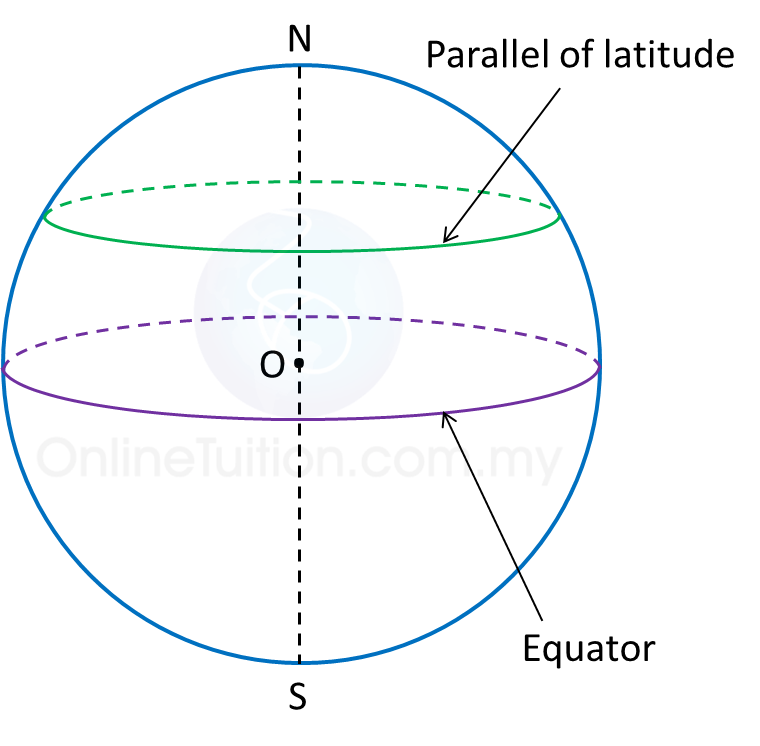
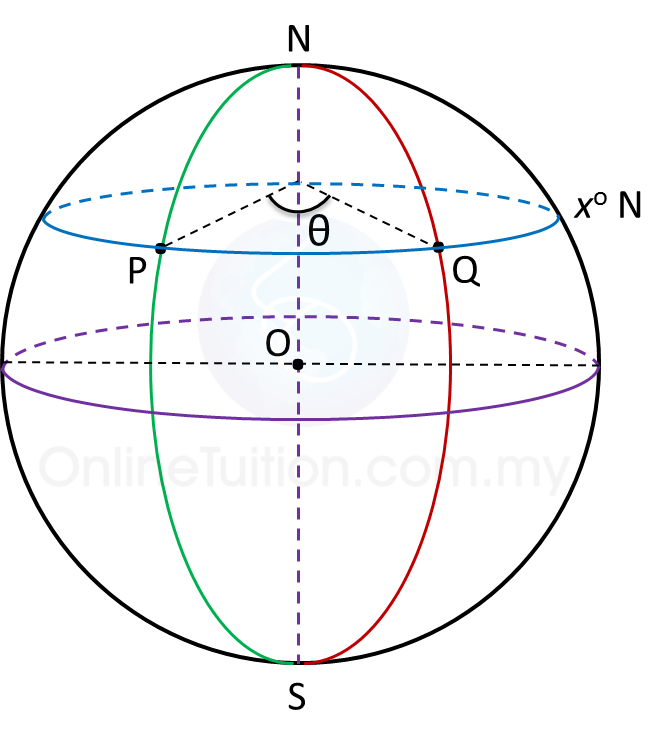
2. A latitude is the angle at the centre of the Earth which is subtended by the arc of a meridian starting from the Equator to the parallel of latitude.

3. A circle which is perpendicular to the Earth’s axis and parallel to the equator is called a parallel of latitude.

4. The latitude of the Equator is 0^o.

5. All points on a parallel of latitude have the same latitude.

Example:

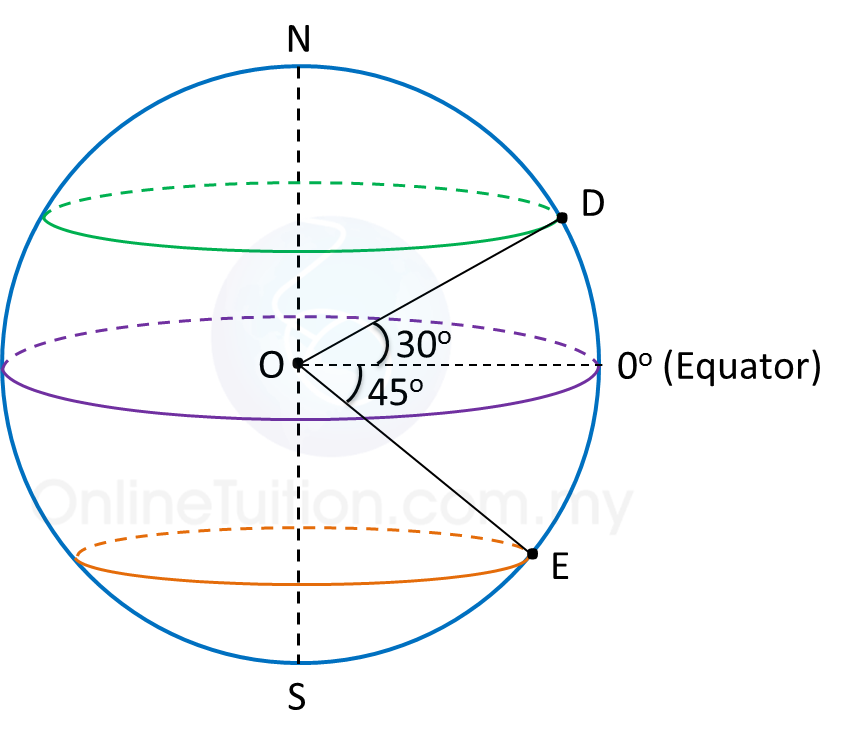
Latitude of D is 30^o N.

Latitude of E is 45^o S.

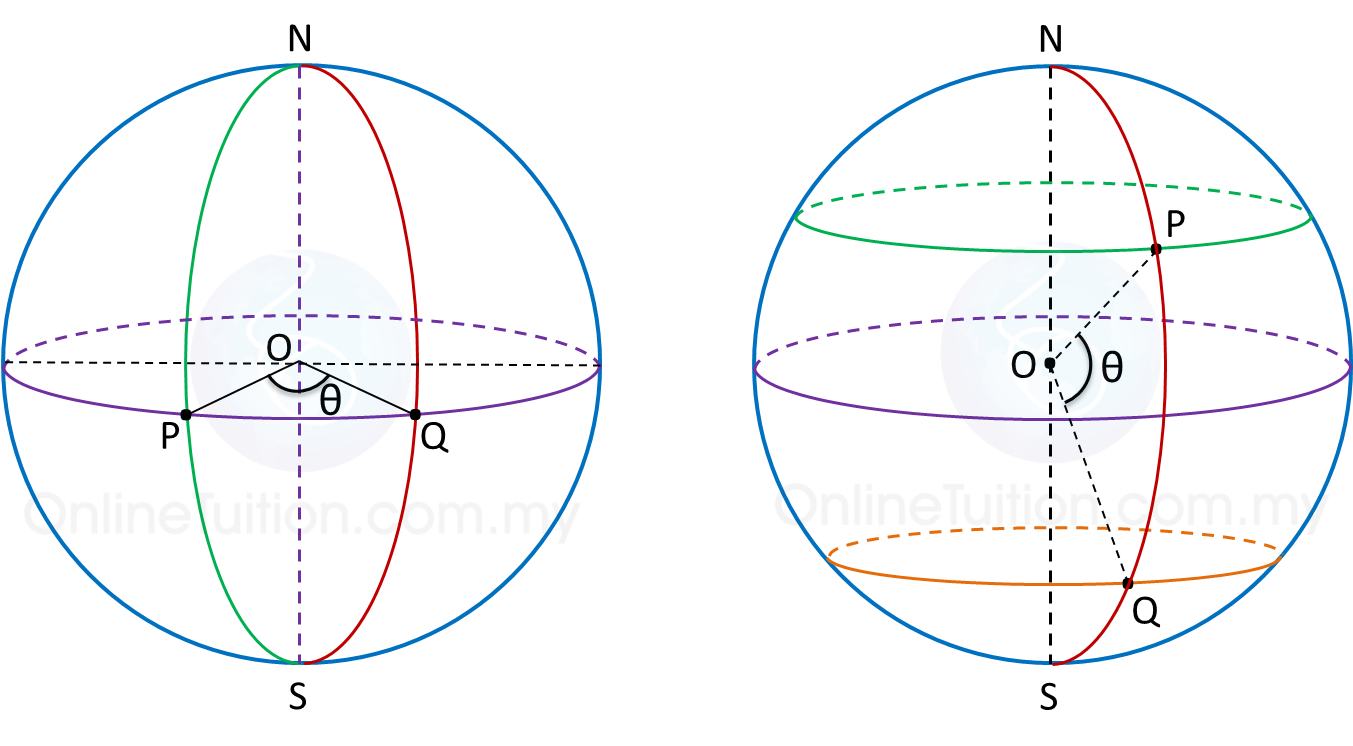
Difference between Two Latitudes

1. If both parallels of latitude are on the north (or south) of the equator, subtract the angles of latitudes.

2. If both parallels of latitude are on the opposite sides of the equator, add the angles of the latitudes.

9.4 Distance on the Surface of the Earth

Posted on April 24, 2020 by user

9.4 Distance on the Surface of the Earth

9.4.1 Distance between Two Points Along a Great Circle

1. A nautical mile is the length of an arc of a great circle that subtends an angle of one minute at the centre of the Earth.

2. The distance between two points on the surface of the earth is the arc of a circle that joins the two points.

3. To find the distance between two points along a meridian or the equator:

Distance of P and Q

= ( θ x 60 ) nautical miles

9.4.2 Distance between Two Points along a Parallel of Latitude

Posted on April 24, 2020 by user

9.4.2 Distance between Two Points along a Parallel of Latitude

1. To find the distance along a parallel of latitude:

Distance between points P and Q

= ( different in longitude in minutes ) × cos latitude

= ( θ × 60 × cos x^o ) nautical miles

Example:

In the diagram above, calculate

(a) The distance of PQ, measured along the parallel of latitude 34^o N,

(b) The distance of DM, measured along the parallel of latitude 54^o S.

Solution:

(a)

Difference in longitude between P and Q

= 40^o+ 58^o= 98^o

Hence, the distance of PQ, measured along the parallel of latitude 34^o N

= 98 × 60 × cos 34^o← [θ × 60 × cos (latitude)]

= 4874.74 n.m.

(b)

Difference in longitude between D and M

= 82^o– 40^o= 42^o

Hence, the distance of DM, measured along the parallel of latitude 54^o S

= 42 × 60 × cos 54^o← [θ × 60 × cos (latitude)]

= 1481.22 n.m.

7.2 Probability of the Complement of an Event

Posted on April 24, 2020 by user

7.2 Probability of the Complement of an Event

1. The complement of an event A is the set of all the outcomes in the sample space that are not included in the outcomes of event A.

2. The probability of the complement of event A is:

P (A') = 1 - P (A)

Example:

A number is chosen at random from a set of whole number from 1 to 40. Calculate the probability that the chosen number is not a perfect square.

Solution:

Let

A = Event of choosing a perfect square.

A’ = Event that the number is not a perfect square.

A = {1, 4, 9, 16, 25, 36}

n(A) = 6

\begin{array}{l} P (A) = \frac{n (A)}{n (S)} \\ = \frac{6}{40} = \frac{3}{20} \\ ∴ P (A') = 1 - P (A) \\ = 1 - \frac{3}{20} = \frac{17}{20} \\ Hence, the probability that the number chosen \\ is not a perfect square is \frac{17}{20} . \end{array}

7.4 SPM Practice (Short Questions)

Posted on April 24, 2020 by user

Question 1:
A bag contains 36 marbles which are black and white. It is given that the probability for a black marble being picked at random from the bag is

\frac{5}{9}

.
Calculate the number of white marbles to be taken out from the bag so that the probability of picking a black marble is

\frac{5}{8}

Solution:

\begin{array}{l} Number of black marbles in the bag \\ = \frac{5}{9} \times 36 = 20 \\ Let y is the total number of marbles left in the bag . \\ y \times \frac{5}{8} = 20 \\ y = 20 \times \frac{8}{5} = 32 \\ Number of white marbles to be taken out from the bag \\ = 36 - 32 \\ = 4 \end{array}

Question 2:

Table below shows the number of different coloured balls in three bags.

	Green	Brown	Purple
Bag A	3	1	6
Bag B	5	3	4
Bag C	4	6	2

If a bag is picked at random and then a ball is drawn randomly from that bag, what is the probability that a purple ball is drawn?

Solution:
Probability of picking a bag =

\frac{1}{3}

Probability of picking purple ball from bag A =

\frac{6}{10} = \frac{3}{5}

Probability of picking purple ball from bag B =

\frac{4}{12} = \frac{1}{3}

Probability of picking purple ball from bag C =

\frac{2}{12} = \frac{1}{6}

\begin{array}{l} P (purple ball) = (\frac{1}{3} \times \frac{3}{5}) + (\frac{1}{3} \times \frac{1}{3}) + (\frac{1}{3} \times \frac{1}{6}) \\ = \frac{1}{5} + \frac{1}{9} + \frac{1}{18} \\ = \frac{11}{30} \end{array}

Question 3:
A box contains 48 marbles. There are red marbles and green marbles. A marble is chosen at random from the box. The probability that a red marble is chosen is

\frac{1}{6} .

How many red marbles need to be added to the box so that the probability that a red marble is chosen is

\frac{1}{2} .

Solution:

\begin{array}{l} Number of red marbles in the box \\ = \frac{1}{6} \times 48 \\ = 8 \\ Let the number of red marbles needed to be added be y . \\ P (red marble) = \frac{1}{2} \\ \frac{8 + y}{48 + y} = \frac{1}{2} \\ 16 + 2 y = 48 + y \\ 2 y - y = 48 - 16 \\ y = 32 \\ ∴ Number of red marbles need to be added = 32 \end{array}

7.3 Probability of a Combined Event

Posted on April 24, 2020 by user

7.3 Probability of a Combined Event

7.3b Finding the Probability of Combined Events (a) A or B (b) A and B

1. The probability of a combined event ‘A or B’ is given by the formula below.

\begin{array}{l} P (A or B) = P (A \cup B) \\ = \frac{n (A \cup B)}{n (S)} \end{array}

2. The probability of a combined event ‘A and B’ is given by the formula below.

\begin{array}{l} P (A and B) = P (A \cap B) \\ = \frac{n (A \cap B)}{n (S)} \end{array}

Example:

The probabilities that two Form 5 students, Fiona and Wendy will pass the English oral test are

\frac{1}{3} and \frac{2}{5}

respectively. Calculate the probability that

(a) both Fiona and Wendy past the English oral test,
(b) both Fiona and Wendy fail the English oral test,

(c) either one of them passes the English oral test,
(d) at least one of them passes the English oral test.

Solution:

Let

F = Event that Fiona passes the English oral test

W = Event that Wendy passes the English oral test

Therefore,

F’ = Event that Fiona fails the English oral test

W’ = Event that Wendy fails the English oral test

\begin{array}{l} P (F) = \frac{1}{3}, P (F') = \frac{2}{3} \\ P (W) = \frac{2}{5}, P (W') = \frac{3}{5} \end{array}

(a)

P (both Fiona and Wendy past the English oral test)

= P (F ∩ W)

= P (F) x P (W)

\begin{array}{l} = \frac{1}{3} \times \frac{2}{5} \\ = \frac{2}{15} \end{array}

(b)

P (both Fiona and Wendy fail the English oral test)

= P (F’ ∩ W’)
= P (F’) x P (W’)

\begin{array}{l} = \frac{2}{3} \times \frac{3}{5} \\ = \frac{2}{5} \end{array}

(c)

P (either one of them passes the English oral test)

= P (F ∩ W’) + P (F’ ∩ W)
= (P (F) x P (W’)) + (P (F’) x P (W))

\begin{array}{l} = (\frac{1}{3} \times \frac{3}{5}) + (\frac{2}{3} \times \frac{2}{5}) \\ = \frac{7}{15} \end{array}

(d)

P (at least one of them passes the English oral test)

= 1 – P (Both of them fail) ← (concept of complement event)

= 1 – P (F’) x P (W’)

\begin{array}{l} = 1 - \frac{2}{5} \\ = \frac{3}{5} \end{array}

7.3 Probability of a Combined Event

Posted on April 24, 2020 by user

7.3 Probability of a Combined Event

7.3a Finding the Probability of a Combined Event by Listing the Outcomes

1. A combined event is an event resulting from the union or intersection of two or more events.

2. The union of combined event ‘A or B’ = A υ B

3. The intersection of combined event ‘A and B’ = A ∩ B

Example:

Diagram below shows five cards labelled with letters.

All these cards are put into a box. A two-letter code is to be formed by using any two of these cards. Two cards are picked at random, one after another, without replacement.

(a) List all sample space

(b) List all the outcomes of the events and find the probability that

(i) The code begins with the letter P.

(ii) The code consists of two vowel or two consonants.

Solution:

(a)

Sample space, S

= {(G, R), (G, A), (G, P), (G, E), (R, G), (R, A), (R, P), (R, E), (A, G), (A, R),

(A, P), (A, E), (P, G), (P, R), (P, A), (P, E), (E, G), (E, R), (E, A), (E, P)}

(b)

n(S) = 20

Let

A = Event of choosing a code begins with the letter P

B = Event of choosing the code consists of two vowel or two consonants.

(i)

A = {(P, G), (P, R), (P, A), (P, E)}

n(A) = 4

P (A) = \frac{4}{20} = \frac{1}{5}

(ii)

B = {(G, R), (G, P), (R, G), (R, P), (A, E), (P, G), (P, R), (E, A)}

n(B) = 8

P (B) = \frac{8}{20} = \frac{2}{5}

7.5 SPM Practice (Long Questions)

Posted on April 24, 2020 by user

Question 1:

All the cards written with the letters from the word ‘INTERNATIONAL’ are put into a box.

Two cards are drawn at random from the box, one after another, without replacement. Calculate the probability that

(a) the first card drawn has a letter N and the second card drawn has a letter I.

(b) the two cards drawn have the same letter.

Solution:
(a)
There are three cards with the letter ‘N’ and two card with letter ‘I’.
P (the first card drawn has a letter N and the second card drawn has a letter I)

\begin{array}{l} = \frac{3}{13} \times \frac{2}{(13 - 1)} \\ = \frac{3}{13} \times \frac{2}{12} = \frac{1}{26} \end{array}

(b)
P (the two cards drawn have the same letter)
= P (II or NN or TT or AA)
= P (II) + P (NN) + P (TT) + P (AA)

\begin{array}{l} = (\frac{2}{13} \times \frac{1}{12}) + (\frac{3}{13} \times \frac{2}{12}) + (\frac{2}{13} \times \frac{1}{12}) + (\frac{2}{13} \times \frac{1}{12}) \\ ↑ \\ \begin{array}{l} There are 3 letter ' N' \\ out of 13 letters \end{array} \\ = \frac{2}{156} + \frac{6}{156} + \frac{2}{156} + \frac{2}{156} \\ = \frac{12}{156} \\ = \frac{1}{13} \end{array}

Question 2:
During National Day celebration, a group of 8 boys and 5 girls from a school are taking part in a singing competition. Each day, two pupils are chosen at random to perform special skill.

(a) Calculate the probability that both pupils chosen to perform special skill are boys.

(b) Two boys were chosen to perform special skill on the first day. They are exempted from performing special skill on the second day.
Calculate the probability that both pupils chosen to perform special skill on the second day are of the same gender.

Solution:
(a)

\begin{array}{l} P (both pupils are boys) \\ = P (B B) \\ = \frac{8}{13} \times \frac{7}{12} \\ = \frac{7}{24} \end{array}

(b)

\begin{array}{l} P (both pupils are of the same gender) \\ = P (B B) + P (G G) \\ = (\frac{6}{11} \times \frac{5}{10}) + (\frac{5}{11} \times \frac{4}{10}) \leftarrow \begin{array}{l} 11 pupils left in the group to \\ perform special skill on the second \\ day after two boys were exempted . \end{array} \\ = \frac{3}{11} + \frac{2}{11} \\ = \frac{5}{11} \end{array}

7.1 Probability of an Event

Posted on April 24, 2020 by user

7.1 Probability of an Event

The probability of an event A, P(A) is given by

\begin{array}{l} P (A) = \frac{Number of times event A occurs}{Number of trials} \\ P (A) = \frac{n (A)}{n (S)} \\ where 0 \leq P (A) \leq 1 \end{array}

If P(A) = 0, then the event A will certainly not occur.

If P(A) = 1, then the event A is sure to occur.

Example 1:

A box contains 9 red pens and 13 blue pens. Tom puts another 4 red pens and 2 blue pens into the box. A pen is picked at random from the box. What is the probability that a red pen is picked?

Solution:

n(S) = 9 + 13 + 4 + 2 = 28

Let A = Event that a red pen is picked

n(A) = 9 + 4 = 13

\begin{array}{l} P (A) = \frac{n (A)}{n (S)} \\ = \frac{13}{28} \end{array}

Example 2:

A bag contains 45 green cards and yellow cards. A card is picked at random from the bag. The probability that a green card is picked is

\frac{1}{5} .

How many green cards must be added to the bag so that the probability of picking a green card becomes ½?

Solution:

n(S) = 45

Let

x = number of green cards in the bag.

A = Event of randomly picking a green card.

n(A) = x

\begin{array}{l} P (A) = \frac{n (A)}{n (S)} \\ \frac{1}{5} = \frac{x}{45} \\ x = \frac{45}{5} \\ x = 9 \end{array}

Let y is the number of green cards added to the bag.

\frac{9 + y}{45 + y} = \frac{1}{2}

2 (9 + y) = 45 + y

18 + 2y= 45 + y

2y – y = 45 – 18

y = 27

6.2 Quantity Represented by the Area under a Graph (Part 1)

Posted on April 24, 2020 by user

6.2 Quantity Represented by the Area under a Graph (Part 1)

1. In the speed-time graph,

(a) Quantity represented by the gradient of the graph is acceleration or the rate of change of speed.

(b) Quantity represented by the area under the graph is distance.

Example 1:

Calculate the distance of each of the following graphs.

(a)

Distance = Area under the speed-time graph = Area of a triangle

\begin{array}{l} Distance = \frac{1}{2} \times b a s e \times h e i g h t \\ = \frac{1}{2} \times 7 \times 6 = 21 m \end{array}

(b)

Distance = Area under the speed-time graph = Area of a rectangle

Distance = Length × Breadth

= 6 × 4 = 24 m

(c)

Distance = Area under the speed-time graph = Area of a trapezium

\begin{array}{l} Distance = \frac{1}{2} (a + b) h \leftarrow \begin{array}{l} Area of trapezium \\ = \frac{1}{2} \times Sum of the two \\ parallel sides \times Height \end{array} \\ = \frac{1}{2} (4 + 6) \times 8 = 40 m \end{array}