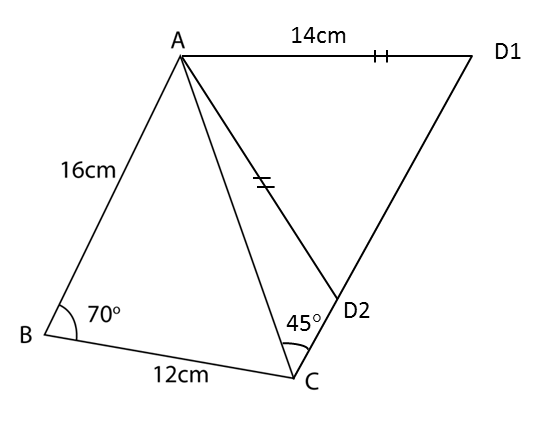
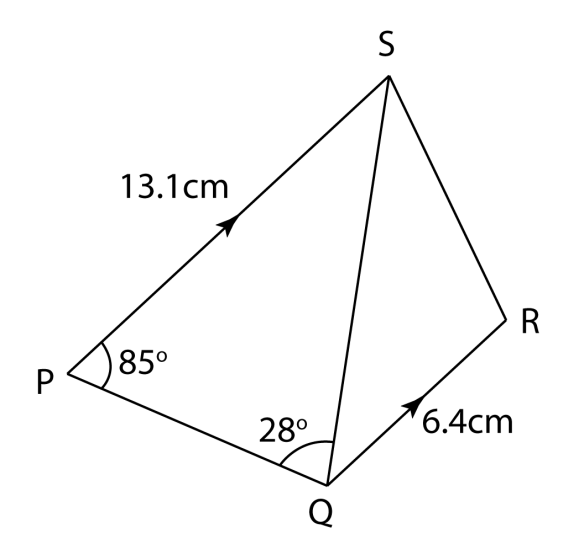
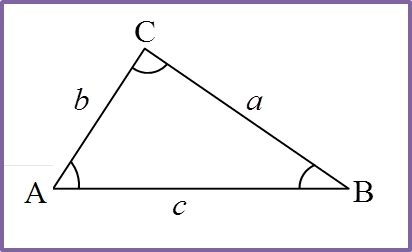
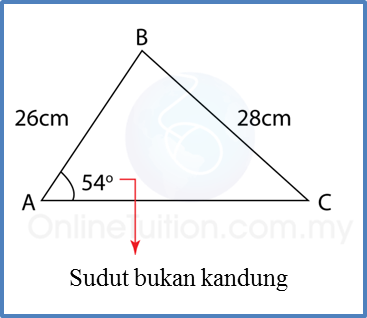
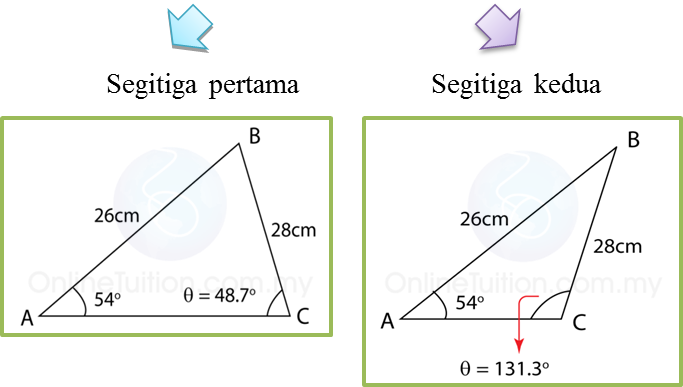
Soalan 10 (10 markah):
Penyelesaian secara lukisan berskala tidak diterima.
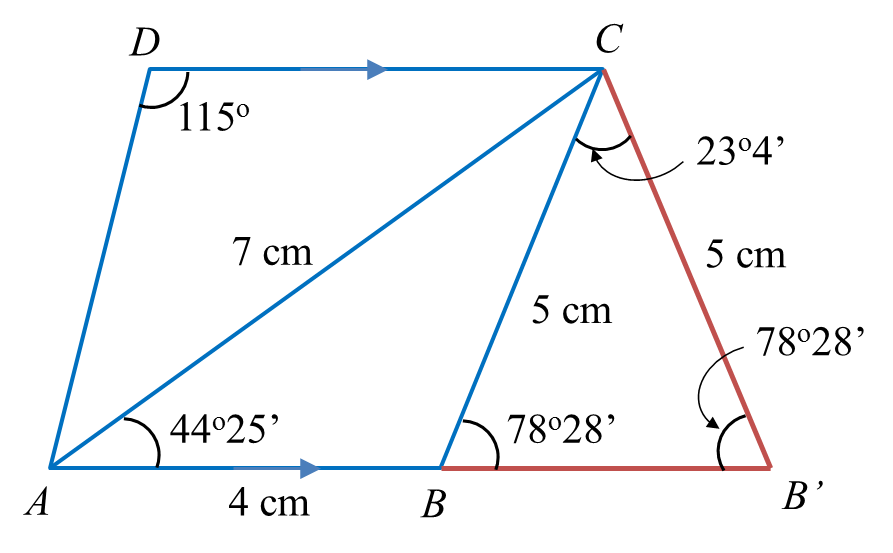
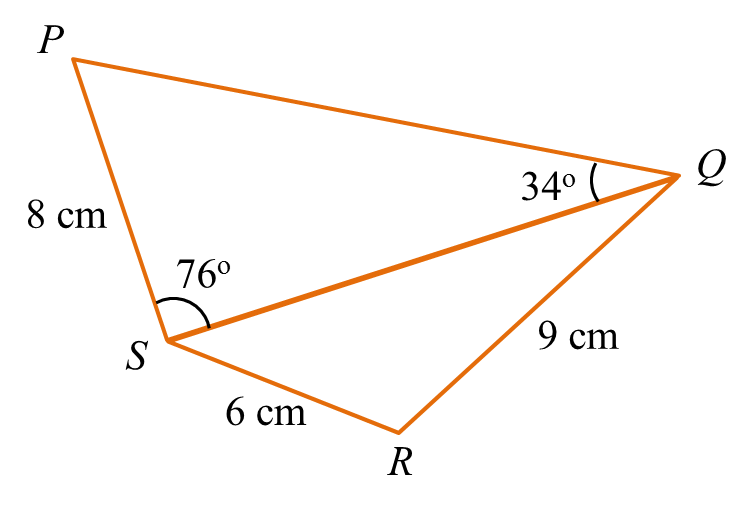
Rajah menunjukkan sisi empat PQRS pada suatu satah mengufuk.

VQSP ialah sebuah piramid dengan keadaan PQ = 12 m dan V adalah 5 m tegak di atas P.
Cari
(a) ∠QSR,
(b) panjang, dalam m, bagi QS,
(c) luas, dalam m2, bagi satah condong QVS.
Penyelesaian:
(a)
(b)
(c)
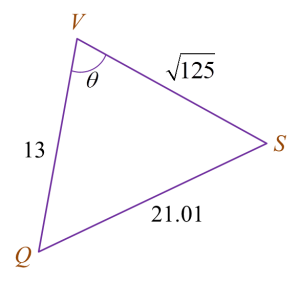
Penyelesaian secara lukisan berskala tidak diterima.
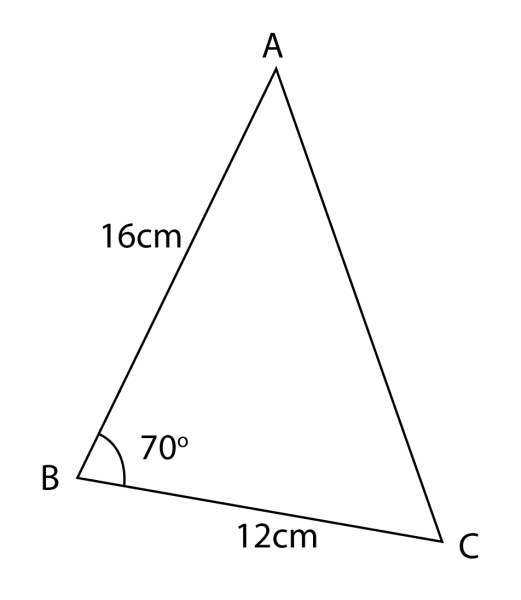
Rajah menunjukkan sisi empat PQRS pada suatu satah mengufuk.

VQSP ialah sebuah piramid dengan keadaan PQ = 12 m dan V adalah 5 m tegak di atas P.
Cari
(a) ∠QSR,
(b) panjang, dalam m, bagi QS,
(c) luas, dalam m2, bagi satah condong QVS.
Penyelesaian:
(a)
(b)
(c)

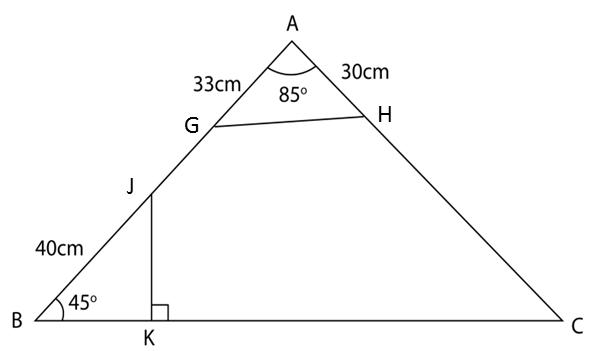
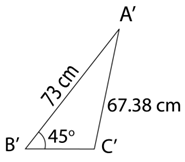
 Diberi bahawa ∠PST = 37o dan ∠TPS = 45o.
Diberi bahawa ∠PST = 37o dan ∠TPS = 45o.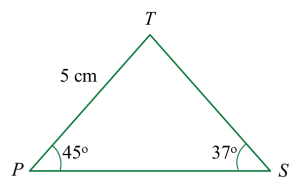
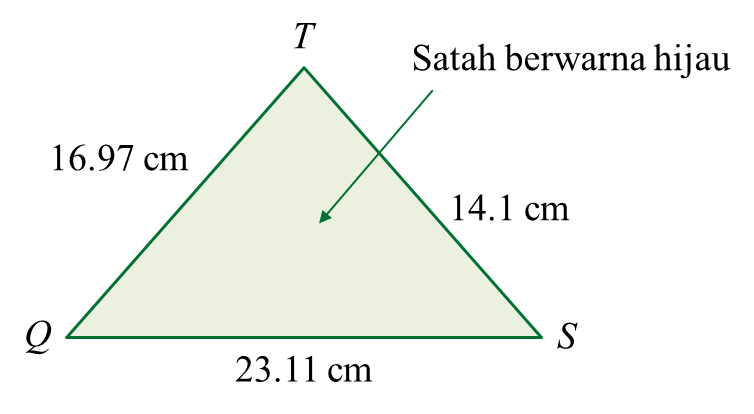
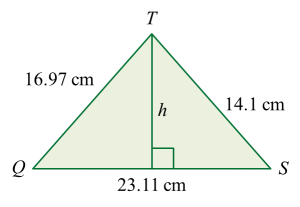

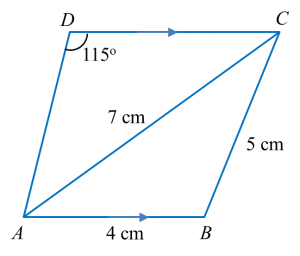 (a) Hitung
(a) Hitung