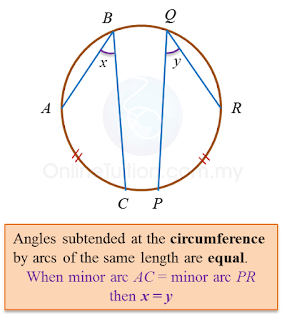
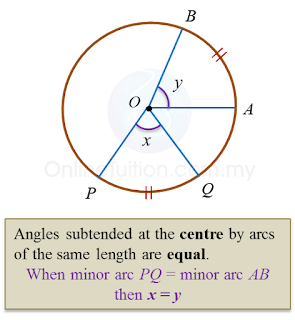
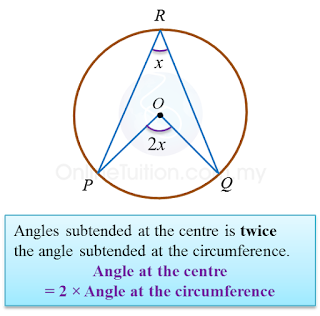
3.2.2 Circles II, PT3 Practice
Question 6:
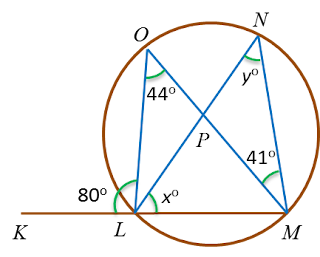
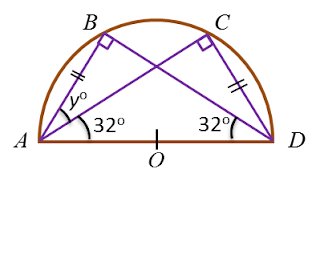
Diagram below shows a circle with centre O. POR is a straight line.
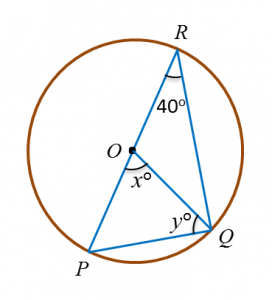

Find the value of x and of y.
Solution:
[adinserter block="5"]
Question 7:
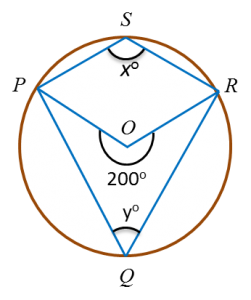
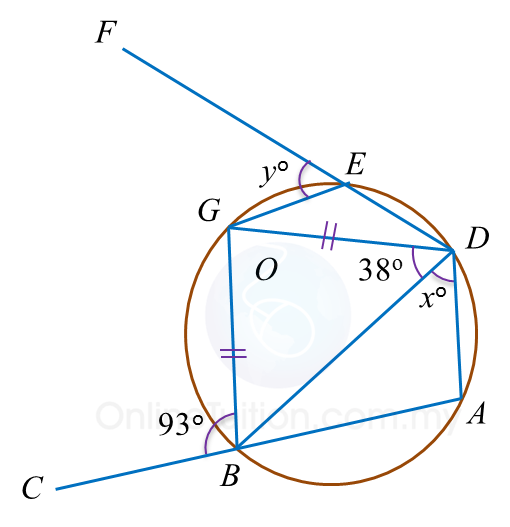
Diagram below shows a circle with centre O.
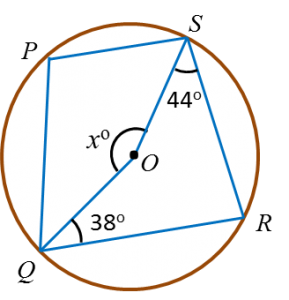
Find the value of x.
Solution:
Diagram below shows a circle with centre O.

Find the value of x.
Solution:
[adinserter block="5"]
Question 8:
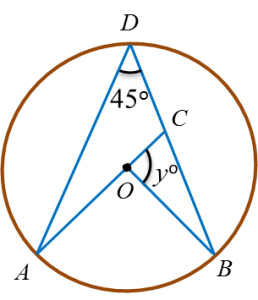
Diagram below shows a circle. QTS is the diameter of the circle and PTR is a straight line.
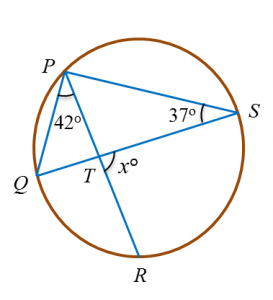 Find the value of x.
Find the value of x.
Solution:
Diagram below shows a circle. QTS is the diameter of the circle and PTR is a straight line.
 Find the value of x.
Find the value of x.Solution:
[adinserter block="5"]
Question 9:
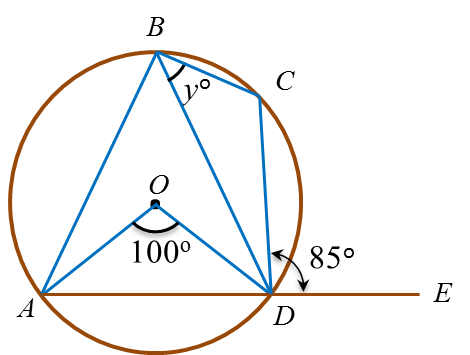
Diagram below shows a circle with centre O. PQR is a straight line.
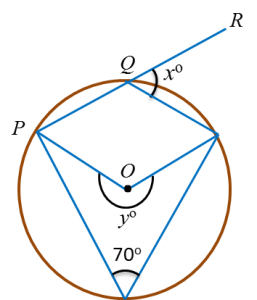
Find the value of x and of y.
Solution:
In cyclic quadrilateral,
Angle at Q = 180o – 70o = 110o
x2 = exterior angle at Q
= 180o – 110o
= 70o
x = 70
yo = reflex angle at O
yo = 360o – (70o × 2)
yo = 220o
y = 220
Diagram below shows a circle with centre O. PQR is a straight line.

Find the value of x and of y.
Solution:
In cyclic quadrilateral,
Angle at Q = 180o – 70o = 110o
x2 = exterior angle at Q
= 180o – 110o
= 70o
x = 70
yo = reflex angle at O
yo = 360o – (70o × 2)
yo = 220o
y = 220
Question 10:
In diagram below, ABCD and DEFG are straight lines.
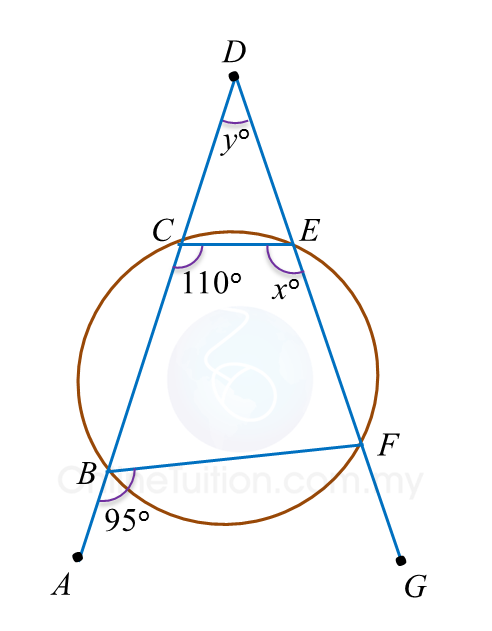 Find the value of x and of y.
Find the value of x and of y.
Solution:
In diagram below, ABCD and DEFG are straight lines.
 Find the value of x and of y.
Find the value of x and of y.Solution: