Question 1:
Evaluate 5 + (–7)
Solution:

Therefore,
5 + (–7) = 5 – 7
= –2
Evaluate 5 + (–7)
Solution:

Therefore,
5 + (–7) = 5 – 7
= –2
Question 2:
Evaluate –6 – (–5)
Solution:

Therefore,
–6 – (–5) = –6 + 5
= –1
Evaluate –6 – (–5)
Solution:

Therefore,
–6 – (–5) = –6 + 5
= –1
Question 3:
Simplify –3 + 7 + (–2)
Solution:
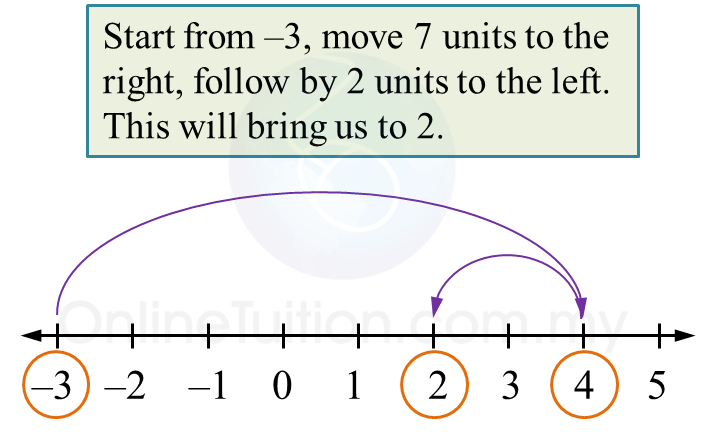
Therefore,
–3 + 7 + (–2) = 4 + (–2)
= 4 – 2
= 2
Simplify –3 + 7 + (–2)
Solution:

Therefore,
–3 + 7 + (–2) = 4 + (–2)
= 4 – 2
= 2
Question 4:
Simplify 5 + (–4) + (–3)
Solution:
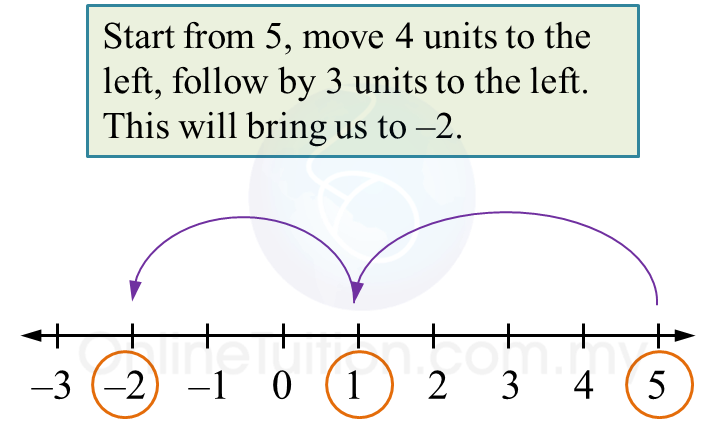
Therefore,
5 + (–4) + (–3)
= 5 – 4 – 3
= –2
Simplify 5 + (–4) + (–3)
Solution:

Therefore,
5 + (–4) + (–3)
= 5 – 4 – 3
= –2

 Therefore,
Therefore, Therefore,
Therefore,