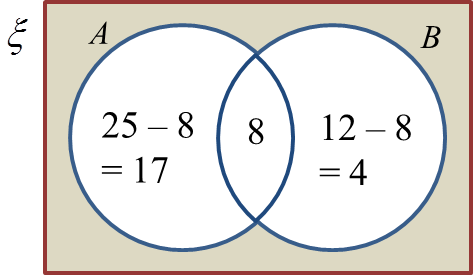Soalan 9 (3 markah):
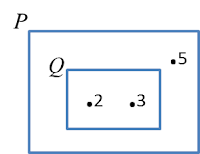
(a) Diberi bahawa set E = {nombor kuasa dua sempurna} dan set F = {9, 16, 25}.
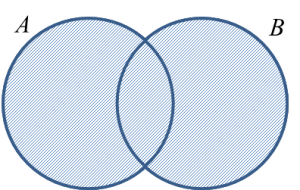
Lengkapkan gambar rajah Venn di ruang jawapan untuk menunjukkan hubungan antara set E dan set F.
Jawapan:

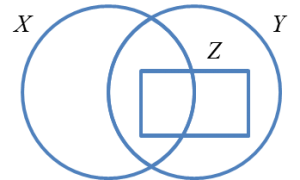
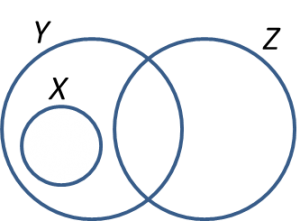
(b) Gambar rajah Venn pada Rajah 1 menunjukkan set X, set Y dan set Z.
Set semesta, ξ = X U Y U Z.

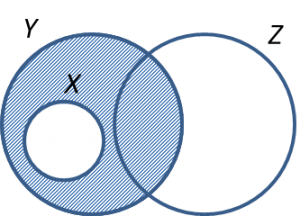
Nyatakan hubungan yang diwakili oleh rantau berlorek di antara set X, set Y dan set Z.
Penyelesaian:
(a)

(b)

Maka, hubungan yang diwakili oleh rantau berlorek di antara set X, set Y dan set Z ialah (X ∩ Y) ∪ Z
(a) Diberi bahawa set E = {nombor kuasa dua sempurna} dan set F = {9, 16, 25}.
Lengkapkan gambar rajah Venn di ruang jawapan untuk menunjukkan hubungan antara set E dan set F.
Jawapan:

(b) Gambar rajah Venn pada Rajah 1 menunjukkan set X, set Y dan set Z.
Set semesta, ξ = X U Y U Z.

Nyatakan hubungan yang diwakili oleh rantau berlorek di antara set X, set Y dan set Z.
Penyelesaian:
(a)

(b)

Maka, hubungan yang diwakili oleh rantau berlorek di antara set X, set Y dan set Z ialah (X ∩ Y) ∪ Z
Soalan 10 (3 markah):
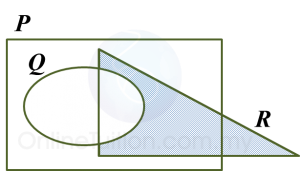
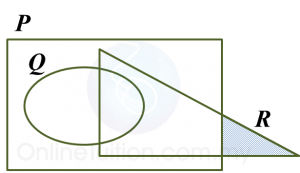
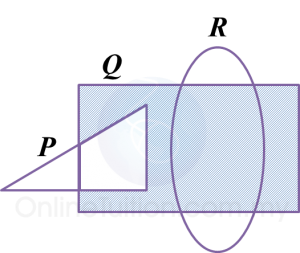
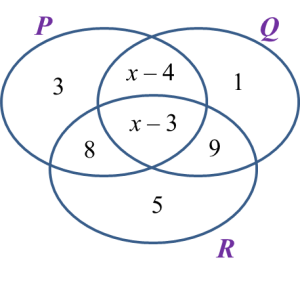
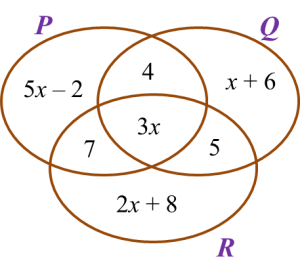
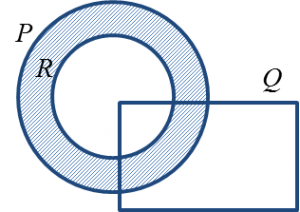
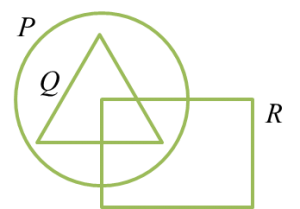
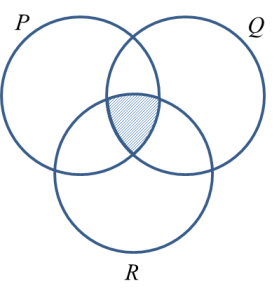
Gambar rajah Venn di ruang jawapan menunjukkan set P, set Q dan set R dengan keadaan set semesta ξ = P U Q U R.
Pada rajah di ruang jawapan, lorek set
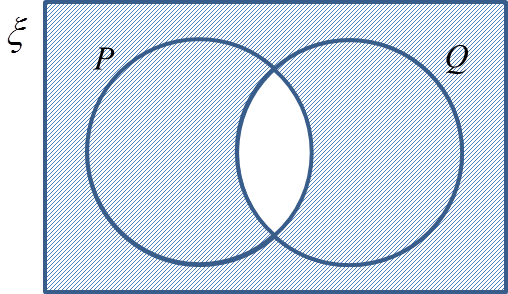
(a) P’,
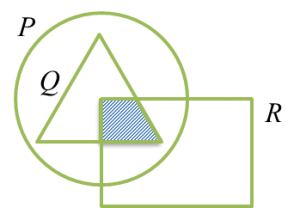
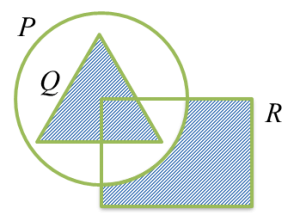
(b) (P ∩ Q) U R
Jawapan:

Penyelesaian:
(a)

(b)

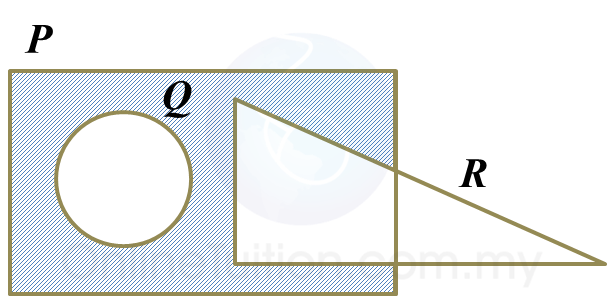
Gambar rajah Venn di ruang jawapan menunjukkan set P, set Q dan set R dengan keadaan set semesta ξ = P U Q U R.
Pada rajah di ruang jawapan, lorek set
(a) P’,
(b) (P ∩ Q) U R
Jawapan:

Penyelesaian:
(a)

(b)