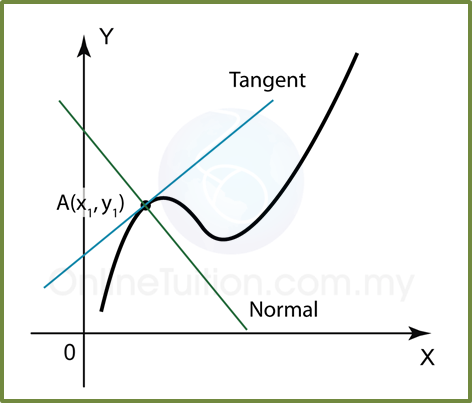
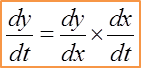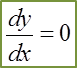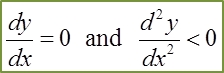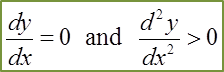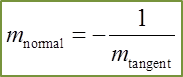Question 20:
Solution:
The volume of water V cm3, in a container is given by
, where h cm is the height of the water in the container. Water is poured into the container at the rate of 15cm3s-1. Find the rate of change of the height of water in cms-1, at the instant when its height is 3cm.
Solution:
Question 21:
Solution:
(a)
(b)
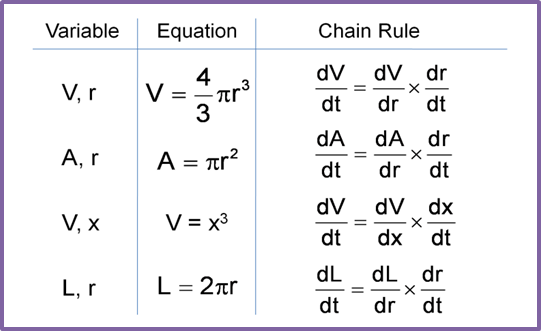
A wire of length 88 cm is bent to form a circle. When the wire is heated, the length increases at the rate of 0.3 cms-1.
(a) Calculate the rate of change in the radius of the circle.
(b) Hence, calculate the radius of the circle after 5s.
(a)
(b)