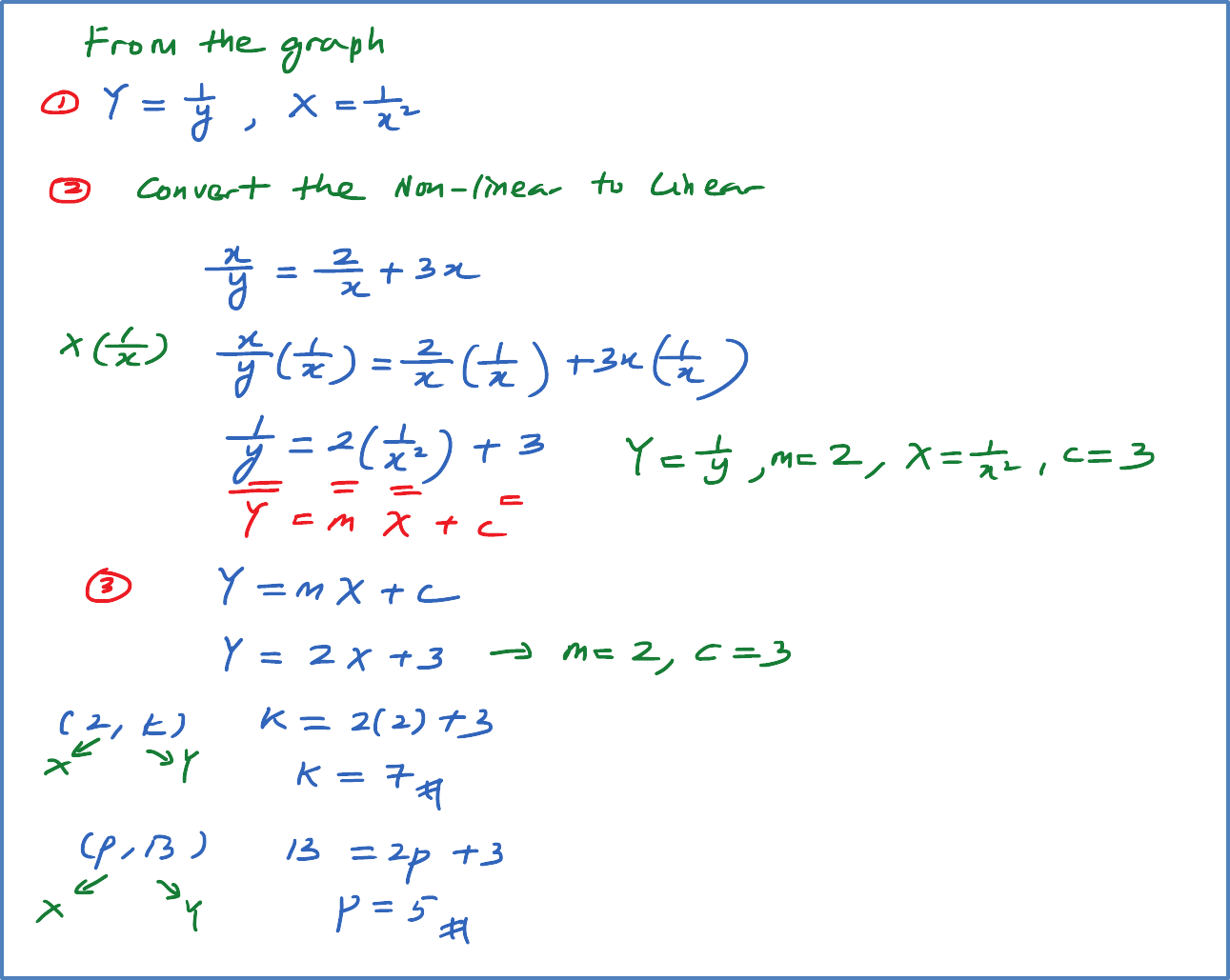Quadratic Equations Long Questions (Question 11 – 13)

Posted on May 25, 2020 by Myhometuition

Question 11:
Solve the following quadratic equation:

\frac{5 x + 3 x^{2}}{1 - 2 x} = 6

Solution:

\begin{array}{l} \frac{5 x + 3 x^{2}}{1 - 2 x} = 6 \\ 5 x + 3 x^{2} = 6 - 12 x \\ 3 x^{2} + 5 x + 12 x - 6 = 0 \\ 3 x^{2} + 17 x - 6 = 0 \\ (3 x - 1) (x + 6) = 0 \\ 3 x - 1 = 0 or x + 6 = 0 \\ 3 x = 1 x = - 6 \\ x = \frac{1}{3} x = - 6 \end{array}

Question 12:

Diagram above shows a rectangle ABCD.

(a) Express the area of ABCD in terms of n.

(b) Given the area of ABCD is 60 cm², find the length of AB.

Solution:

(a)

Area of ABCD

= (n + 7) × n

= (n²+ 7n) cm²

(b)

Given the area of ABCD = 60

n²+ 7n = 60

n²+ 7n – 60 = 0

(n – 5) (n + 12) = 0

n = 5 or n = – 12 (not accepted)

When n = 5,

Length of AB = 5 + 7 = 12 cm

Question 13 (4 marks):
Solve the following quadratic equation:

- \frac{2}{3 x - 5} = \frac{x}{3 x - 1}

Solution:

\begin{array}{l} - \frac{2}{3 x - 5} = \frac{x}{3 x - 1} \\ - 2 (3 x - 1) = x (3 x - 5) \\ - 6 x + 2 = 3 x^{2} - 5 x \\ 3 x^{2} - 5 x + 6 x - 2 = 0 \\ 3 x^{2} + x - 2 = 0 \\ (3 x - 2) (x + 1) = 0 \\ 3 x - 2 = 0 or x + 1 = 0 \\ x = \frac{2}{3} or x = - 1 \end{array}

SPM Practice 2 (Question 8 – 10)

Posted on May 25, 2020 by Myhometuition

Question 8:
The variables x and y are related by the equation $y = \frac{p}{3^{x}}$ , where k is a constant.
Diagram below shows the straight line graph obtained by plotting $\log_{10} y$ ag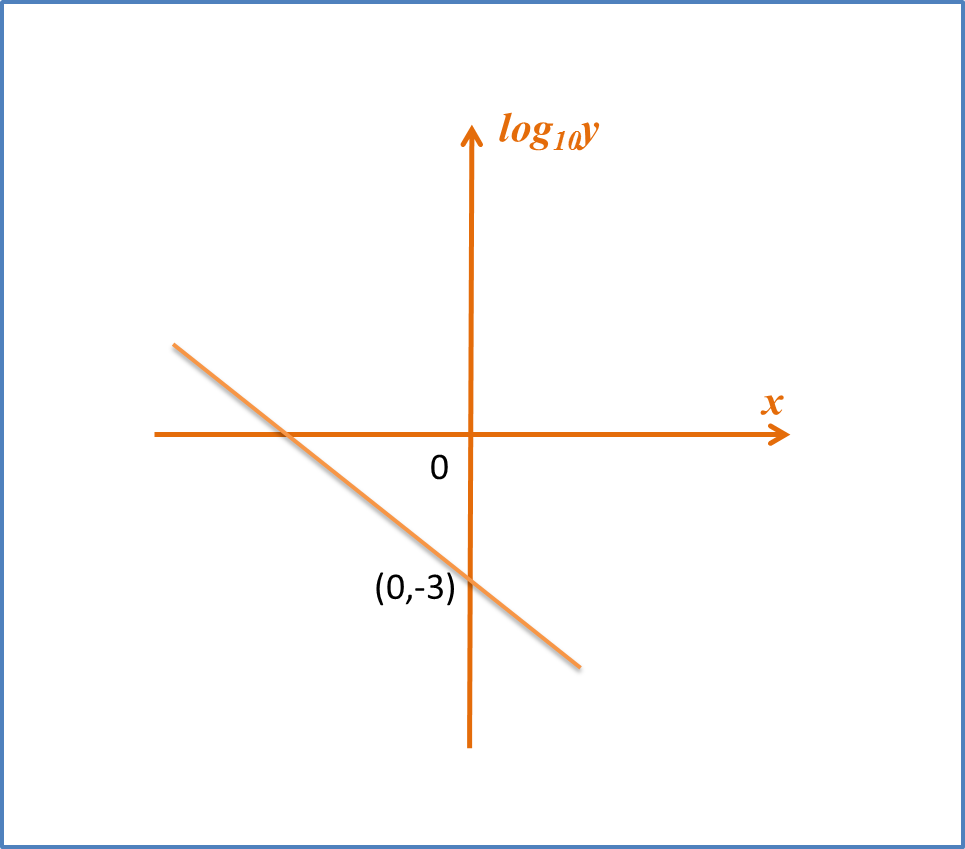ainst x.

Express the equation $y = \frac{p}{3^{x}}$ in its linear form used to obtain the straight line graph shown in Diagram above.
Find the value of p.

Solution: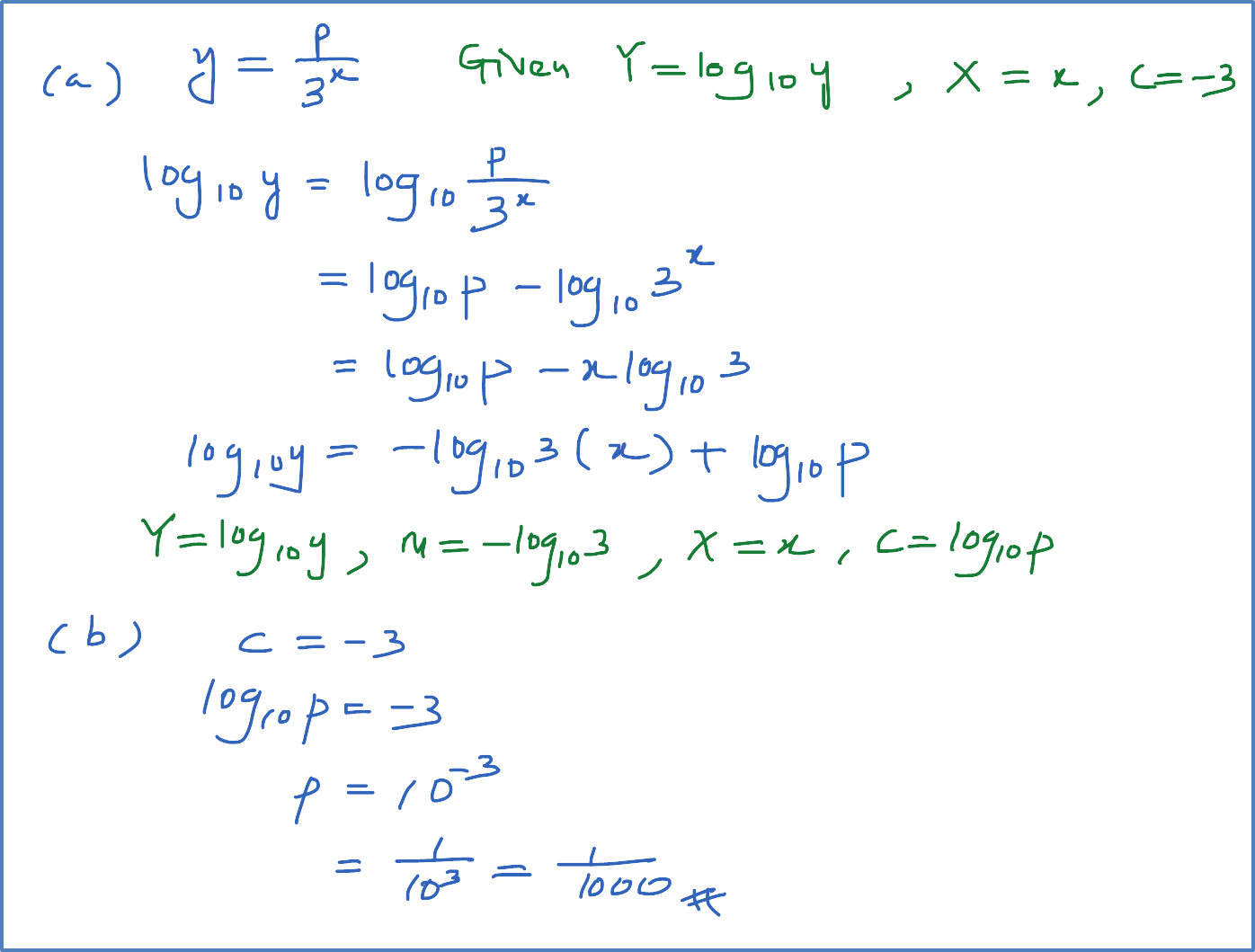

Question 9:
Variable x and y are related by the equation $y^{2} = p x^{q}$ . When the graph lg y against lg x is drawn, the resulting straight line has a gradient of -2 and an vertical intercept of 0.5 . Calculate the value of p and of q.

Solution: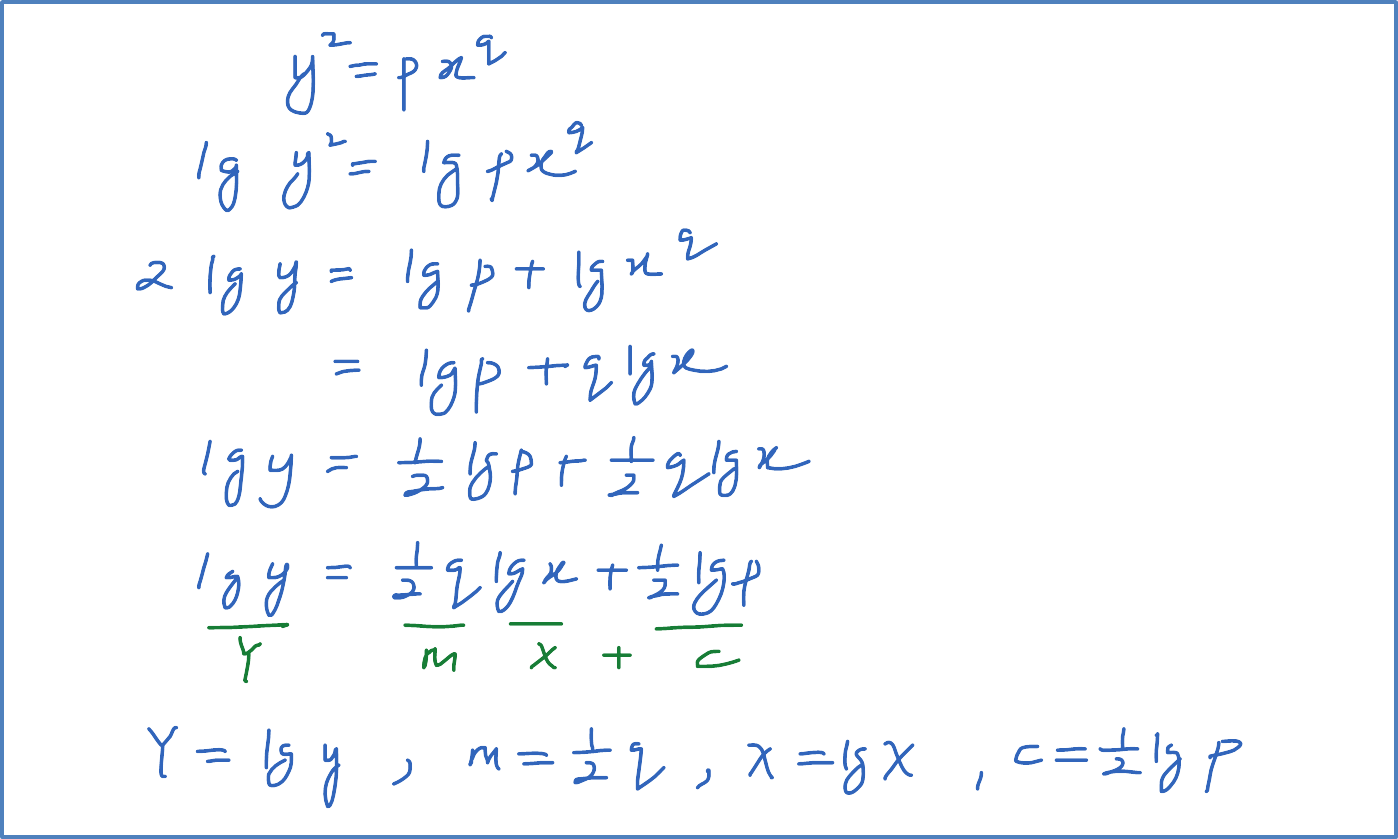

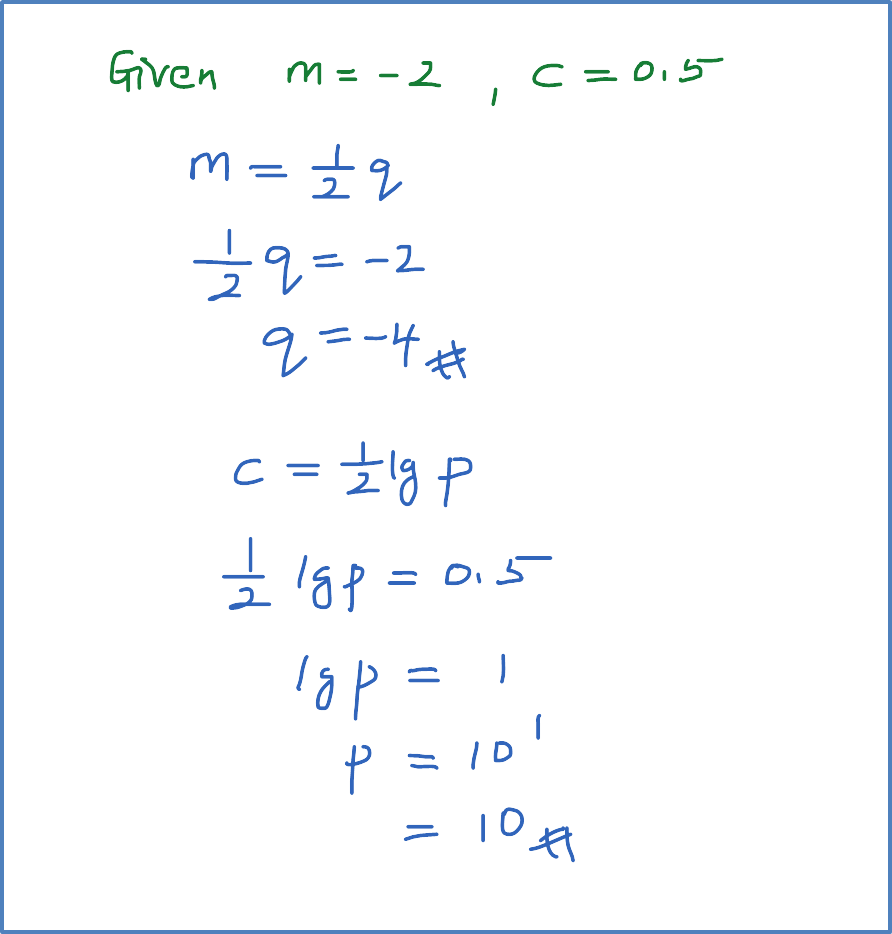
Question 10:
Variable x and y are related by the equation $y = \frac{c}{d - x}$ . When the graph y against xy is drawn the resulting line has gradient 0.25 and an intercept on the y-axis of 1.25. Calculate the value of c and of d.

Solution: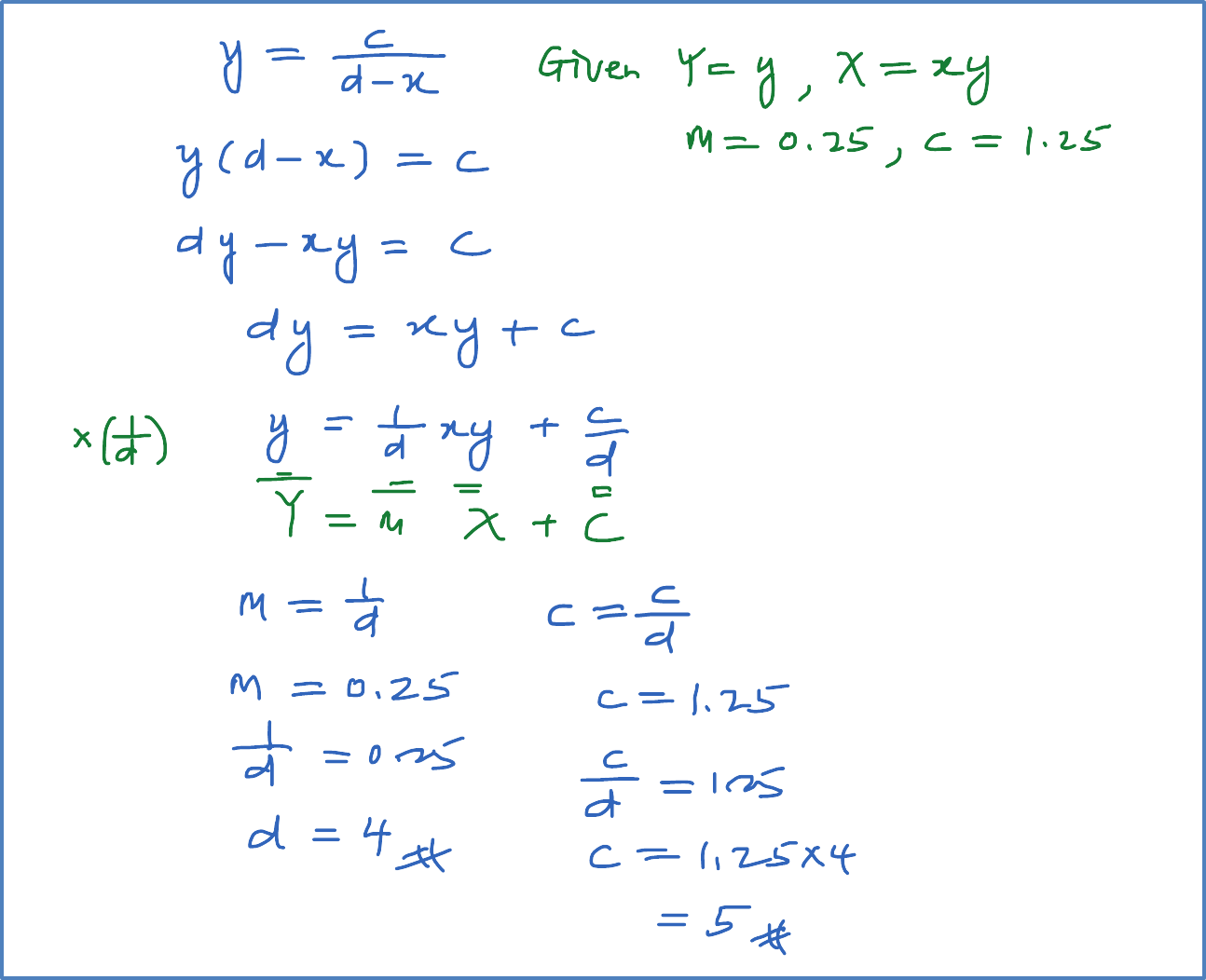

SPM Practice 2 (Question 6 & 7)

Posted on May 25, 2020 by Myhometuition

Question 6:
The variables x and y are related by the equation $y = p x^{3}$ , where p is a constant. Find the value of p and n.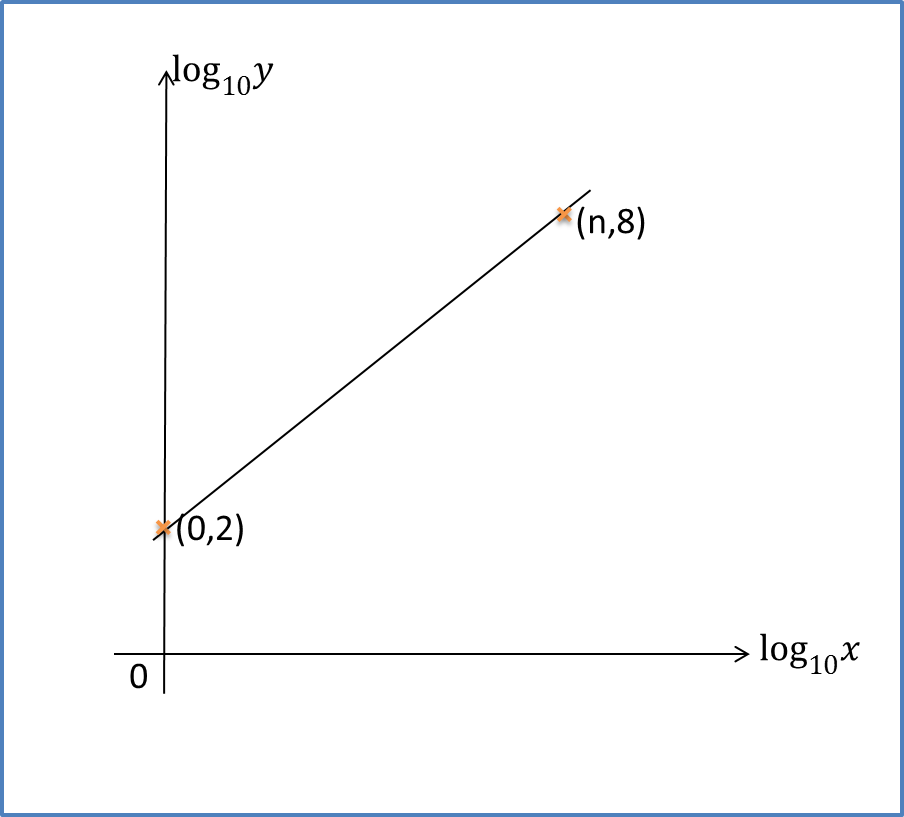

Solution:

Question 7:
Diagram A shows part of the curve $y = a x^{2} + b x$ . Diagram B shows part of the straight line obtained when the equation is reduced to the linear form. Find
(a) the values of a and b,
(b) the values of p and q.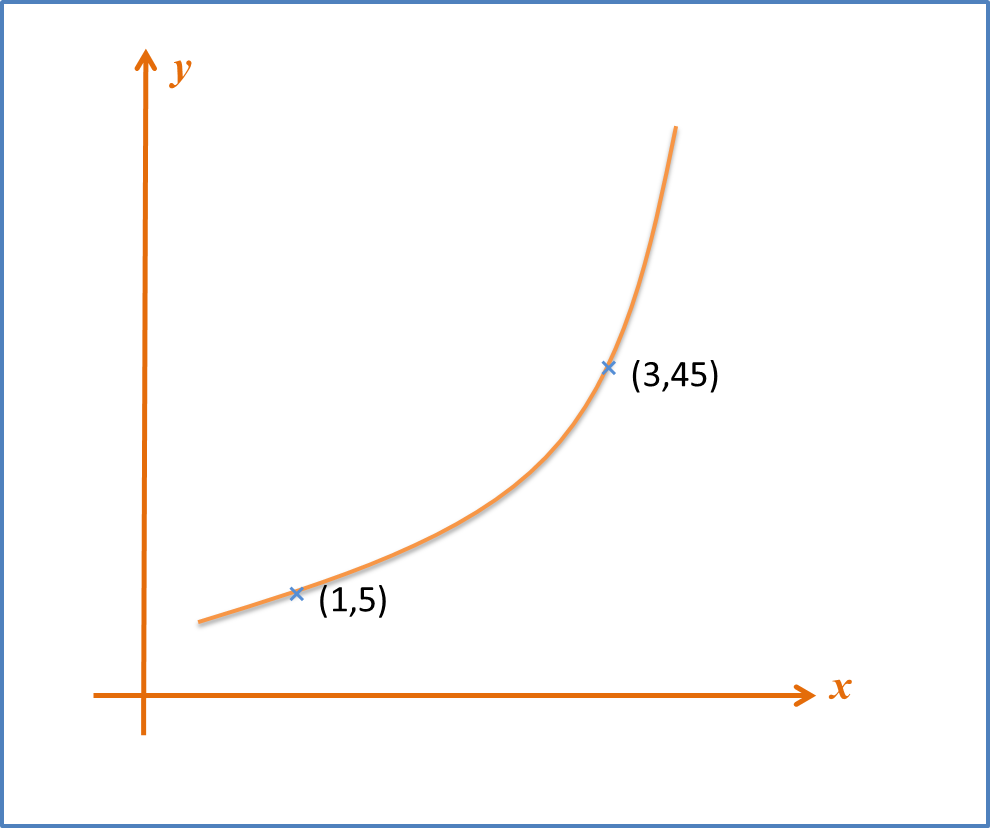

Diagram A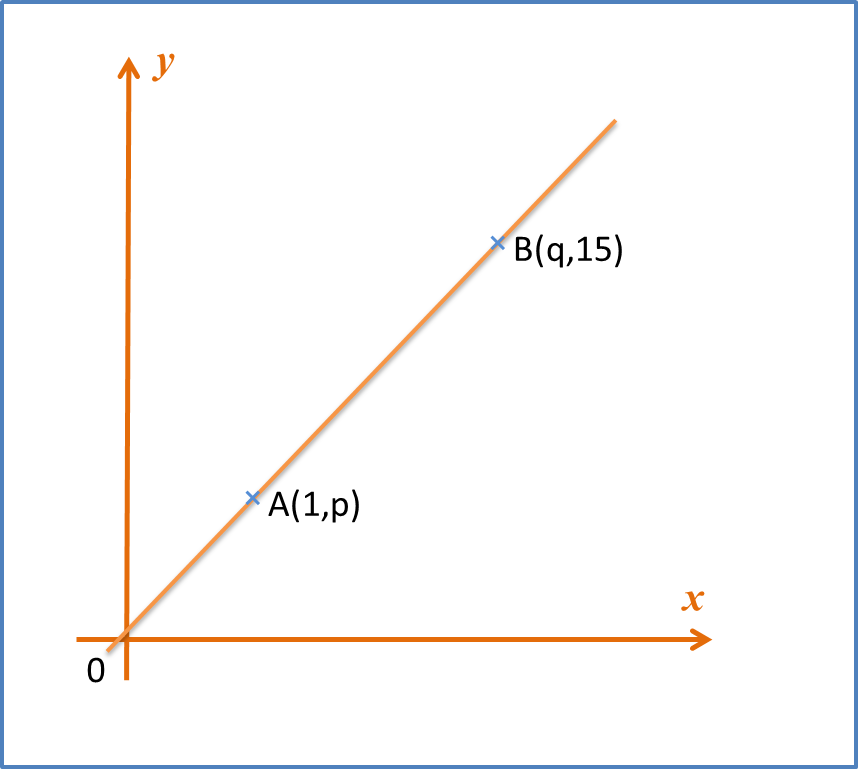

Diagram B

Solution: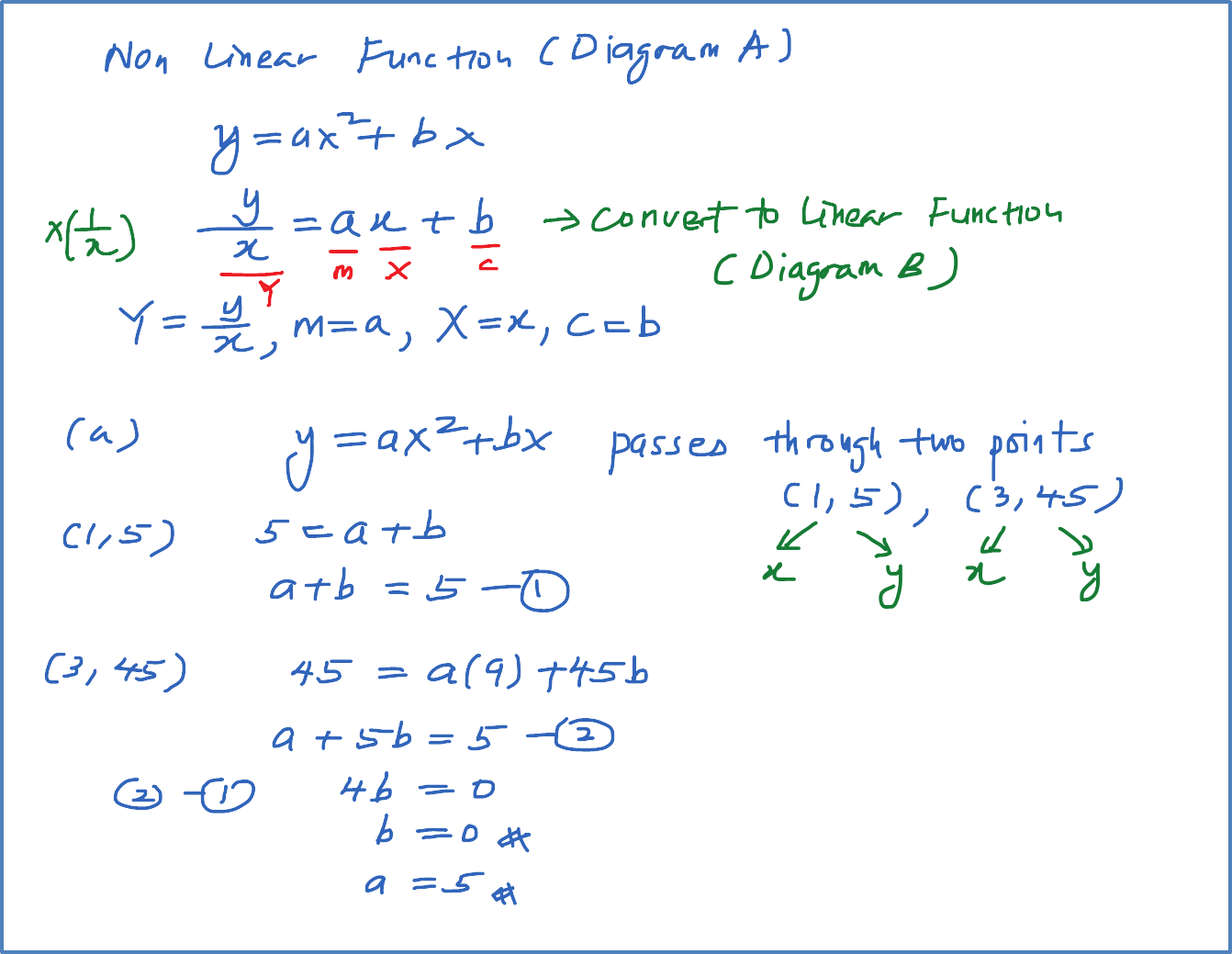

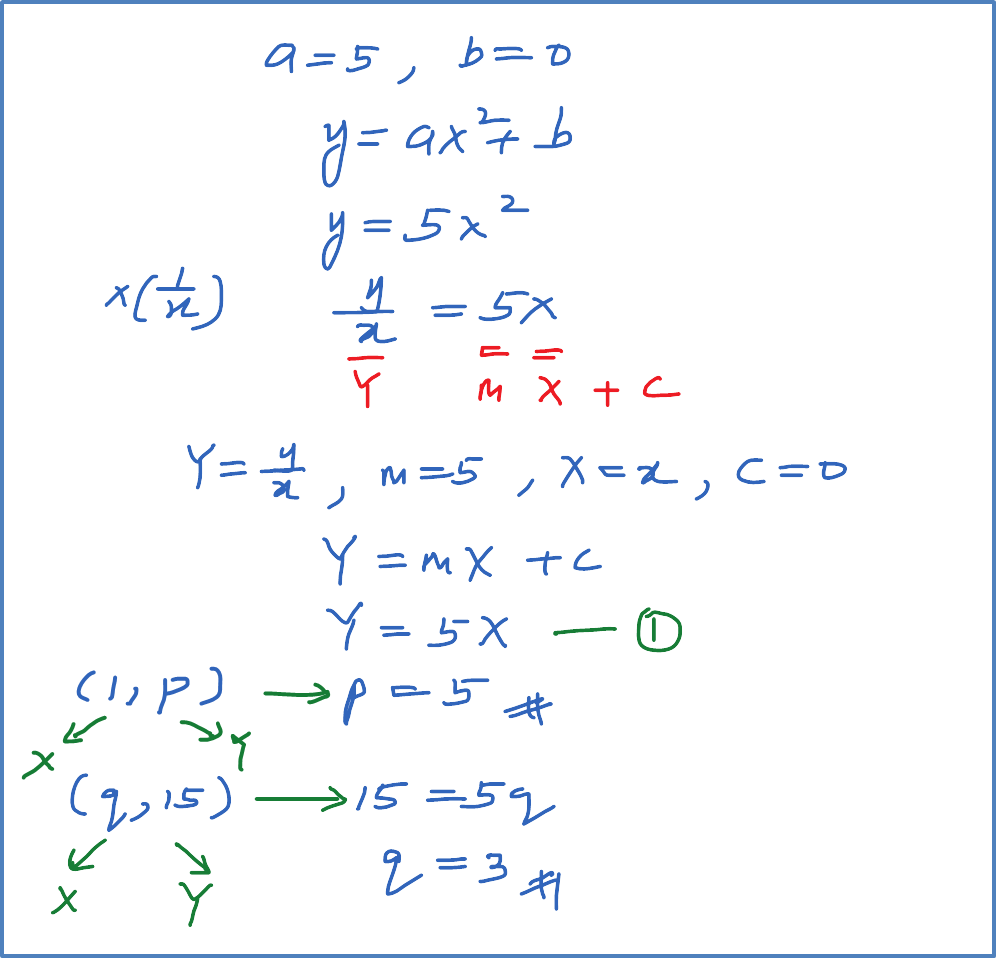
SPM Practice 2 (Question 4 & 5)

Posted on May 25, 2020 by Myhometuition

Question 4:
The diagram shows part of the straight line graph obtained by plotting 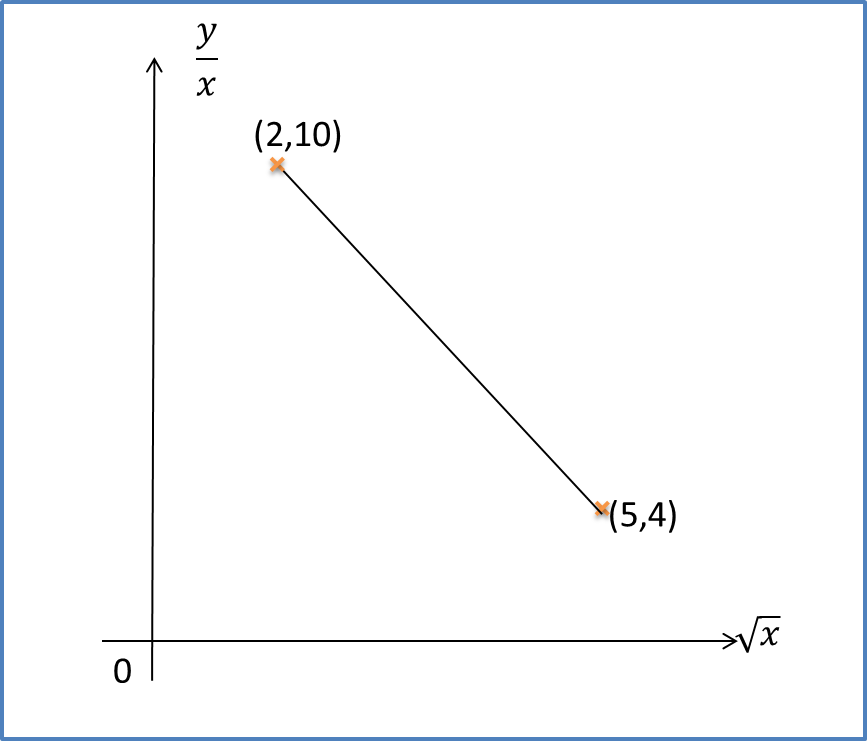$\frac{y}{x}$ against $\sqrt{x}$ .

Given its original non-linear equation is $y = p x + q x^{\frac{3}{2}}$ . Calculate the values of p and q.

Solution:

Question 5:
The diagram below shows the graph of the straight line that is related by the equation 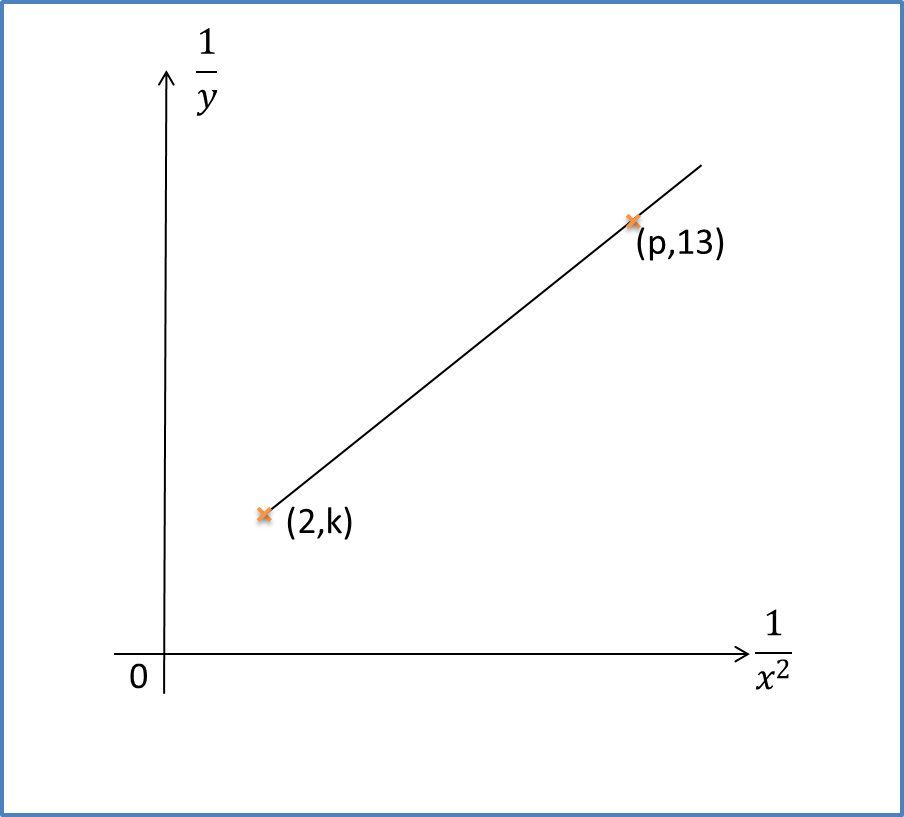$\frac{x}{y} = \frac{2}{x} + 3 x$ .

Find the values of p and k.

Solution:

(G) Sum to Infinity of Geometric Progressions (Part 2)

Posted on May 24, 2020 by Myhometuition

(H) Recurring Decimal

Example of recurring decimal:

\begin{array}{l} \frac{2}{9} = 0.2222222222222..... \\ \frac{8}{33} = 0.242424242424..... \\ \frac{41}{333} = 0.123123123123..... \end{array}

Recurring decimal can be changed to fraction using the sum to infinity formula:

S \infty = \frac{a}{1 - r}

Example (Change recurring decimal to fraction)

Express each of the following recurring decimals as a fraction in its lowest terms.

(a) 0.8888 ...

(b) 0.171717...

(c) 0.513513513 ….

Solution:

(a)

0.8888 = 0.8 + 0.08 + 0.008 +0.0008 + ….. (recurring decimal)

\begin{array}{l} G P, a = 0.8, r = \frac{0.08}{0.8} = 0.1 \\ S_{\infty} = \frac{a}{1 - r} \\ S_{\infty} = \frac{0.8}{1 - 0.1} \\ S_{\infty} = \frac{0.8}{0.9} \\ S_{\infty} = \frac{8}{9} \to \begin{array}{l} check using calculator \\ \frac{8}{9} = 0.888888.... \end{array} \end{array}

(b)

0.17171717 …..

= 0.17 + 0.0017 + 0.000017 + 0.00000017 + …..

\begin{array}{l} G P, a = 0.17, r = \frac{0.0017}{0.17} = 0.01 \\ S_{\infty} = \frac{a}{1 - r} \\ S_{\infty} = \frac{0.17}{1 - 0.01} = \frac{0.17}{0.99} = \frac{17}{99} \to \begin{array}{l} remember to check the \\ answer using calculator \end{array} \end{array}

(c)

0.513513513…..

= 0.513 + 0.000513 + 0.000000513 + …..

\begin{array}{l} G P, a = 0.513, r = \frac{0.00513}{0.513} = 0.001 \\ S_{\infty} = \frac{a}{1 - r} \\ S_{\infty} = \frac{0.513}{1 - 0.001} = \frac{0.513}{0.999} = \frac{513}{999} = \frac{19}{37} \end{array}

3. The nth Term of Geometric Progressions (Part 2)

Posted on May 24, 2020 by Myhometuition

(D) The Number of Term of a Geometric Progression

Smart TIPS: You can find the number of term in an arithmetic progression if you know the last term

Example 2:
Find the number of terms for each of the following geometric progressions.

(a) 2, 4, 8, ….., 8192

(b) $\frac{1}{4}, \frac{1}{6}, \frac{1}{9}, ....., \frac{16}{729}$

(c) $- \frac{1}{2}, 1, - 2, ....., 64$

Solution:
(a)

\begin{array}{l} 2, 4, 8, ....., 8192 \leftarrow (Last term is given) \\ a = 2 \\ r = \frac{T_{2}}{T_{1}} = \frac{4}{2} = 2 \\ T_{n} = 8192 \\ a r^{n - 1} = 8192 \leftarrow (T h e n th term of GP, T_{n} = a r^{n - 1}) \\ (2) {(2)}^{n - 1} = 8192 \\ 2^{n - 1} = 4096 \\ 2^{n - 1} = 2^{12} \\ n - 1 = 12 \\ n = 13 \end{array}

(b)

\begin{array}{l} \frac{1}{4}, \frac{1}{6}, \frac{1}{9}, ....., \frac{16}{729} \\ a = \frac{1}{4}, r = \frac{\frac{1}{6}}{\frac{1}{4}} = \frac{2}{3} \\ T_{n} = \frac{16}{729} \\ a r^{n - 1} = \frac{16}{729} \\ (\frac{1}{4}) {(\frac{2}{3})}^{n - 1} = \frac{16}{729} \\ {(\frac{2}{3})}^{n - 1} = \frac{16}{729} \times 4 \\ {(\frac{2}{3})}^{n - 1} = \frac{64}{729} \\ {(\frac{2}{3})}^{n - 1} = {(\frac{2}{3})}^{6} \\ ∴ n - 1 = 6 \\ n = 7 \end{array}

(c)

\begin{array}{l} - \frac{1}{2}, 1, - 2, ....., 64 \\ a = - \frac{1}{2}, r = \frac{- 2}{1} = - 2 \\ T_{n} = 64 \\ a r^{n - 1} = 64 \\ (- \frac{1}{2}) {(- 2)}^{n - 1} = 64 \\ {(- 2)}^{n - 1} = 64 \times - 2 \\ {(- 2)}^{n - 1} = - 128 \\ {(- 2)}^{n - 1} = {(- 2)}^{7} \\ n - 1 = 7 \\ n = 8 \end{array}

(E) Three consecutive terms of a geometric progression

If e, f and g are 3 consecutive terms of GP, then

\frac{g}{f} = \frac{f}{e}

Example 3:

If p + 20, p − 4, p −20 are three consecutive terms of a geometric progression, find the value of p.

Solution:

\begin{array}{l} \frac{p - 20}{p - 4} = \frac{p - 4}{p + 20} \\ (p + 20) (p - 20) = (p - 4) (p - 4) \\ p^{2} - 400 = p^{2} - 8 p + 16 \\ 8 p = 416 \\ p = 52 \end{array}

SPM Practice Question 13 – 15

Posted on May 24, 2020 by Myhometuition

Question 13:
An arithmetic progression consists of 10 terms. The sum of the last 5 terms is 5 and the fourth term is 9. Find the sum of this progression.

Solution:

Question 14:
The sum of the first 6 terms of an arithmetic progression is 39 and the sum of the next 6 terms is –69. Find
(a) The first term and the common difference.
(b) The sum of all the terms from the 15th term to the 25th term.

Solution:

Question 15:
An arithmetic progression has 9 terms. The sum of the first four terms is 24 and the sum of all the odd number terms is 55. Find
(a) The first term and common difference,
(b) The seventh term.

Solution:

SPM Practice Question 4 – 6

Posted on May 24, 2020 by Myhometuition

Question 4:
It is given that -7, h, k, 20,… are the first four terms of an arithmetic progression. Find the value of h and of k.

Solution:

Question 5:
51, 58, 65,... 191 are the first n terms of an arithmetic progression. Find the value of n.

Solution:

Question 6:
Find the number of the multiples of 8 between 100 and 300.

Solution:

The nth Term of Arithmetic Progression (Example 3 & 4)

Posted on May 24, 2020 by Myhometuition

Example 3:
The volume of water in a tank is 75 litres on the first day. Subsequently, 15 litres of water is added to the tank everyday.
Calculate the volume, in litres, of water in the tank at the end of the 12th day.

Solution:

Volume of water on the first day = 75l

Volume of water on the second day = 75 + 15 = 90l

Volume of water on the third day = 90 + 15 = 105l

75, 90, 105, …..

AP, a = 75, d = 90 – 75 = 15

Volume of water on the 12^th day,

T₁₂ = a + 11d

T₁₂ = 75 + 11 (15)

T₁₂ = 240l

Example 4:

The first three terms of an arithmetic progression are 72, 65 and 58.

The nth term of this progression is negative.

Find the least value of n.

Solution:

72, 65, 58

AP, a = 72, d = 65 – 72 = –7

The nth term is negative,

T_n< 0

a + (n – 1) d < 0

72 + (n – 1) (–7) < 0

(n – 1) (–7) < –72

n – 1 > –72/ –7

n – 1 > 10.28

n > 11.28

n must be integer, n = 12, 13, 14, ….

Therefore, the least value of n = 12.

9.2.1 First Derivative for Polynomial Function (Examples)

Posted on May 24, 2020 by Myhometuition

Example:

Find

\frac{d y}{d x}

for each of the following functions:

(a) y = 12

(b) y = x⁴

(c) y = 3x

(d) y = 5x³

\begin{array}{l} (e) y = \frac{1}{x} \\ (f) y = \frac{2}{x^{4}} \\ (g) y = \frac{2}{5 x^{2}} \\ (h) y = 3 \sqrt{x} \\ (i) y = 4 \sqrt{x^{3}} \end{array}

Solution:

(a)
y = 12

\frac{d y}{d x} = 0

(b)
y = x⁴

\frac{d y}{d x}

= 4x³

(c)
y = 3x

\frac{d y}{d x}

= 3

(d)
y = 5x³

\frac{d y}{d x}

= 3(5x²) = 15x²

(e)

\begin{array}{l} y = \frac{1}{x} = x^{- 1} \\ \frac{d y}{d x} = - x^{- 1 - 1} = - \frac{1}{x^{2}} \end{array}

(f)

\begin{array}{l} y = \frac{2}{x^{4}} = 2 x^{- 4} \\ \frac{d y}{d x} = - 4 (2 x^{- 4 - 1}) = - 8 x^{- 5} = - \frac{8}{x^{5}} \end{array}

(g)

\begin{array}{l} y = \frac{2}{5 x^{2}} = \frac{2 x^{- 2}}{5} \\ \frac{d y}{d x} = - 2 (\frac{2 x^{- 2 - 1}}{5}) = - \frac{4 x^{- 3}}{5} = - \frac{4}{5 x^{3}} \end{array}

(h)

\begin{array}{l} y = 3 \sqrt{x} = 3 {(x)}^{\frac{1}{2}} \\ \frac{d y}{d x} = \frac{1}{2} (3 x^{\frac{1}{2} - 1}) = \frac{3}{2} x^{- \frac{1}{2}} = \frac{3}{2 \sqrt{x}} \end{array}

(i)

\begin{array}{l} y = 4 \sqrt{x^{3}} = 4 {(x^{3})}^{\frac{1}{2}} = 4 x^{\frac{3}{2}} \\ \frac{d y}{d x} = \frac{3}{2} (4 x^{\frac{3}{2} - 1}) = 6 x^{\frac{1}{2}} = 6 \sqrt{x} \end{array}