10.2.3 Circles I, PT3 Focus Practice

Question 11:
The Town Council plans to build an equilateral triangle platform in the middle of a roundabout. The diameter of circle RST is 24 m and the perpendicular distance from R to the line ST is 18 m. as shown in Diagram below.
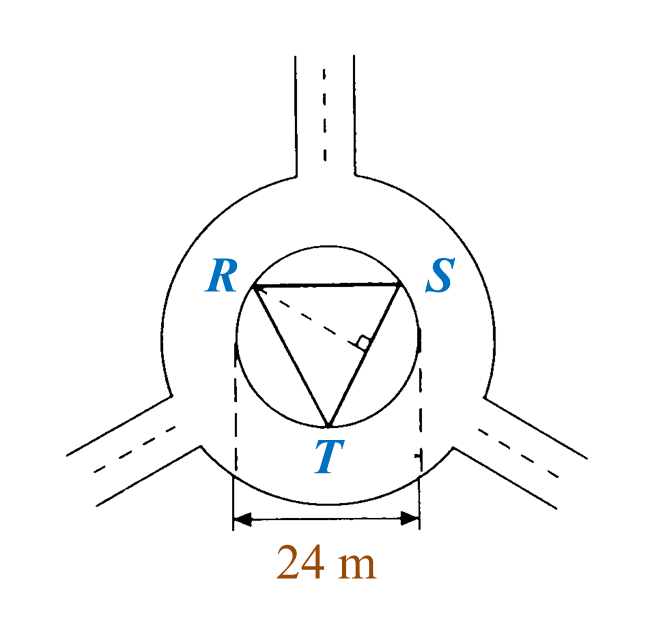Find the perimeter of the platform.

Solution:

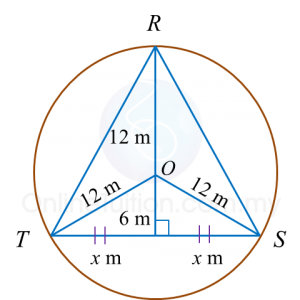
Given diameter = 24 m
hence radius = 12 m
O is the centre of the circle.
Using Pythagoras’ theorem:
$\begin{array}{l}{x}^2={12}^2-6^2\\ x=\sqrt{144-36}\\ =10.39\text{ m}\\ TS=RS=RT\\ =10.39\text{ m }\times 2\\ =20.78\text{ m}\\ \text{Perimeter of the platform}\\ TS+RS+RT\\ =20.78\times 3\\ =63.34\text{ m}\end{array}$

Question 12:
Amy will place a ball on top of a pillar in Diagram below. Table below shows the diameters of three balls X, Y and Z.


Which ball X, Y or Z, can fit perfectly on the top of the pillar? Show the calculation to support Amy’s choice.

Solution:

$\begin{array}{l}\text{Let the radius of the top of the pillar}=r\text{ cm}\text{.}\\ O\text{ is the centre of the circle}\text{.}\\ \text{In }\Delta OQR,\\ r^2={\left(r-4\right)}^2+8^2\left(\text{using Pythagoras' theorem}\right)\\ r^2=r^2-8r+16+64\\ r^2=r^2-8r+80\\ r^2-r^2+8r=80\\ 8r=80\\ r=\frac{80}{8}\\ r=10\text{ cm}\\ \\ \text{Therefore, diameter}\\ =2\times 10\\ =20\text{ cm}\\ \\ \text{Ball }Y\text{ with diameter 20 cm can fit perfectly }\\ \text{on top of the pillar}\text{.}\end{array}$

Question 13:
Diagram below shows a rim of a bicycle wheel with a diameter of 26 cm. Kenny intends to build a holder for the rim.

Which of the rim holder, X, Y or Z, can fit the bicycle rim perfectly? Show the calculation to support your answer.

Solution:

$\begin{array}{l}\text{Let the radius of the rim holder}=r\text{ cm}\text{.}\\ O\text{ is the centre of the circle}\text{.}\\ \text{In }\Delta OQR,\\ r^2={\left(r-8\right)}^2+{12}^2\left(\text{using Pythagoras' theorem}\right)\\ r^2=r^2-16r+64+144\\ r^2=r^2-16r+208\\ r^2-r^2+16r=208\\ 16r=208\\ r=\frac{208}{16}\\ r=13\text{ cm}\\ \\ \text{Therefore, diameter}\\ =2\times 13\\ =26\text{ cm}\\ \\ \text{Rim holder }Z\text{ with diameter 26 cm can fit the bicycle perfectly}\text{.}\end{array}$