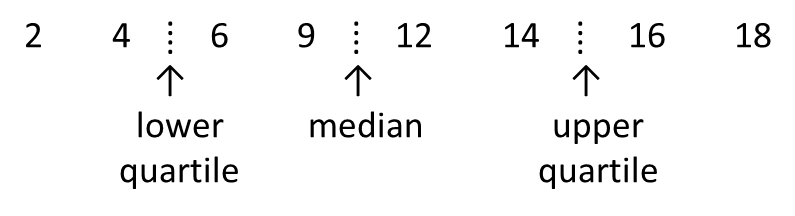
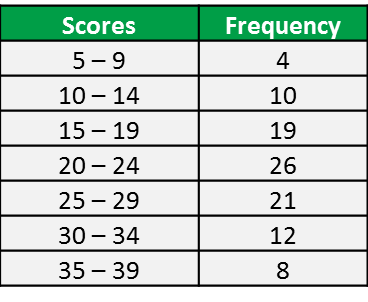
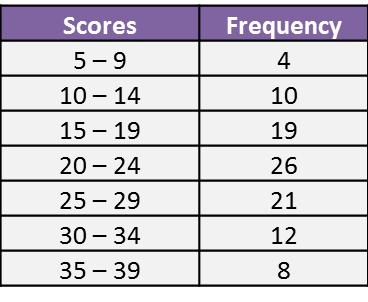
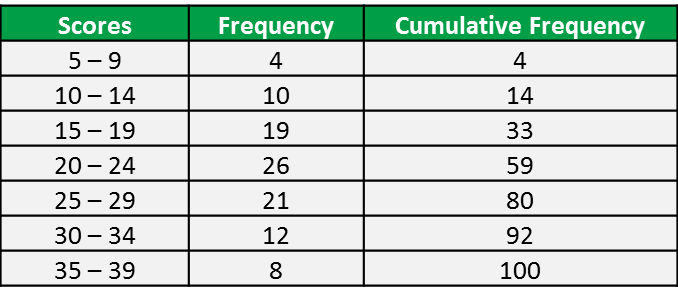
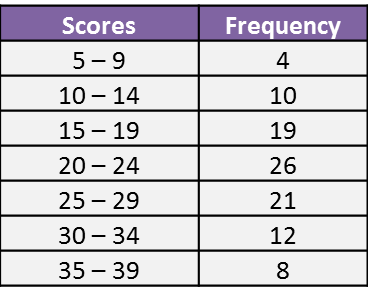
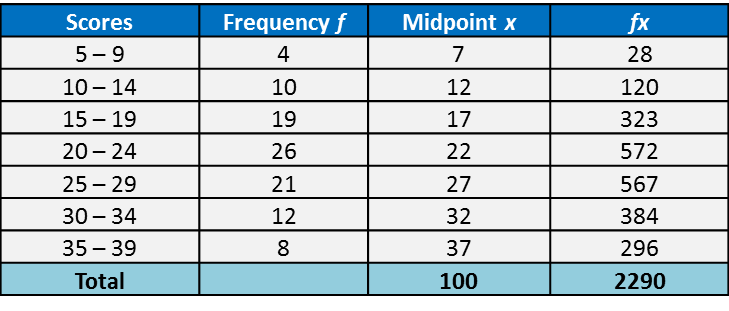
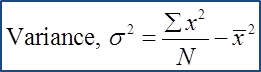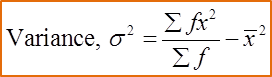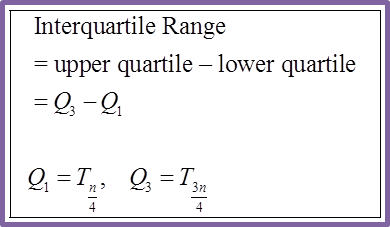Question 1:
Solution:
Given that the standard deviation of five numbers is 6 and the sum of the squares of these five numbers is 260. Find the mean of this set of numbers.
Solution:
Question 2:
Both of the mean and the standard deviation of 1, 3, 7, 15, m and n are 6. Find
Both of the mean and the standard deviation of 1, 3, 7, 15, m and n are 6. Find
(a) the value of m + n,
(b) the possible values of n.
Solution:
(a)1 + 3 + 7 + 15 + m + n= 36
26 + m + n= 36
m + n = 10
(b)