Yearly Archives: 2020
Domain, Range, Objects, Images and Absolute Value Functions
(B) Domain, Range, Objects and Images of a Function
Example:

The arrow diagram above represents the function f : x → 2x2 – 5. State
(a) the domain,
(b) the range,
(c) the image of –2,
(d) the objects of
(i) –3,
(ii) –5.
Solution:
(a) Domain = {–2, –1, 0, 1, 2}.
(b) Range = {–5, –3, 3}.
(c) The image of –2 is 3.
(d) (i) The objects of –3 are 1 and –1.
(d) (ii) The objects of –5 is 0.
Example:

The arrow diagram above represents the function f : x → 2x2 – 5. State
(a) the domain,
(b) the range,
(c) the image of –2,
(d) the objects of
(i) –3,
(ii) –5.
Solution:
(a) Domain = {–2, –1, 0, 1, 2}.
(b) Range = {–5, –3, 3}.
(c) The image of –2 is 3.
(d) (i) The objects of –3 are 1 and –1.
(d) (ii) The objects of –5 is 0.
(C) Absolute Value Functions
1. Symbol | | is read as ‘the modulus’ of a number. In general, the modulus of x, that is | x |, is defined as
2. In other words, modulus of a number always positive.
3. The absolute value function | f(x) | is defined by
Solution:
(a)
Given f (x) = |x + 2|
Image of –4 is f(–4) = | –4 + 2| = | –2| = 2
Image of –3 is f(–3) = | –3 + 2| = | –1| = 1
Image of 0 is f(0) = | 0 + 2| = | 2 | = 2
Image of 2 is f(2) = | 2 + 2| = | 4 | = 4
(b)
From (a),
f(–4) = 2
f(–3) = 1
f(0) = 2
f(2) = 4
Determine the point where the graph touches the x-axis.
At x-axis, f (x) = 0
|x + 2| = 0
x + 2 = 0
x = –2

Therefore, range of values of f (x) is 0 ≤ f (x) ≤ 4.
1. Symbol | | is read as ‘the modulus’ of a number. In general, the modulus of x, that is | x |, is defined as
2. In other words, modulus of a number always positive.
3. The absolute value function | f(x) | is defined by
Example:
Given function f : x → |x + 2|.
(a) Find the image of –4, –3, 0 and 2.
(b) Sketch the graph of f (x) for the domain –4 ≤ x ≤ 2.
Hence, state the range of values of f (x) based on the given domain.
Solution:
(a)
Given f (x) = |x + 2|
Image of –4 is f(–4) = | –4 + 2| = | –2| = 2
Image of –3 is f(–3) = | –3 + 2| = | –1| = 1
Image of 0 is f(0) = | 0 + 2| = | 2 | = 2
Image of 2 is f(2) = | 2 + 2| = | 4 | = 4
(b)
From (a),
f(–4) = 2
f(–3) = 1
f(0) = 2
f(2) = 4
Determine the point where the graph touches the x-axis.
At x-axis, f (x) = 0
|x + 2| = 0
x + 2 = 0
x = –2

Therefore, range of values of f (x) is 0 ≤ f (x) ≤ 4.
Notation of Function
As shown in figure above, for a function
, each element x in the domain X has a unique image y in the codomain Y.
The function can be written as:
- For , we say y is a function of x.
- f(x) is also called the value of the function f at x.
- f(x) is read as "f of x".
Example:
Given the function , find the value of
a.
b.
c.
Answer:
(a)
(b)
(c)
Given the function , find the value of
a.
b.
c.
Answer:
(a)
(b)
(c)
1.2 Function – An Introduction

- A function is a relation in which every element in the domain has a unique image (exactly one) in the codomain.
- One-to-one relation and many-to-one relation are examples of a special kind of relation which we call function.

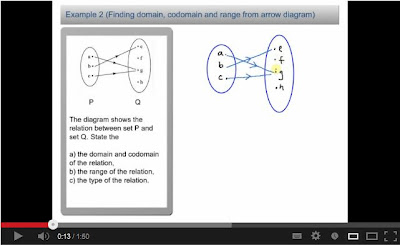
1.1.3 Types of Relation
- Relation can be classified into 4 types:
- One-to-one relation
- Many-to-one relation
- One-to-many relation
- Many-to-many relation
1.1b Domain and Codomain
[adinserter block="3"]
Domain and Codomain
- In the relation between one set and another, the first set is known as the domain and the second set is known as the codomain.
- Elements in the domain is called objects, whereas elements in the codomain mapped to the objects is called the image.
- Elements in the codomain not mapped to the objects are not the image.
- All images in codomain can be written as a set known as range.
Example:
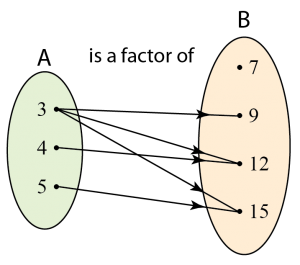
Domain = {3, 4, 5}
Codomain = {7, 9, 12, 15}
Range = {9, 12, 15} [Note: 7 is not an image because it is not mapped to any object.]
3 is the object of 9, 12 and 15.
4 is the object of 12.
5 is the object of 15.
9, 12 and 15 are the images of 3.
12 is the image of 4.
15 is the image of 5.

Domain = {3, 4, 5}
Codomain = {7, 9, 12, 15}
Range = {9, 12, 15} [Note: 7 is not an image because it is not mapped to any object.]
3 is the object of 9, 12 and 15.
4 is the object of 12.
5 is the object of 15.
9, 12 and 15 are the images of 3.
12 is the image of 4.
15 is the image of 5.
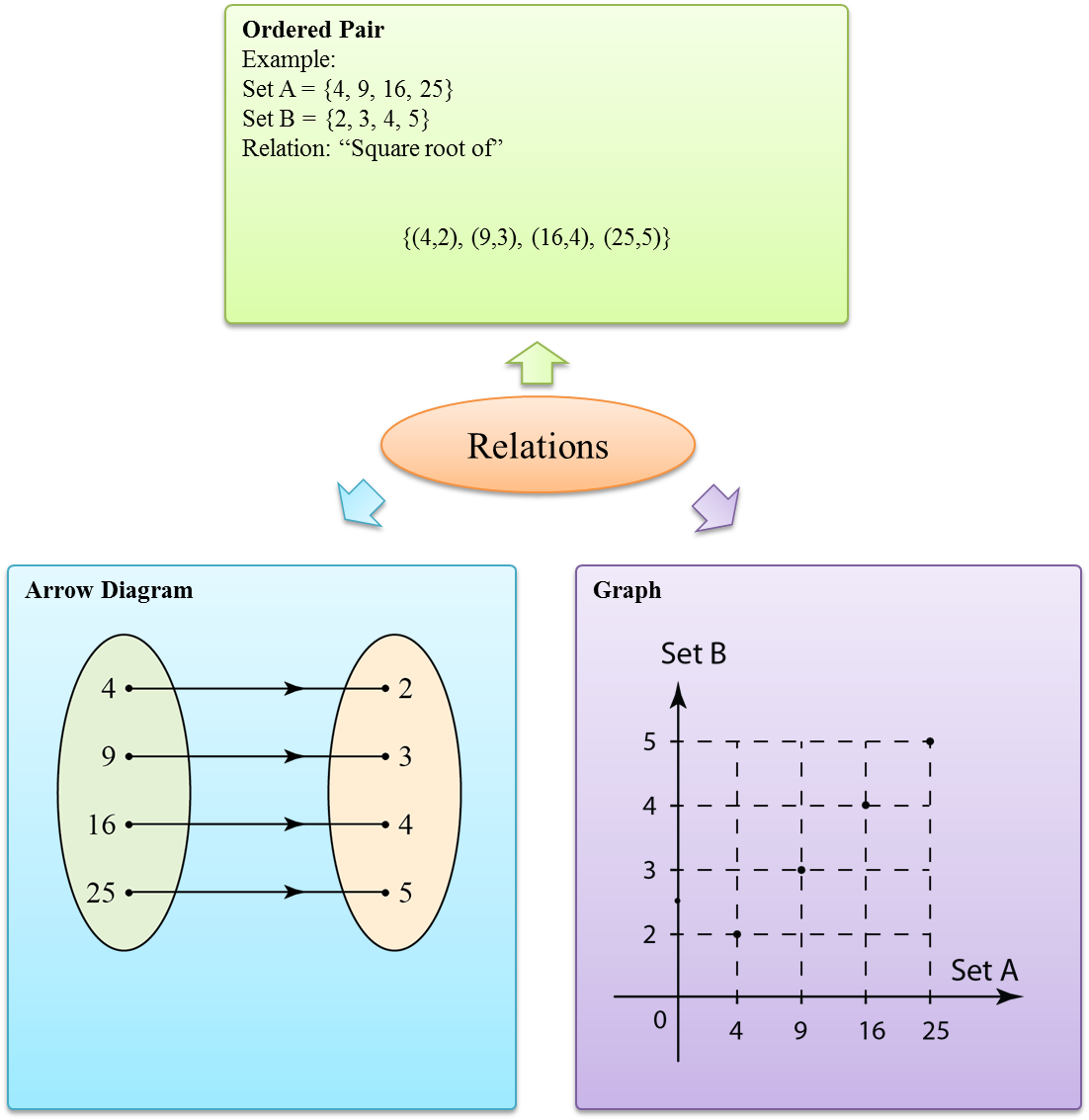
1.1a Relations
- A relation connects elements in set A (domain) to elements in set B (codomain) according to the definition of the relation.
- Relation can be represented in 3 forms:
- Ordered pair
- Arrow diagram
- Graph
10.6.5 Generation of Electricity from Nuclear Fission
Nuclear Reactor
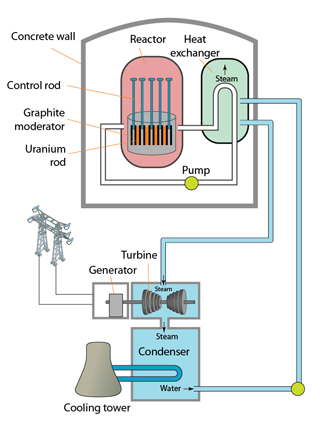
- A nuclear reactor produces tremendous amount of energy through nuclear fission.
- The energy liberated from the fusion of nuclear fuel heats the surrounding water.
- As a result, steam is generated to drive turbines, which in turn drive the electrical generators.
- The main components of a nuclear reactor:
- Graphite moderator
Fast moving neutrons are slowed down by collisions with nuclei in the moderator so that they can cause further fissions. In some nuclear power plant, the moderator is water. - Uranium rod (Fuel)
Fission reactions occur in the uranium rod to produce nuclear energy. The uranium used is often 'enriched' by increasing the proportion of the isotope uranium-235 above the natural value of 0.7% to 3%. - Control rod
The rate of the fission reaction is controlled by inserting or withdrawing these rods. The nuclei in the rods absorb neutrons without undergoing any reaction. Sometimes the rod is made of cadmium. - Coolant
To take away the heat from the nuclear reactor. Substances with high specific heat capacity such as 'heavy' water and carbon dioxide are used. - Thick concrete wall
To prevent the escape of harmful radiations. - Steam generator
Water in the generator is heated and changed into steam. The steam then drives the turbines. - Turbine
To turn the dynamo in the electrical generator to produce electricity.
- Graphite moderator
10.6.4 Nuclear Fusion
- In nuclear fusion, two or more small and light nuclei come together to form a heavier nucleus.
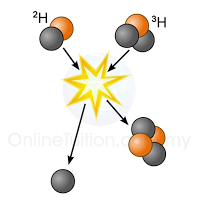
- This process is accompanied by the release of a huge amount of energy.
- Below are two examples of fusion reactions:
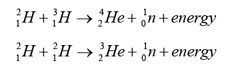
- Fusion is much more difficult to achieve than fission because the hydrogen nuclei repel each other. Therefore, the nuclei must be heated to 108 K or more so that the nuclei will have enough of kinetic energy to overcome the electrical repulsion between the nuclei.
- Example
- The Sun get its energy from the fusion of hydrogen nuclei.
- A hydrogen bomb uses the principle of nuclear fusion for its design.
10.6.3 Chain Reaction
- If neutrons from the fission of uranium-235 continue to split other nuclei causing further fission, a chain reaction has occurred.
- The number of nuclei which undergo fission multiplies rapidly.
- In order for a chain reaction to take place, a minimum of one neutron from each fission must trigger further fission.
- At the same time, the mass of fission material must exceed a certain minimal mass known as the critical mass. If the material is less than this value, too many neutrons escape without hitting nuclei, preventing a chain reaction from happening.
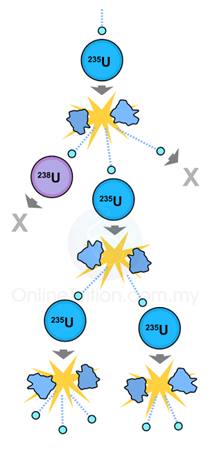 |
| (Chain Reaction) |