7.2 Kebarangkalian Gabungan Dua Peristiwa
1. Untuk dua peristiwa, A dan B, dalam ruang sampel S, peristiwa A ∩ B (A dan B) dan A υ B(A atau B) dikenali sebagai peristiwa bergabung.
2. Kebarangkalian suatu peristiwa A atau peristiwa B berlaku (Kesatuan set A dan set B), boleh ditentukan dengan rumus yang berikut:
3. Kebarangkalian kesatuanset A dan set B juga boleh ditentukan dengan rumus alternatif yang berikut:
4. Kebarangkalian suatu peristiwa A dan suatu peristiwa B berlaku P(A ∩ B) (Persilangan set A dan set B), boleh ditentukan dengan rumus yang
berikut:
Contoh:
Diberi set semesta ialah ξ = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. Satu nombor dipilih secara rawak daripada set ξ. Cari kebarangkalian bahawa
(a) suatu nombor genap terpilih,
(b) suatu nombor ganjil atau nombor perdana terpilih.
Penyelesaian:
Ruang sampel, S, ialah ξ
n(S) = 14
(a)
Katakan A = Peristiwa suatu nombor genap dipilih
A = {2, 4, 6, 8, 10, 12, 14}
n(A) = 7
(b)
B = Peristiwa nombor yang dipilih itu ialah nombor ganjil
C = Peristiwa nombor yang dipilih itu ialah nombor perdana
B = {3, 5, 7, 9, 11, 13, 15} dan n(B) = 7
C = {2, 3, 5, 7, 11, 13} dan n(C) = 6
Peristiwa nombor yang dipilih itu ialah ‘nombor ganjil atau nombor perdana’ ialah B υ C.
P(B υ C) = P(B) + P(C) – P(B ∩ C)
B ∩ C = {3, 5, 7, 11, 13}, n(B ∩ C) = 5
Maka, kebarangkalian bahawa nombor yang dipilih itu ialah nombor ganjil atau nombor perdana ialah =
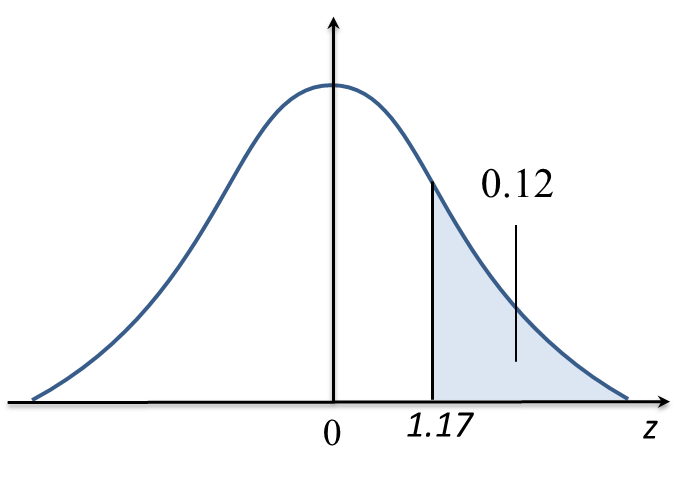 Oleh itu, markah minimum untuk mendapat gred A ialah 66.
Oleh itu, markah minimum untuk mendapat gred A ialah 66.