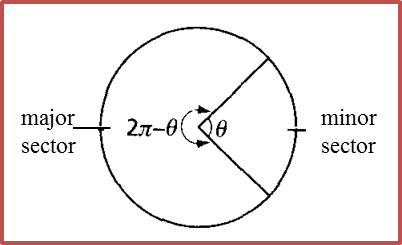
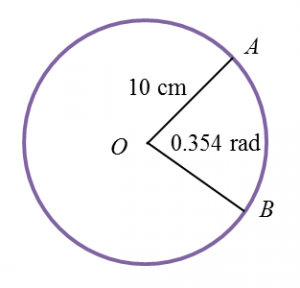
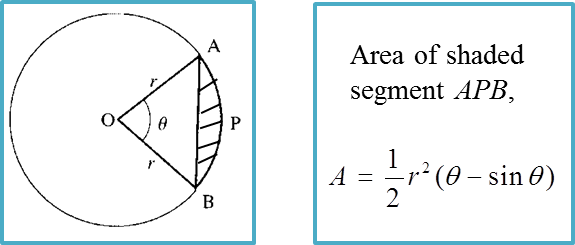
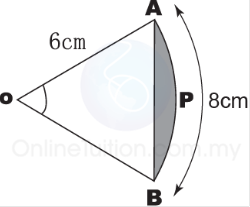
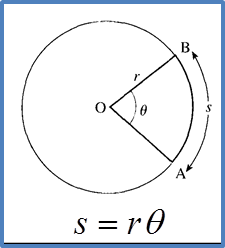
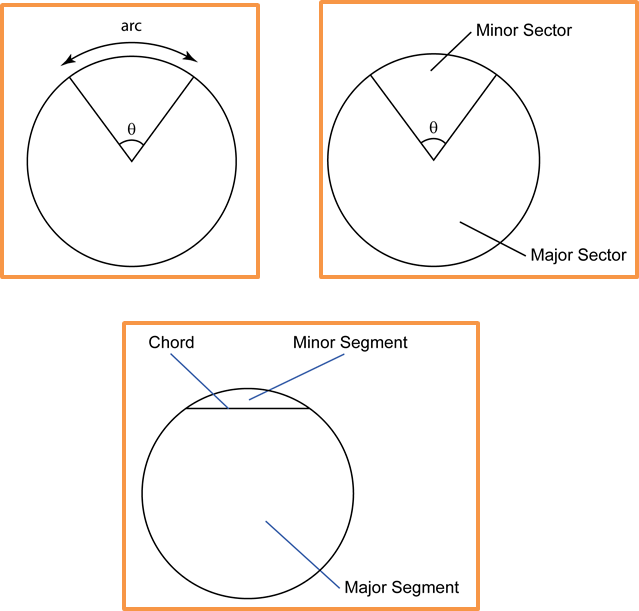
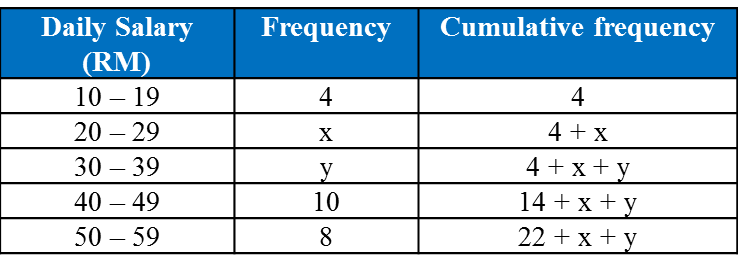
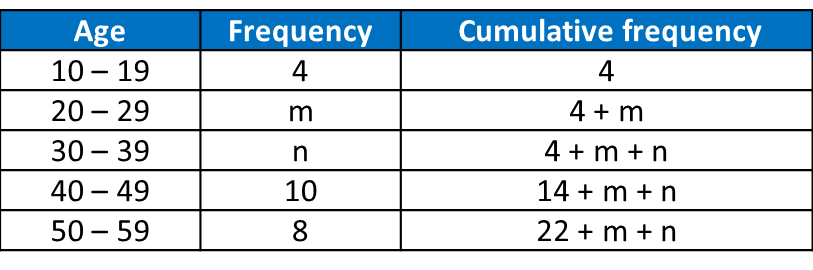
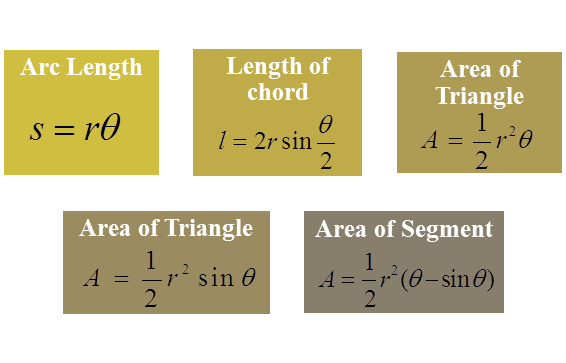Question 1:
(a)
(b)

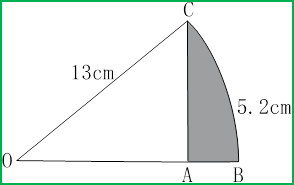
The figure shows the sector OCB of radius 13 cm at the centre O. The length of the arc CB = 5.2 cm. Find
(a) the angle in radians,
(b) the perimeter of the shaded region.
Solution:(a)
(b)
Perimeter of the shaded region = 5.07 + 1.03 + 5.2 = 11.3 cm.
Question 2:
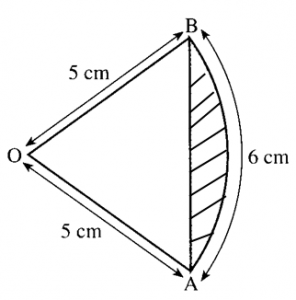
The figure shows the sector AOB of a circle, centre O and radius 5 cm. The length of the arc AB is 6 cm. Find the area of:
Solution:
(a) Arc AB = 6cm

The figure shows the sector AOB of a circle, centre O and radius 5 cm. The length of the arc AB is 6 cm. Find the area of:
(a) the sector AOB,
(b) the shaded region.
Solution:
(a) Arc AB = 6cm
s = r θ
6 = 5 θ
θ = 6/5 rad
(b)