5.7 SPM Practice (Long Questions 4)

Question 7:


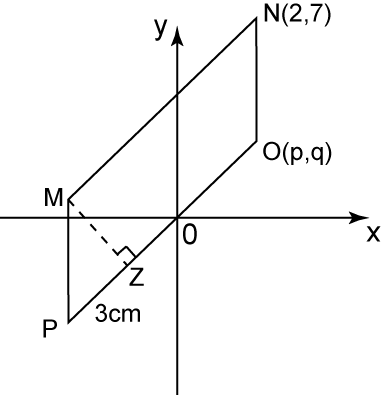
The diagram above shows a parallelogram on a Cartesian plane. MP and NO are parallel to the y-axis. Given that the distance of MZ is 4 units. Find
(a) the value of p and q.
(b) the equation of the straight line MN.

Solution:
$\begin{array}{l}\text{(a)}\\ \text{Line }NO\text{ is parallel to }y\text{-axis,}\\ p=2\\ \\ MP=\sqrt{3^2+4^2}\\ =\sqrt{9+16}\\ =\sqrt{25}\\ =5\\ NO=MP=5\text{ units}\\ q=7-5=2\end{array}$


$\begin{array}{l}\text{(b)}\\ \text{Point }O=\left(2,2\right)\\ \text{Gradient }PO=\frac{2-0}{2-0}=1\\ \\ \text{Gradient }MN=g\text{radient }PO=1\\ y_1=m{x}_1+c\\ 7=1\left(2\right)+c\\ c=5\\ \\ \text{Equation of line }MN\text{ is}\\ y=x+5\end{array}$

Question 8:


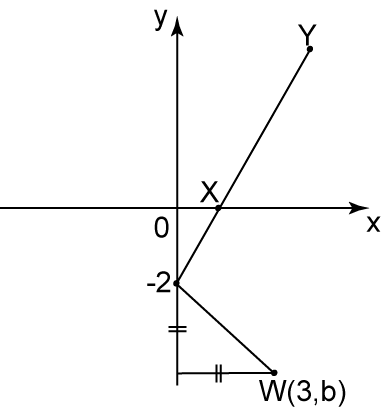
The diagram above shows that two straight line intersect at point (0 , -2). Find
(a) the value of b
(b) the x-intercept of the straight line XY if the gradient of XY is equal to 2.
(c) the equation of XY.

Solution:
(a)
Value of b
= 2 units + 3 units
= 5 units
= –5

$\begin{array}{l}(b)\\ \text{Given }m=2,c=-2\\ \text{For }x\text{-intercept, }y=0\\ 0=2x+\left(-2\right)\\ 0=2x-2\\ 2x=2\\ x=1\\ \text{Therefore }x\text{ intercept of }XY=1.\end{array}$

$\begin{array}{l}\text{(c)}\\ \text{Substitute }m=2\text{ and }(0,-2)\text{ into }y=mx+c\\ y=2x+\left(-2\right)\\ y=2x-2\\ \text{Therefore equation of }XY:y=2x-2\end{array}$