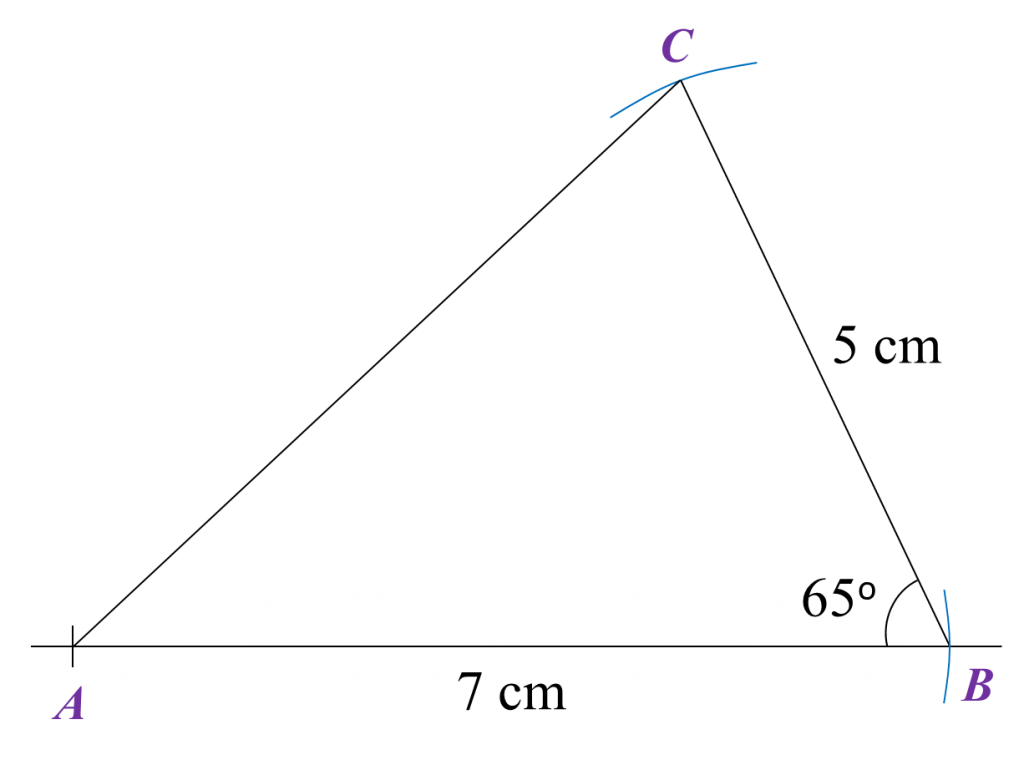
Question 6:
Diagram below in the answer space shows part of a triangle ABC.
Answer:
(a)

Solution:
(a)
(b)
Diagram below in the answer space shows part of a triangle ABC.
Answer:
(a)

Solution:
(a)

(b)
Question 7:
Diagram below shows a quadrilateral ABQR.
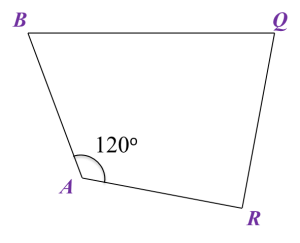
(a) Using only a ruler and a pair of compasses, construct the diagram using the measurement given.
Begin from the straight lines AB and BQ provided in the answer space.
(b) Based on the diagram constructed in (a), measure the length, in cm, of QR.
Answer:
(a)

Solution:
(a)

(b)
QR = 5.9 cm
Diagram below shows a quadrilateral ABQR.
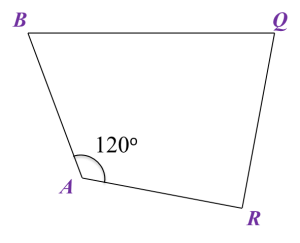
(a) Using only a ruler and a pair of compasses, construct the diagram using the measurement given.
Begin from the straight lines AB and BQ provided in the answer space.
(b) Based on the diagram constructed in (a), measure the length, in cm, of QR.
Answer:
(a)

Solution:
(a)

(b)
QR = 5.9 cm



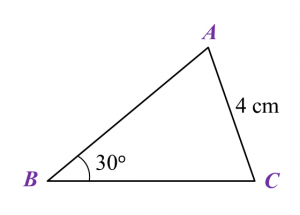
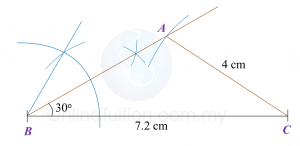




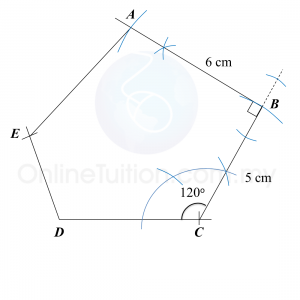


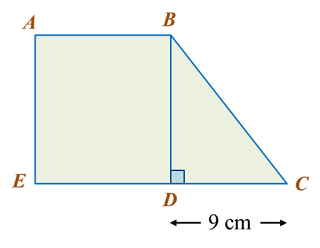
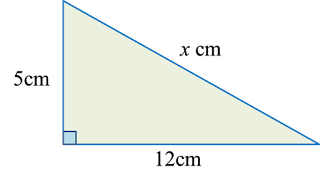
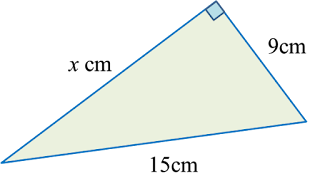
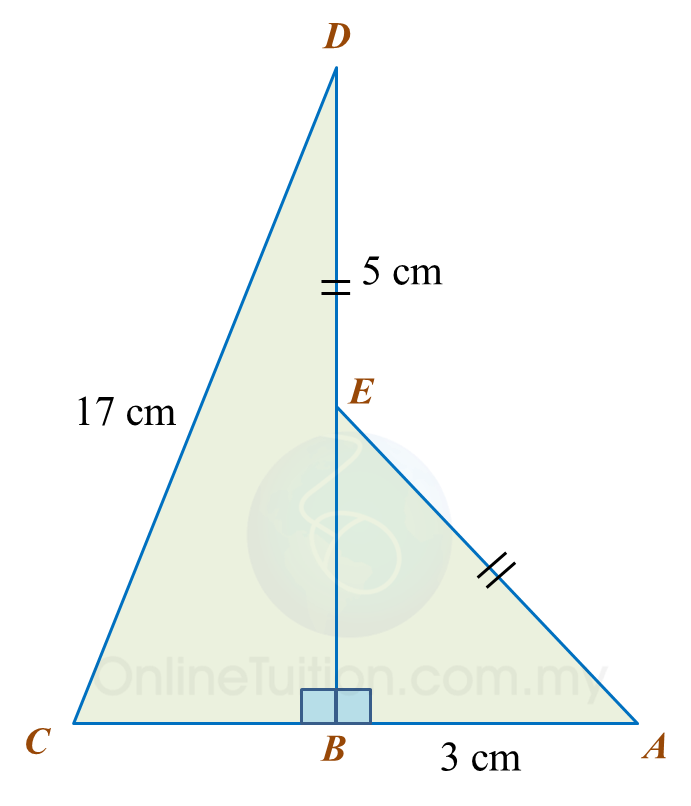 Find the length, in cm, of BC. Round off the answer to two decimal places.
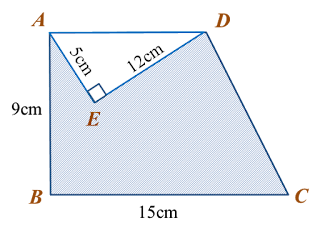
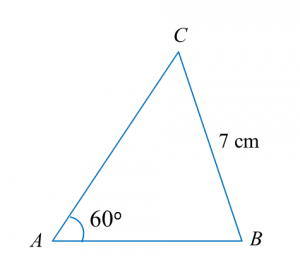
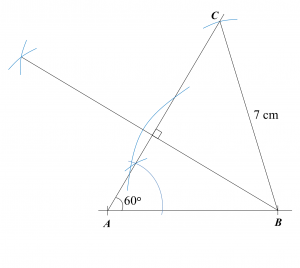
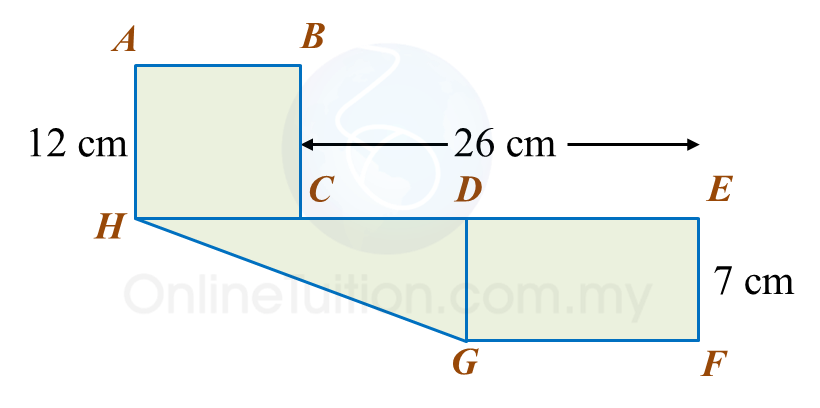
Find the length, in cm, of BC. Round off the answer to two decimal places.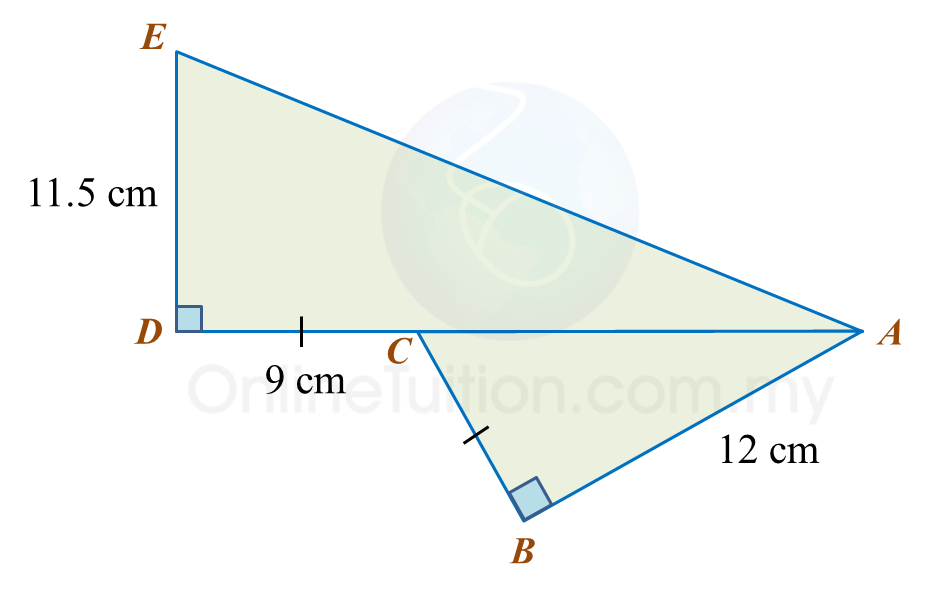 Find the length, in cm, of AE. Round off the answer to one decimal places.
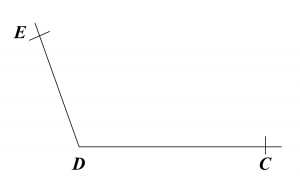
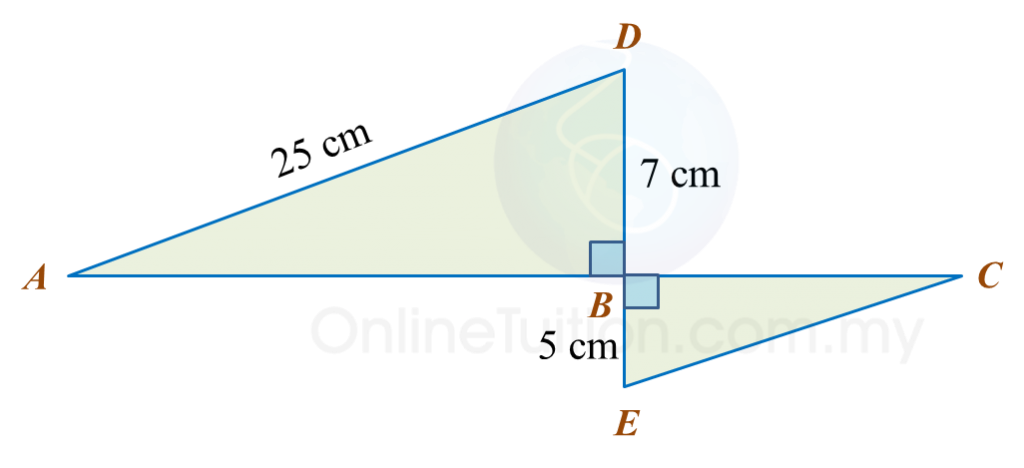
Find the length, in cm, of AE. Round off the answer to one decimal places.