Question 7:
Diagram below in the answer space shows a circle with centre O drawn on a grid of equal squares with sides of 1 unit. POQ is a diameter of the circle.
W, X and Y are three moving points inside the circle.
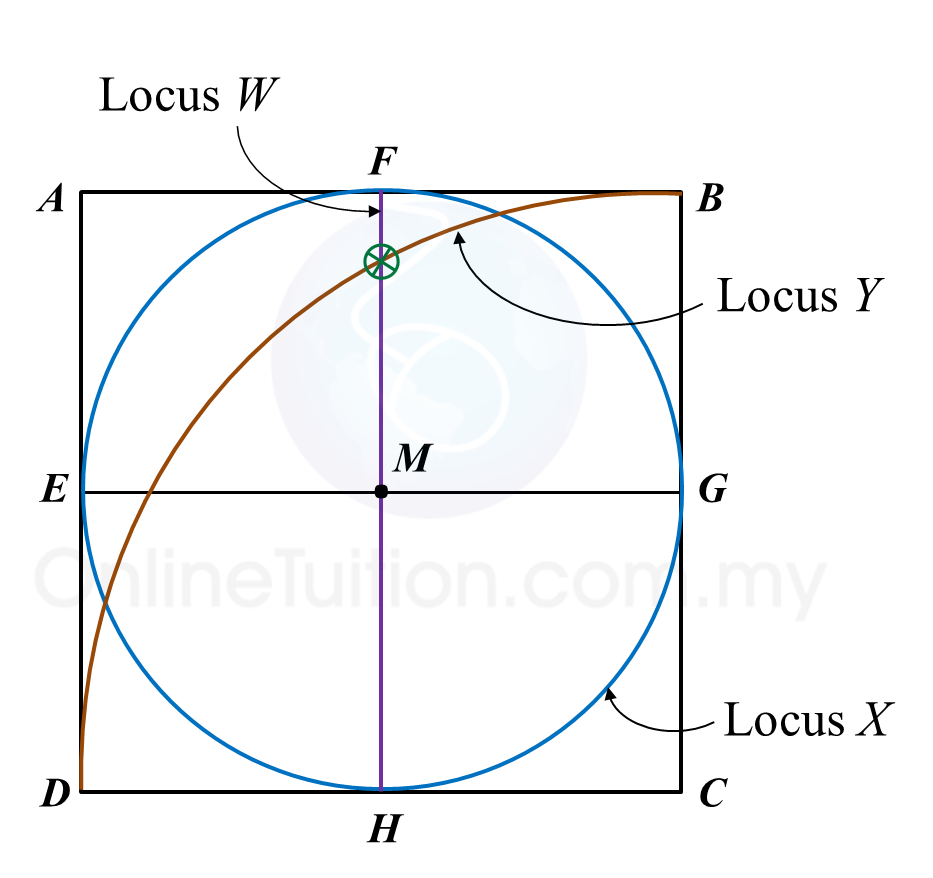
(a) W is the point which moves such that it is constantly 4 units from the point O. Describe fully the locus of W.
(b) On the diagram, draw,
(i) the locus of the point X which moves such that its distance is constantly 3 units from the line PQ,
(ii) the locus of the point Y which moves such that it is equidistant from the point P and the point Q.
(c) Hence, mark with the symbol the intersection of the locus of X and the locus of Y.
Answer:
(b)(i),(ii) and (c)
Solution:
(a) The locus of W is a circle with the centre O and a radius of 4 units.
(b)(i),(ii) and (c)
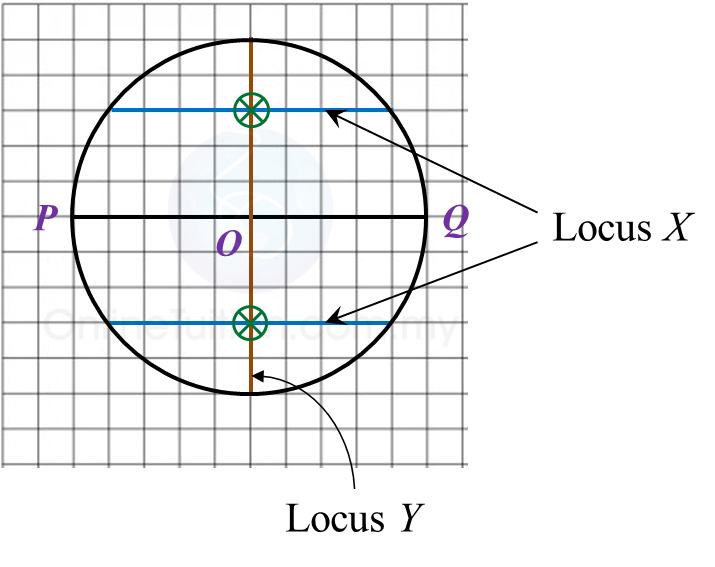
Diagram below in the answer space shows a circle with centre O drawn on a grid of equal squares with sides of 1 unit. POQ is a diameter of the circle.
W, X and Y are three moving points inside the circle.
(a) W is the point which moves such that it is constantly 4 units from the point O. Describe fully the locus of W.
(b) On the diagram, draw,
(i) the locus of the point X which moves such that its distance is constantly 3 units from the line PQ,
(ii) the locus of the point Y which moves such that it is equidistant from the point P and the point Q.
(c) Hence, mark with the symbol the intersection of the locus of X and the locus of Y.
Answer:
(b)(i),(ii) and (c)

Solution:
(a) The locus of W is a circle with the centre O and a radius of 4 units.
(b)(i),(ii) and (c)

Question 8:
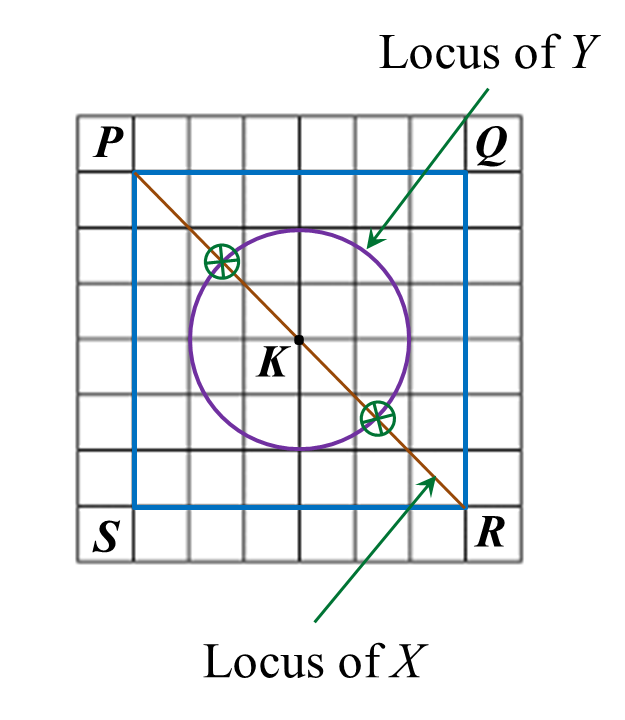
The diagram in the answer space shows two squares ABCD and CDEF each of sides 4 cm. K is a point on the line CD. W, X and Y are three moving points in the diagram.
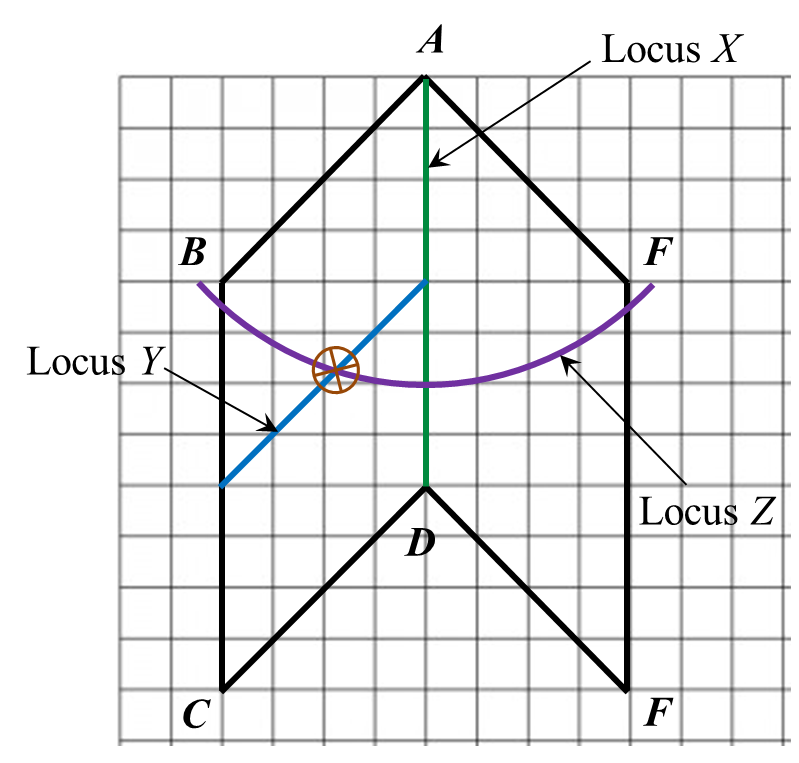
(a) Point W moves such that it is always equidistant from the straight lines AB and EF. By using the letters in diagram, state the locus of W.
(b) On the diagram, draw
(i) the locus X such that it is always 2 cm from the straight line ACE,
(ii) the locus of Y such that KY = KC.
(c) Hence, mark with the symbol the intersection of the locus of X and the locus of Y.
Answer:
(b)(i), (ii) and (c)
Solution:
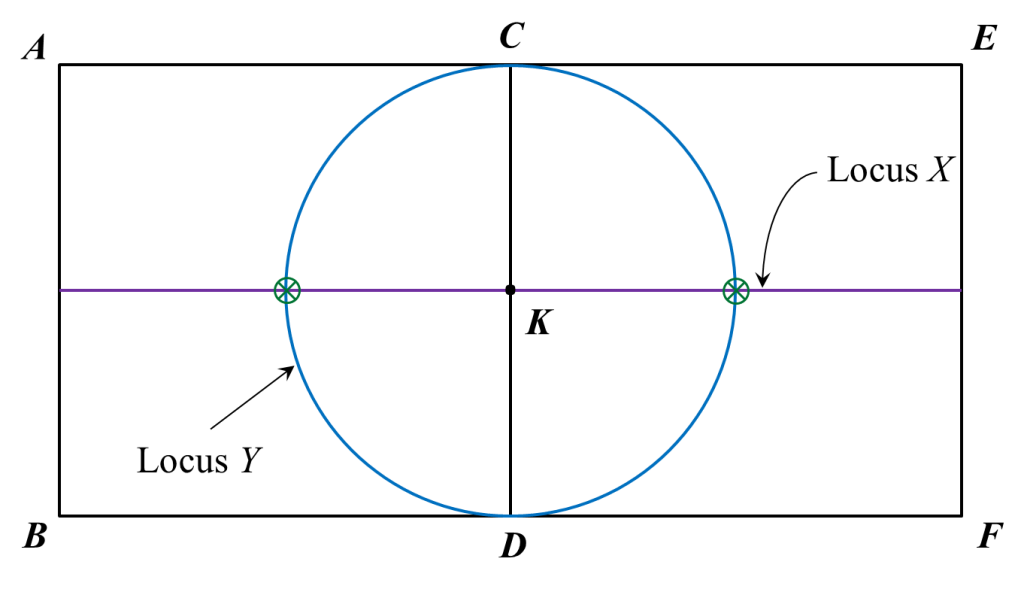
(a) The locus of W is the line CD.
(b)(i),(ii) and (c)
The diagram in the answer space shows two squares ABCD and CDEF each of sides 4 cm. K is a point on the line CD. W, X and Y are three moving points in the diagram.
(a) Point W moves such that it is always equidistant from the straight lines AB and EF. By using the letters in diagram, state the locus of W.
(b) On the diagram, draw
(i) the locus X such that it is always 2 cm from the straight line ACE,
(ii) the locus of Y such that KY = KC.
(c) Hence, mark with the symbol the intersection of the locus of X and the locus of Y.
Answer:
(b)(i), (ii) and (c)

Solution:
(a) The locus of W is the line CD.
(b)(i),(ii) and (c)

Question 9:
Diagram below shows a Cartesian plane.
Draw the locus of X, Y and Z.
(a) X is a point which moves such that its distance is constantly 4 units from the origin.
(b) Y is a point which moves such that it is always equidistant from point K and point L.
(c) Z is a point which moves such that it is always equidistant from lines KM and y-axis.
Answer:
Solution:
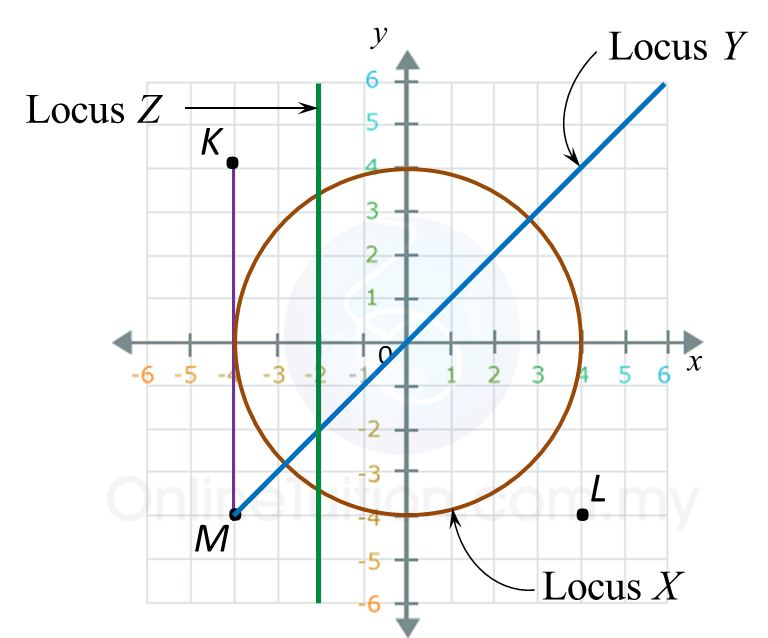
Diagram below shows a Cartesian plane.
Draw the locus of X, Y and Z.
(a) X is a point which moves such that its distance is constantly 4 units from the origin.
(b) Y is a point which moves such that it is always equidistant from point K and point L.
(c) Z is a point which moves such that it is always equidistant from lines KM and y-axis.
Answer:

Solution:

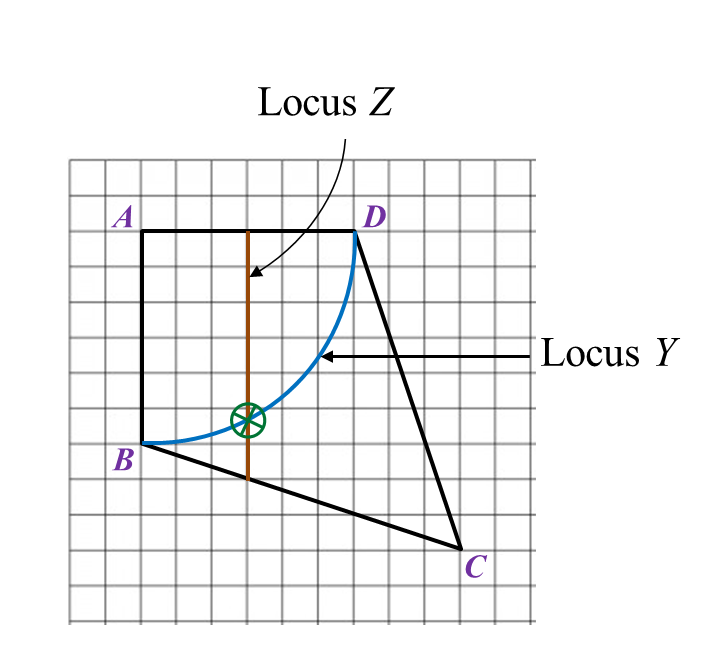

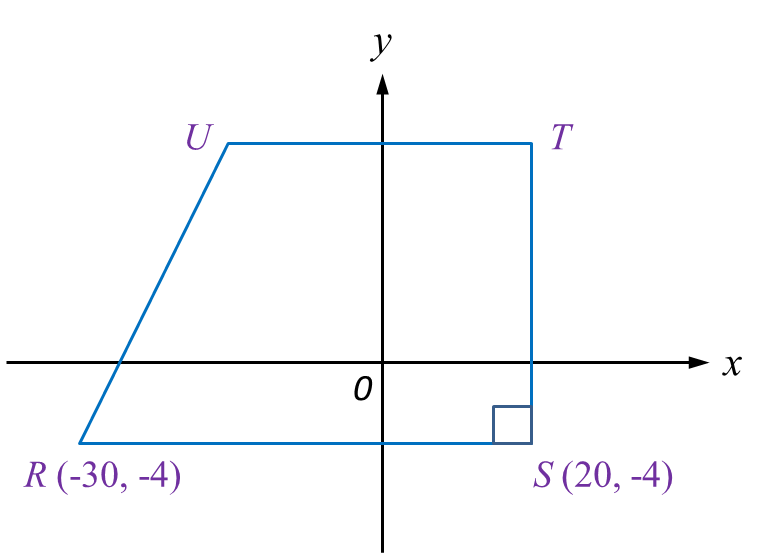
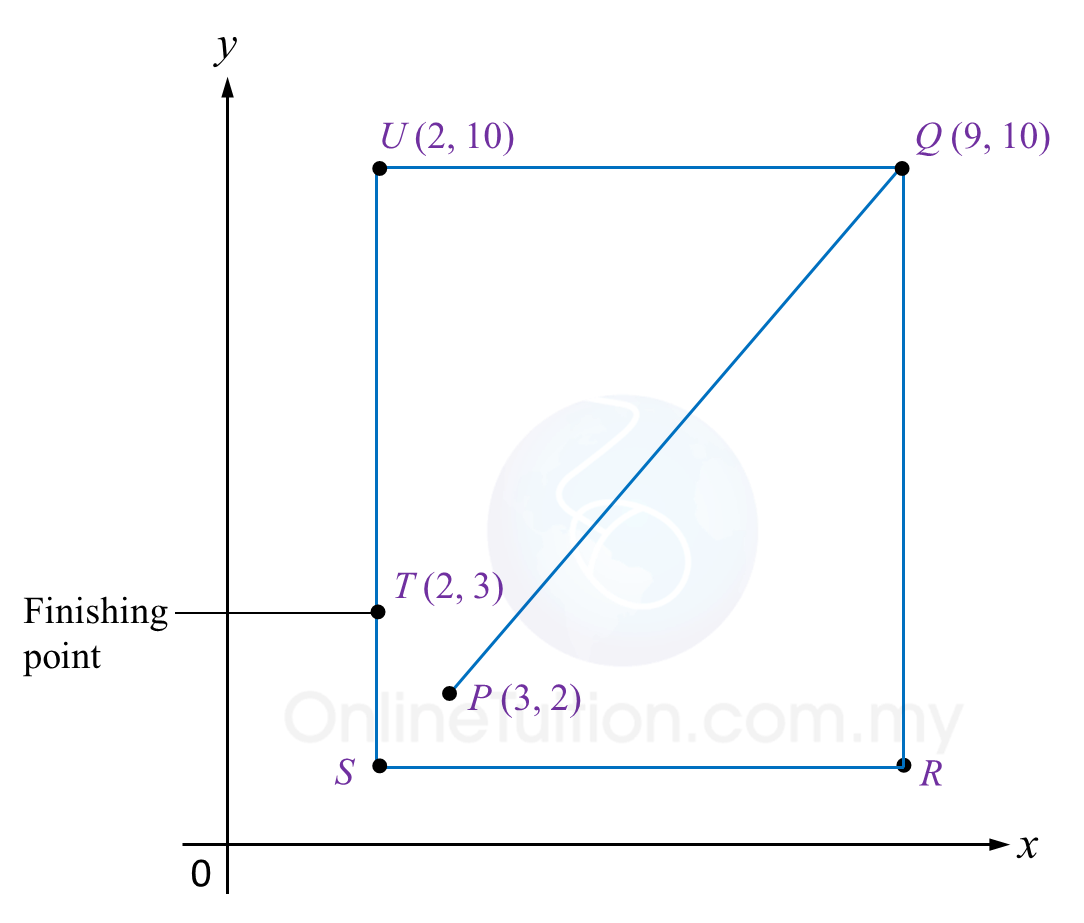 The route of male participants is PQUT while the route for female participants is QRST. QR is parallel to UT whereas UQ is parallel to SR.
The route of male participants is PQUT while the route for female participants is QRST. QR is parallel to UT whereas UQ is parallel to SR.