Question 6:
In Diagram below, PQRST is a straight line. Find the value of x.
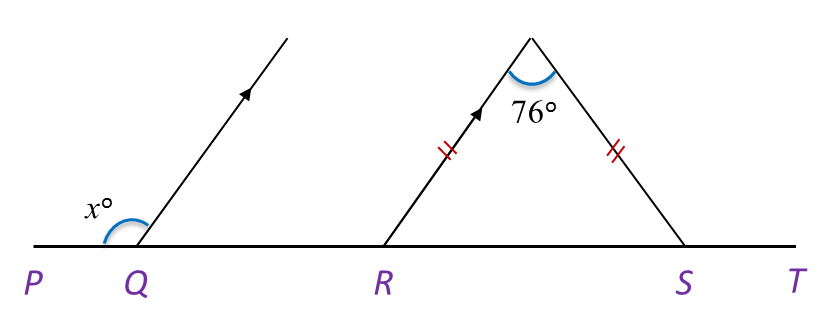
Solution:
In Diagram below, PQRST is a straight line. Find the value of x.

Solution:
Question 7:
In Diagram below, find the value of y.

Solution:
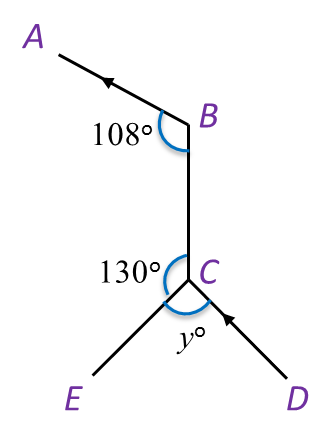
In Diagram below, find the value of y.

Solution:

Question 8:
In Diagram below, PSR and QST are straight lines.
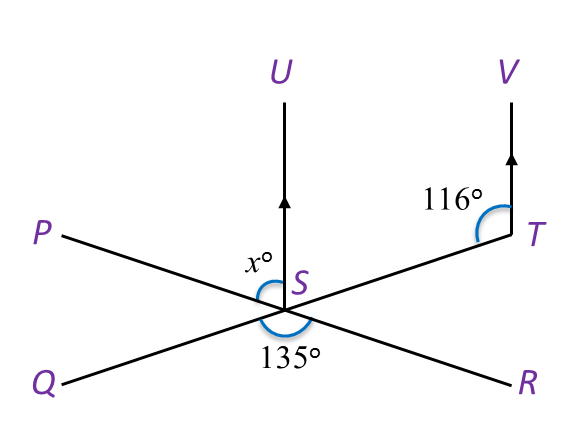 Find the value of x.
Find the value of x.
Solution:
In Diagram below, PSR and QST are straight lines.
 Find the value of x.
Find the value of x.Solution:
Question 9:
In Diagram below, PWV is a straight line.
 (a) Which line is perpendicular to line PWV?
(a) Which line is perpendicular to line PWV?
(b) State the value of ∠ RWU.
Solution:
(a) SW
(b) ∠ RWU = 13o + 29o + 20o = 62o
In Diagram below, PWV is a straight line.
 (a) Which line is perpendicular to line PWV?
(a) Which line is perpendicular to line PWV?(b) State the value of ∠ RWU.
Solution:
(a) SW
(b) ∠ RWU = 13o + 29o + 20o = 62o
Question 10:
In Diagram below, UVW is a straight line.

(a) Which line is parallel to line TU?
(b) State the value of ∠ QVS.
Solution:
(a) QV
(b) ∠ QVS = 8o + 18o = 26o
In Diagram below, UVW is a straight line.

(a) Which line is parallel to line TU?
(b) State the value of ∠ QVS.
Solution:
(a) QV
(b) ∠ QVS = 8o + 18o = 26o


 h2 = 32 + 42
h2 = 32 + 42 
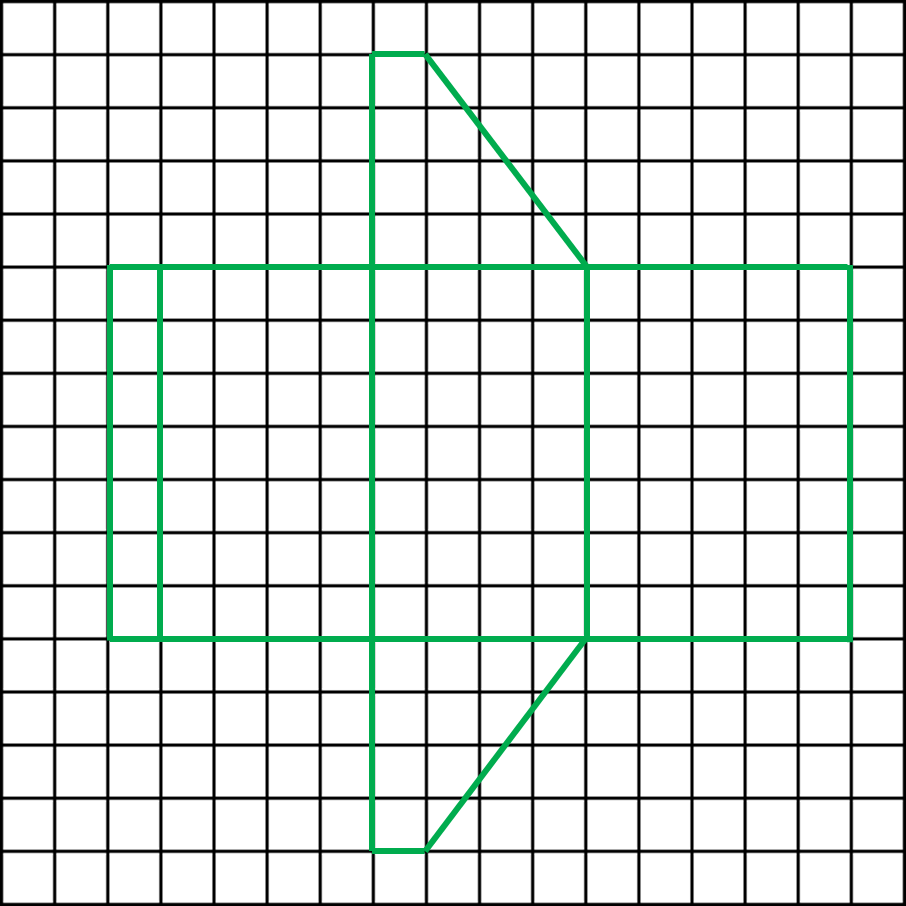
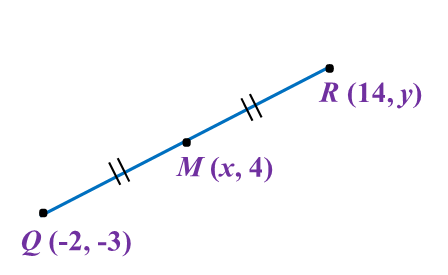 The value of x and y are
The value of x and y are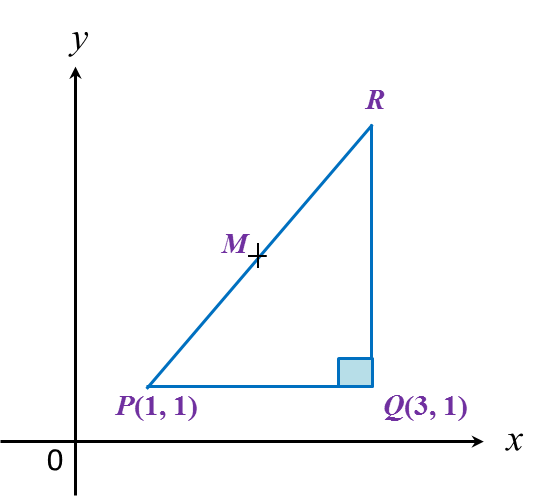
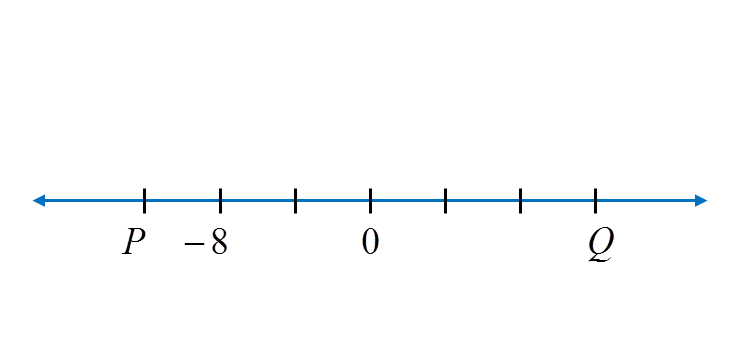 What is the value of P and of Q?
What is the value of P and of Q?