Home › 2017 › December

Monthly Archives: December 2017

2.2.2 Polygons II, PT3 Practice

Posted on by

Question 6:
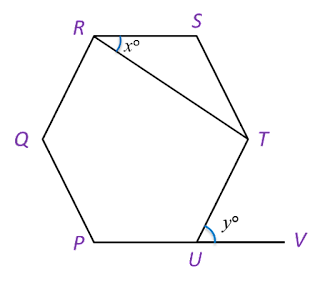
In diagram below, PQRSTU is a regular hexagon QUV is a straight line.



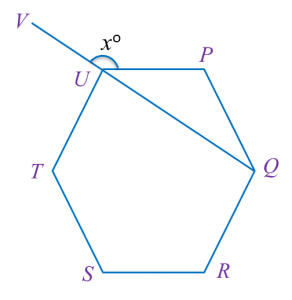
Find the value of x.

Solution:
Each interior angle = ( 6−2 )× 180 o 6 = 120 o ∠PUQ= 180 o − 120 o 2 = 30 o  (△PUQ is a isosceles triangle) x o = 180 o − 30 o = 150 o x=150



Question 7:
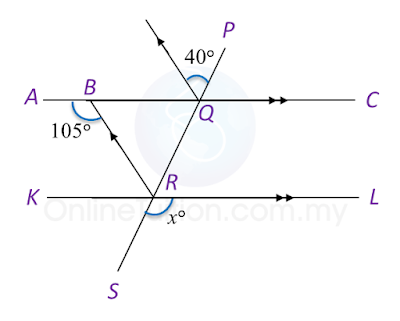
In diagram below, PQRSTU is a hexagon. UPE, PQF, QRG, RSH and UTJ are straight lines.



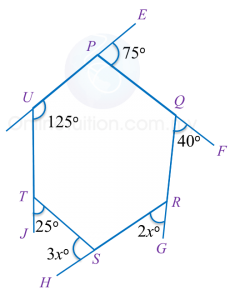
Find the value of x.

Solution:
Sum of all the exterior angles of any polygon= 360 o 25 o +3 x o +2 x o + 40 o + 75 o + 55 o = 360 o 5 x o + 195 o = 360 o   5 x o = 360 o − 195 o    = 165 o x o = 165 o ÷5    = 33 o  x=33



Question 8:
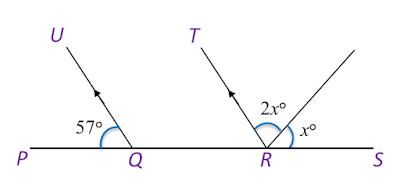
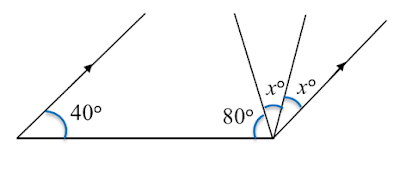
In Diagram below, A, B, C, D and E are vertices of a 9 sided regular polygon.

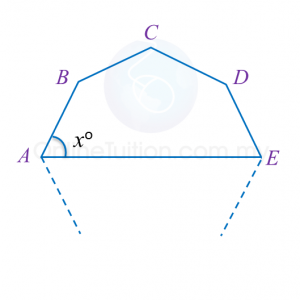
Find the value of x.

Solution:
Exterior angle = 360 o 9 = 40 o Interior angle= 180 o − 40 o = 140 o Sum of interior angles of pentagon ABCDE =( 5−2 )× 180 o = 540 o x o + 140 o + 140 o + 140 o + x o = 540 o 2 x o = 540 o − 420 o  = 120 o    x o = 60 o    x=60


2.2.1 Polygons II, PT3 Practice

Posted on by

2.2.1 Polygons II, PT3 Practice

Question 1:
Diagram below shows a pentagon PQRST. TPU and RSV are straight lines.
Find the value of x.

Solution:
Sum of interior angles of a pentagon =( 5−2 )× 180 o =3× 180 o = 540 o ∠TSR= 180 o − 70 o           = 110 o ∠TPQ= 180 o − 85 o           = 95 o x o = 540 o −( 110 o + 105 o + 115 o + 95 o )     = 540 o − 425 o     = 115 o    x=115


Question 2:
In Diagram below, PQRSTU is a hexagon. APQ and BTS are straight lines.
Find the value of x + y.

Solution:
∠ Q P U = 180 o − 160 o = 20 o Reflex ∠ P U T = 360 o − 80 o = 280 o ∠ U T S = 180 o − 120 o = 60 o ∠ T S R = 180 o − 35 o = 145 o Sum of interior angles of a hexagon = ( 6 − 2 ) × 180 o = 720 o x o + y o + 145 o + 60 o + 280 o + 20 o = 720 o x o + y o = 720 o − 505 o = 215 o x + y = 215


Question 3:
Diagram below shows a regular hexagon PQRSTU. PUV is a straight line.
Find the value of x + y.

Solution:
Size of each interior angle of a regular hexagon = ( 6 − 2 ) × 180 o 6 = 120 o x o = 180 o − 120 o 2 = 30 o y o = 180 o − 120 o = 60 o x o + y o = 30 o + 60 o = 90 o x + y = 90


Question 4:
In the diagram below, KLMNP is a regular pentagon. LKS and MNQ are straight lines.
Find the value of x + y.
 
Solution:
Size of each interior angle of a regular pentagon = ( 5 − 2 ) × 180 o 5 = 108 o ∠ P K S = ∠ P N Q = 180 o − 108 o = 72 o Reflex angle ∠ K P N = 360 o − 108 o = 252 o

Sum of interior angles of a hexagon = ( 6 − 2 ) × 180 o = 720 o ∴ x o + y o + 72 o + 252 o + 72 o + 100 o = 720 o x o + y o = 720 o − 496 o = 224 o x + y = 224


Question 5:
In Diagram below, PQR is an isosceles triangle and PRU is a straight line.
Find the value of x + y.

Solution:
x o = 180 o − 20 o − 20 o = 140 o ∠ P R S = 180 o − 110 o = 70 o y o + 85 o + 75 o + 70 o = 360 o y o + 230 o = 360 o y o = 130 o x o + y o = 140 o + 130 o = 270 o x + y = 270
 

2.1 Polygons II

Posted on by

2.1 Polygons II
 
2.1.1 Regular Polygons
1.  A regular polygon is a polygon where
(a) all its sides are of equal length, and
(b) all its interior angles are of equal size.

2. The number of axis of symmetry of a regular polygon is equal to its number of sides.

Example:


2.1.2 Exterior and Interior Angles of Polygons
1. The exterior and interior angles at a vertex of a polygon is supplementary.

2. The sum of interior angles of an n-sided polygon is  ( n − 2 ) × 180 o  

3. Each interior angle of a regular n-sided polygon is ( n − 2 ) × 180 o n

4. The sum of all exterior angles of a polygon is 360o.

5. Each exterior angle of a regular n-sided polygon is  360 o n

SPM Form 4/Form 5 Biology Revision Notes

Posted on by

Form 4 Biology


 02 Cell Structure

Objective Questions

  1. Cell Structure and Function 1 (6 Questions) 
  2. Cell Structure and Function 2 (5 Questions) 
  3. Cell Organisation 1 (5 Questions) 
  4. Cell Organisation 2 (5 Questions) 
  5. Cell Organisation 3 (3 Questions) 


03 Movement across Plasma Membrane

Objective Questions

  1. Movement of Substances Across the Plasma Membrane 1 (5 Questions) 
  2. Movement of Substances Across the Plasma Membrane 2 (5 Questions) 
  3. Movement of Substances Across the Plasma Membrane 3 (5 Questions) 
  4. Movement of Substances Across the Plasma Membrane in Everyday Life (5 Questions) 


04 Chemical Composition of Cell Chemical

Objective Questions

  1. Composition of the Cell (3 Questions) 
  2. Carbohydrate (6 Questions) 
  3. Proteins (5 Questions) 
  4. Lipids (3 Questions) 
  5. Enzymes 1 (4 Questions) 
  6. Enzymes 2 (4 Questions) 


    05 Meiosis and Mitosis

    1. Mitosis
    2. Meiosis
    3. Appreciating the Movement of Chromosomes During Mitosis and Meiosis

    Objective Questions

    1. Mitosis 1 (6 Questions) 
    2. Mitosis 2 – (6 Questions) 
    3. Meiosis 1 – (6 Questions) 
    4. Meiosis 2 – (7 Questions) 


    06 Nutrition

    1. The Types of Nutrition
    2. The Concept of a Balanced Diet
    3. Malnutrition
    4. Food Digestion
      1. Digestion in the Mouth and Stomach
      2. Digestion in the Small Intestine
    5. The Process of Absorption and Assimilation of Digested Food
      1. Functions of the Liver and Assimilation
    6. The Formation of Faeces and Defecation
    7. Evaluating Eating Habits
    8. The Importance of a Healthy Digestive System
    9. The Importance of Macronutrients and Micronutrients in Plants
    10. Photosynthesis
    11. The Mechanism of Photosynthesis
    12. Factors Affecting Photosynthesis
    13. Practising a Caring Attitude Towards Plants
    14. The Technology Used in Food Production
    15. Technological Development in Food Processing

    Objective Questions

    1. Balanced Diet (6 Questions) 
    2. Malnutrition (3 Questions) 
    3. Food Digestion (7 Questions) 
    4. Absorption and Assimilation of Digested Food (4 Questions) 


    07 Respiration

    1. The Respiratory Process in Energy Production
    2. The Respiratory Structures and Breathing Mechanisms in Humans and Animals
    3. The Concept of Gaseous Exchange Across the Respiratory Surfaces and the Transport of Gases in Human
    4. The Regulatory Mechanism in Respiration
    5. The Importance of Maintaining a Healthy Respiratory System
    6. Respiration in Plants

    Objective Questions

    1. The Respiratory Process in Energy Production (4 Questions) 
    2. Respiratory Mechanisms in Humans and Animals (7 Questions) 
    3. Gaseous Exchange in Humans (4 Questions) 
    4. The Regulatory Mechanism in Respiration (4 Questions) 
    5. Respiration in Plants (4 Questions) 


    08 Dynamic Ecosystem

    1. The Abiotic and Biotic Components of The Environment
    2. The Processes of Colonisation and Succession in An Ecosystem
    3. Population Ecology
    4. The Concept of Biodiversity
    5. The Impact of Microorganisms on Life
    6. Appreciating Biodiversity

    Objective Questions

    1. The Abiotic and Biotic Components of the Environment (7 Questions) 
    2. The Process of Colonisation and Sucession in an Ecosystem (3 Questions) 
    3. Population Ecology (3 Questions) 
    4. Biodiversity (3 Questions) 
    5. The Impact of Microorganisms on Life (6 Questions) 


    09 Endangered Ecosystem

    1. Human Activities that Endanger the Ecosystem
    2. The Greenhouse Effect and Thinning of the Ozone Layer
    3. The Importance of Proper Management of Development Activities and the Ecosystem

    Objective Questions

    1. Human Activities that Endanger the Ecosystem (7 Questions) 
    2. The Greenhouse Effect and Thinning of the Ozone Layer (6 Questions) 
    3. Proper Management of Development Activities and the Ecosystem (3 Questions)



    Form 5 Biology

    01 Transport

    1. The Importance of Transport System in Multicellular Organisms
    2. The Concept of Circulatory System
      1. Composition of Human Blood
      2. Function of Blood in Transport
      3. Function of Haemolymph in Transport
      4. Types of Circulatory System
      5. Circulatory System in Humans
        1. The Blood Vessels
        2. The Heart
        3. Circulation of Blood in Humans
      6. Regulation of Blood Pressure
    3. Blood Clotting
      1. Mechanism of Blood Clotting
      2. Consequences of Blood Clotting Related Problem
    4. The Lymphatic System
      1. Formation of the Interstitial Fluid and Lymph
      2. Structure of the Lymphatic System
      3. Relationship between the Composition of Blood, Interstitial Fluid and Lymph
      4. Relationship between the Lymphatic System and the Circulatory System
    5. The Role of Circulatory System in Body Defence Mechanism
      1. The Body's Defense Mechanism
      2. Immunity and Immunisation
      3. Types of Immunity
      4. HIV and Body's Defense Mechanism
    6. A Healthy Cardiovascular System
    7. Transport of Substances in Plants
      1. Distribution of Vascular System in Dicotyledon Plants
      2. Vascular Tissue in Plant
      3. Vascular System as a Continuous Tube System
      4. Transport of Organic Substances in Plants
      5. Transport of  Water in Plants
      6. The External Conditions that Affect the Rate of Transpiration

    Objective Questions

    1. The Circulatory System (7 Questions) 
    2. The Mechanism of Blood Clotting (3 Questions) 
    3. The Lymphatic System (4 Questions) 
    4. The Role of Circulatory System in Body Defense Mechanism (4 Questions) 


      02 Support and Locomotion

      1. Support and Locomotion in Humans and Animals
        1. The human skeleton
      2. Appreciate a Healthy Musculoskeletal System
      3. Support System in Plants

      Objective Questions

      1. Support and Locomotion in Humans and Animals 1 (6 Questions) 
      2. Support and Locomotion in Humans and Animals 2 (6 Questions) 
      3. Support System in Plants (4 Questions) 


        03 Coordination and Response

        1. Response and Coordination
        2. The Role of Human Nervous System
        3. The Role of Hormones in Humans
        4. Homeostasis in Humans
          1. The human kidney
          2. The formation of urine
        5. Practising a Healthy Lifestyle 
        6. Plant Hormones
          1. The role of auxins in the tropic movements in plants
          2. Ethylene

        Objective Questions

        1. The Role of the Human Nervous System 1 (6 Questions) 
        2. The Role of the Human Nervous System 2 (6 Questions) 
        3. The Role of Hormones in Humans (7 Questions) 
        4. Homeostasis in Humans (7 Questions) 


        04 Reproduction and Growth

        1. Gamete Formation
        2. Role of Hormones in the Menstrual Cycle
        3. Early Development of Zygote in Humans
        4. Contribution of Science and Technology to Human Reproduction
        5. Sexual Reproduction in Flowering Plants
        6. Growth in Multicellular Organisms
        7. Growth Curve
        8. Primary and Secondary Growth in Plants

        Objective Questions

        1. Formation of Gamete (5 Questions) 
        2. Roles of Hormones in the Menstrual Cycle (5 Questions) 


        05 Inheritance

        1. The Concept of Inheritance Based on Mendel's Experiment
        2. Inheritance
        3. Genes and Chromosomes

        Objective Questions

        Inheritance (10 Questions) 



        06 Variation

        1. Variation in Organisms
        2. Cause of Variation
        3. Be Respectful Towards One Another Despite Variation

        Objective Questions

        Variation (9 Questions)

        1.2.1 Angles and Lines II, PT3 Practice

        Posted on by

        1.2.1 Angles and Lines II, PT3 Practice

        Question 1:
        In Diagram below, PQRS, ABQC and KRL are straight lines.
        Find the value of x.

        Solution:
        ∠ K R B + ∠ A B R = 180 o ← Sum of interior angles ∠ K R B + 105 o = 180 o ∠ K R B = 180 o − 105 o ∠ K R B = 75 o ∠ B R Q = 40 o ← Corresponding angle x o = ∠ S R L = ∠ K R Q ← Vertically opposite angle x o = 75 o + 40 o = 115 o x = 115


        Question 2:
        (a) In Diagram below, PQR and SQT are straight lines.
        Find the value of x.

        (b) In Diagram below, PQRS is a straight line. Find the value of x.
        Solution:
        (a)
        ∠ P Q T = ∠ R Q S x o + 90 o = 155 o x o = 155 o − 90 o = 65 o x = 65

        (b)
        ∠ Q R T = 57 o x o + 2 x o = 180 o − 57 o 3 x o = 123 o x o = 123 o 3 x o = 41 o x = 41


        Question 3:
        In Diagram below, PQR is a straight line. Find the value of x.
        Solution:

        x o = ∠ Q R T + ∠ T R S ∠ Q R T = 40 o ∠ T R S = 180 o − 135 o = 45 o Hence, x o = 40 o + 45 o x o = 85 o x = 85


        Question 4:
        In Diagram below, find the value of x.
        Solution:
        40o + 80o + xo + xo = 180o
        2xo = 180o – 120o
        2xo = 60o
        xo = 30o
         x = 30


        Question 5:
        In Diagram below, PQR is an isosceles triangle and QRS is a straight line.
        Find the values of x and y.

        Solution:
        ∠ P R Q = 180 o − 110 o = 70 o ∠ P R Q = ∠ P Q R = 70 o y o = 180 o − 70 o − 70 o = 40 o y = 40 x o = 110 o − 40 o = 70 o x = 70
         
         

        1.1 Angles and Lines II

        Posted on by

        1.1 Angles and Lines II
         
        Identifying Parallel, Transversals, Corresponding Angles, Alternate Angles and Interior Angles
        (A) Parallel lines
        Parallel lines are lines with the same direction. They remain the same distance apart and never meet.


        (B) Transversal lines
        A transversal is a straight line that intersects two or more straight lines.



        (C)         Alternate angles


        (D) Corresponding angles



        (E) Interior angles



        PT3 Smart TIP

        Alternate angles are easily identified by tracing out the pattern “Z” as shown.

        Corresponding angles are easily identified by the pattern “F” as shown.




        Interior angles are easily identified by the pattern “C” as shown.

        Example 1:
        In Diagram below,PQ is parallel to RS. Determine the value of y.

        Solution:

        Construct a line parallel to PQ and passing through W.
        a = 40o and b = 50o← (Alternate angles)
        y = a + b
          = 40o+ 50o
           = 90o


        Example 2:
        In Diagram below, PSQ and STU are straight lines. Find the value of x.
        Solution:
        ∠ W S Q = 180 o − 150 o = 30 o ← Supplementary angle ∠ X T U = ∠ W S Q + ∠ x ← Corresponding angle 75 o = 30 o + ∠ x ∠ x = 75 o − 30 o ∠ x = 45 o x = 45