Question 1:
Diagram 1 shows an experiment to study the relationship between upthrust and the weight of water displaced.
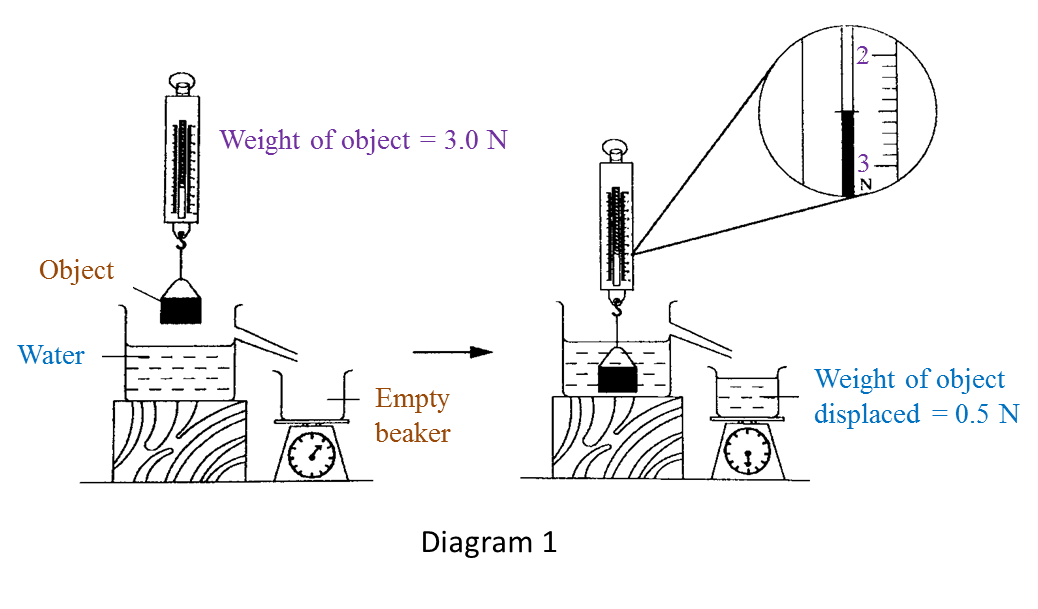
(a) Based on Diagram 1, state the weight of object in water and write down your answer in the Table below. [1 mark]

(b) Observe Diagram 1. Compare the weight of object in the air and in water. [1 mark]
(c) State
one inference for this experiment. [1 mark]
(d) State
one responding variable in this experiment. [1 mark]
(e) The upthrust acts on an object when it is immersed in water.
State the operational definition of upthrust
. [1 mark]
Answer:
(a)

(b) The weight of object in the air is larger than the weight of object in the water.
(c) The apparent loss in weight is equal to the weight of water displaced.
(d) Weight of water displaced.
(e) Upthrust is the apparent loss in weight of an object when it is immersed in water.
Question 2:
Diagram 2.1 shows the weight of a metal block in the air.
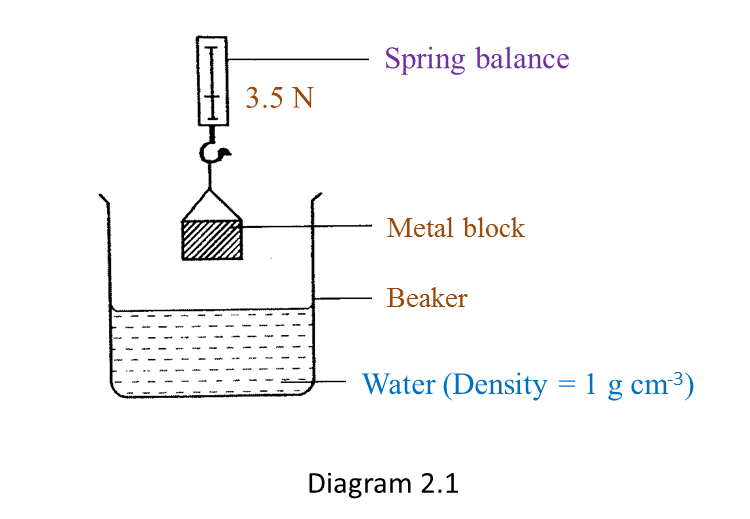
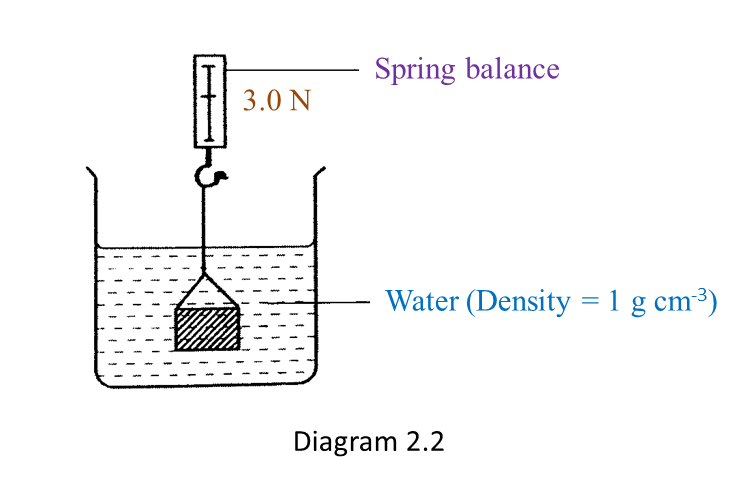
Diagram 2.2 shows the apparent weight of the metal block when it is immersed in water.
(a) Based on Diagram 2.1 and Diagram 2.2:
(i) State
one observation from the result of this experiment. [1 mark]
(ii) State
one inference from this experiment. [1 mark]
(b) State the constant variable in this experiment. [1 mark]
The experiment is repeated by using sea water as shown in Diagram 2.3.
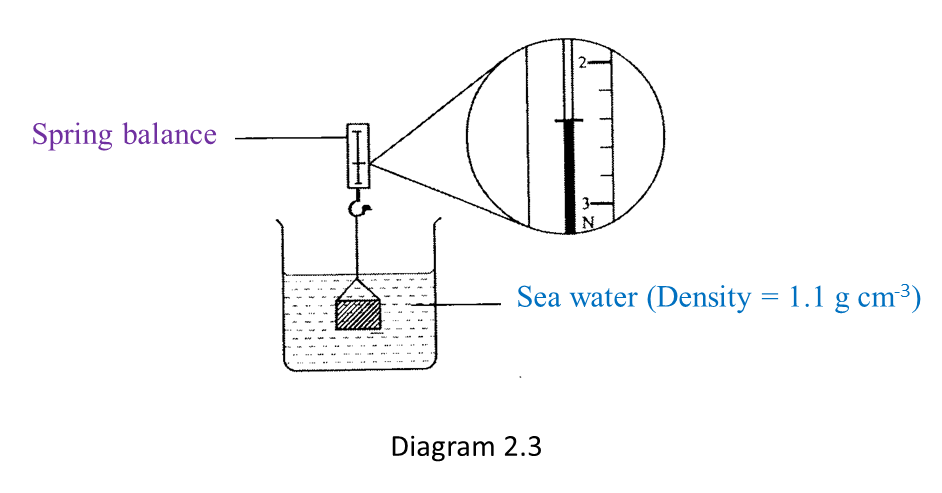
(c) Based on Diagram 2.3, what is the reading on the spring balance? [1 mark]
(d) Predict the reading of the spring balance if the metal block is immersed in a liquid which has higher density than sea water. [1 mark]
Answer:
(a)(i)
The weight of the metal block in air is larger than the apparent weight of the same metal block immersed in water.
(a)(ii)
An upthrust acts on the metal block when it is immersed in water.
(b) Metal block, water (density = 1 g cm
-3). (any one)
(c) 2.4 N
(d) The reading of the spring balance will be lower than the reading shown in Diagram 2.3.
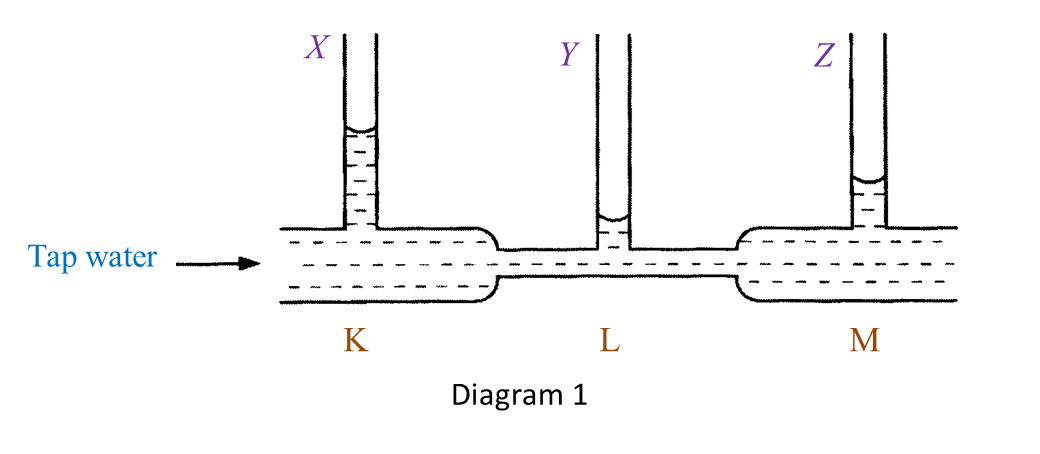






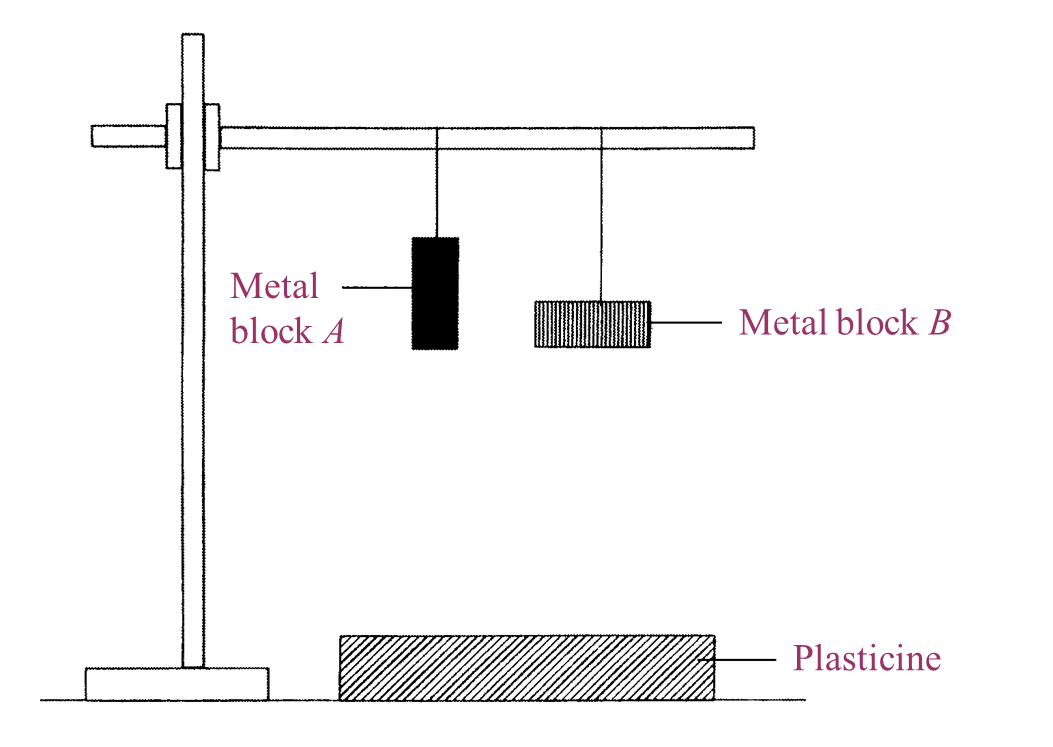 Figure 1.1
Figure 1.1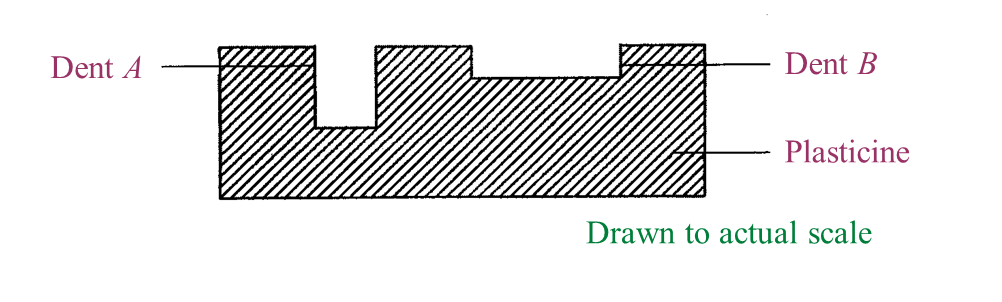 Figure 1.2
Figure 1.2 Figure 1.3
Figure 1.3