Change of Base of Logarithms – Example 5

Posted on May 23, 2020 by Myhometuition

Example 5
Given that

$\log_{2} 3 = 1.585$ and

$\log_{2} 5 = 2.322$ , evaluate the following.
(a)

$\log_{8} 15$
(b)

$\log_{5} 0.6$
(c)

$\log_{15} 30$
(d)

$\log_{16} 45$

Solution:

5.2(a) Example 1 (Logarithms)

Posted on May 22, 2020 by Myhometuition

Example 1
Find the value of each of the following :
(a)

$\log_{2} 64$
(b)

$\log_{3} 1$
(c)

$\log_{5} 5$
(d)

$\log_{\frac{1}{2}} 4$
(e)

$\log_{8} 0.25$

Example 2
Solve the following equations:
(a)

$\log_{3} 5 x = 2$
(b)

$\log_{x + 1} 81 = 2$
(c)

$\log_{x} 5 x - 6 = 2$

SPM Practice (Paper 1)

Posted on May 22, 2020 by Myhometuition

Question 14:

$Show that 6 x - 6 - 2 k x^{2} = x^{2} has no real roots if k > \frac{1}{4} .$

Solution:

Question 15:
The quadratic equation

$x^{2} + p x + q = 0$ has roots –2 and 6. Find
(a) the value of p and of q,
(b) the range of values of r for which the equation

$x^{2} + p x + q = r$ has no real roots.

Solution:

SPM Practice (Paper 1)

Posted on May 22, 2020 by Myhometuition

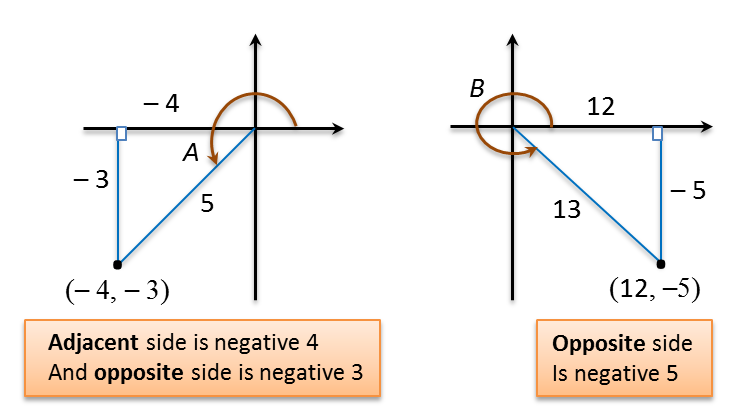
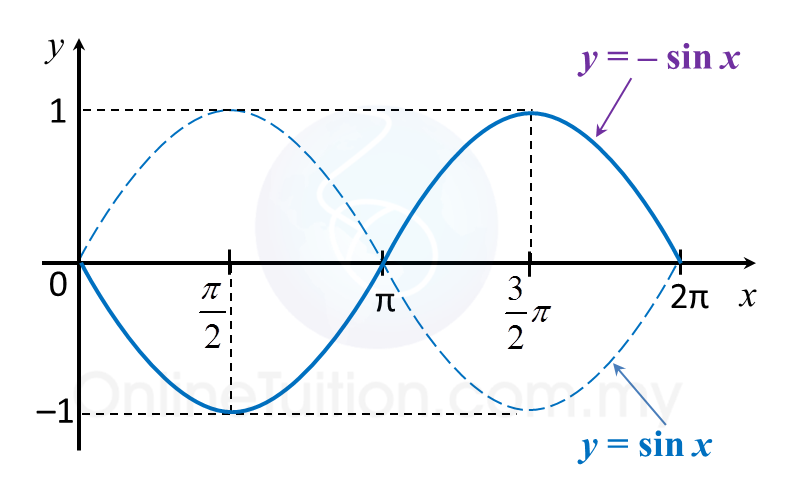
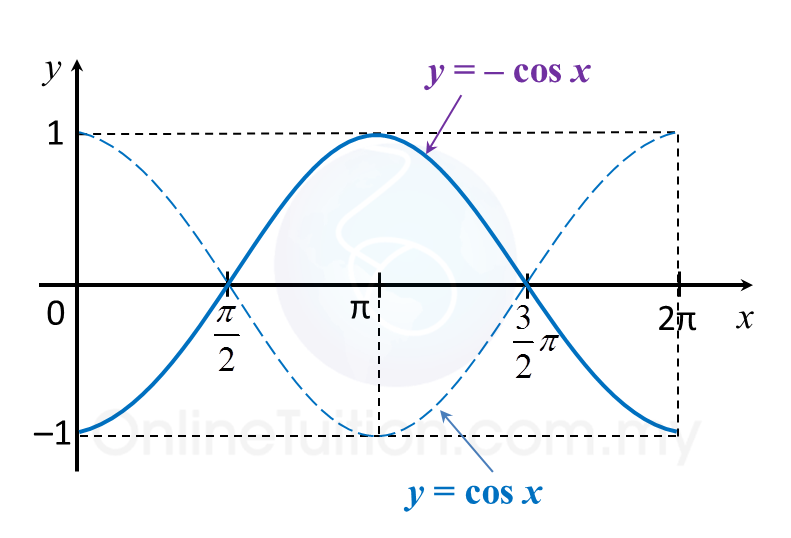
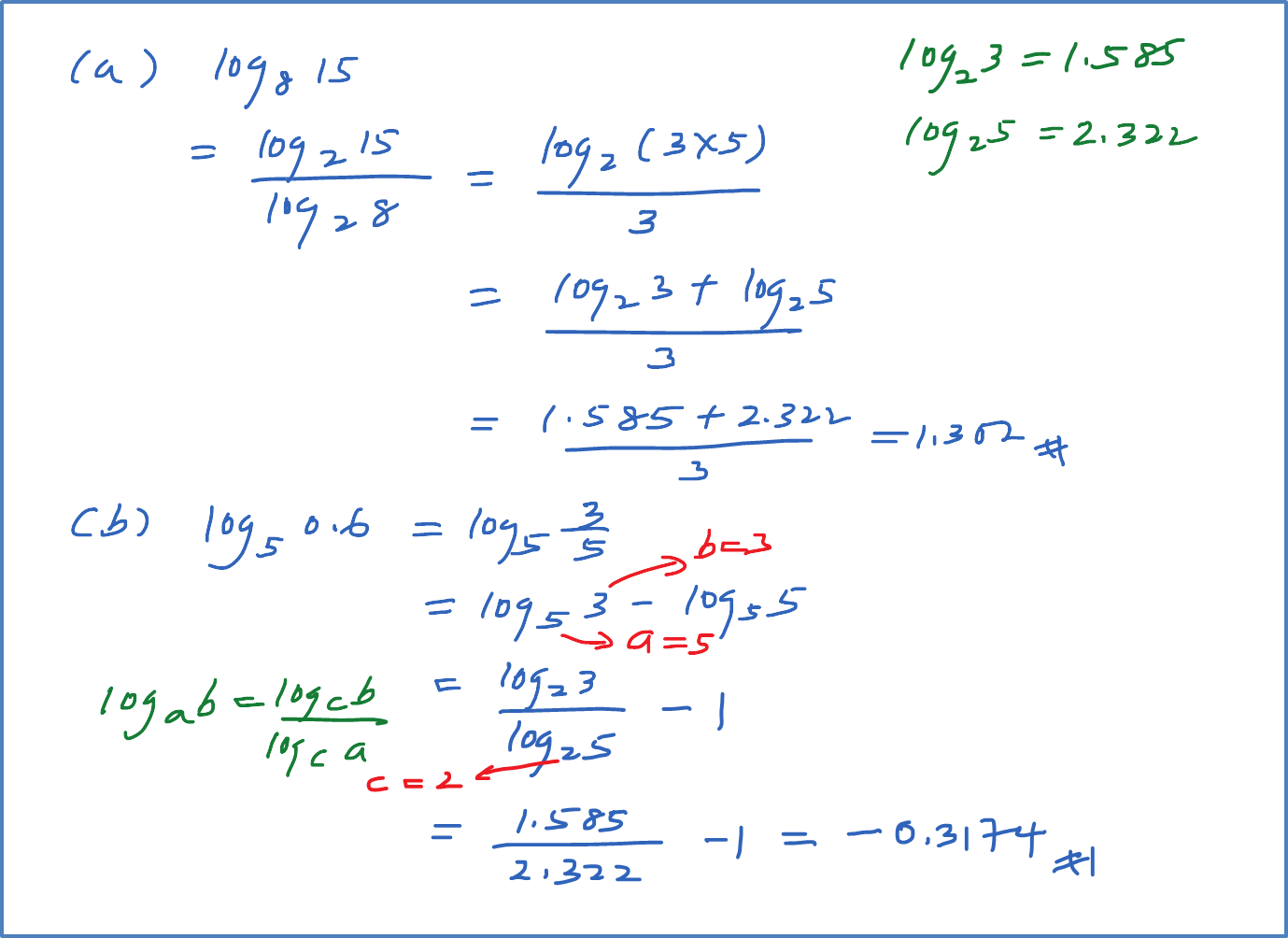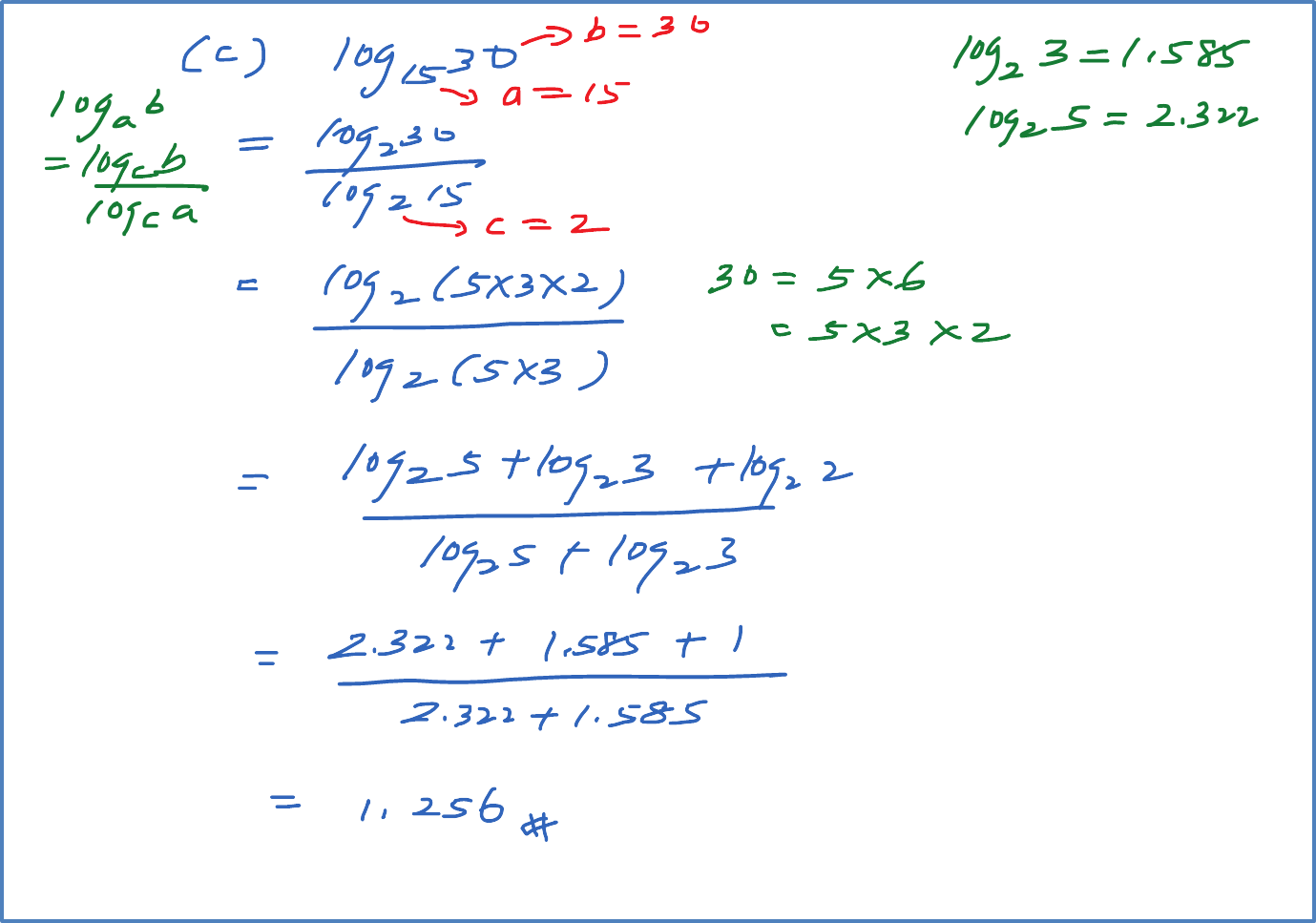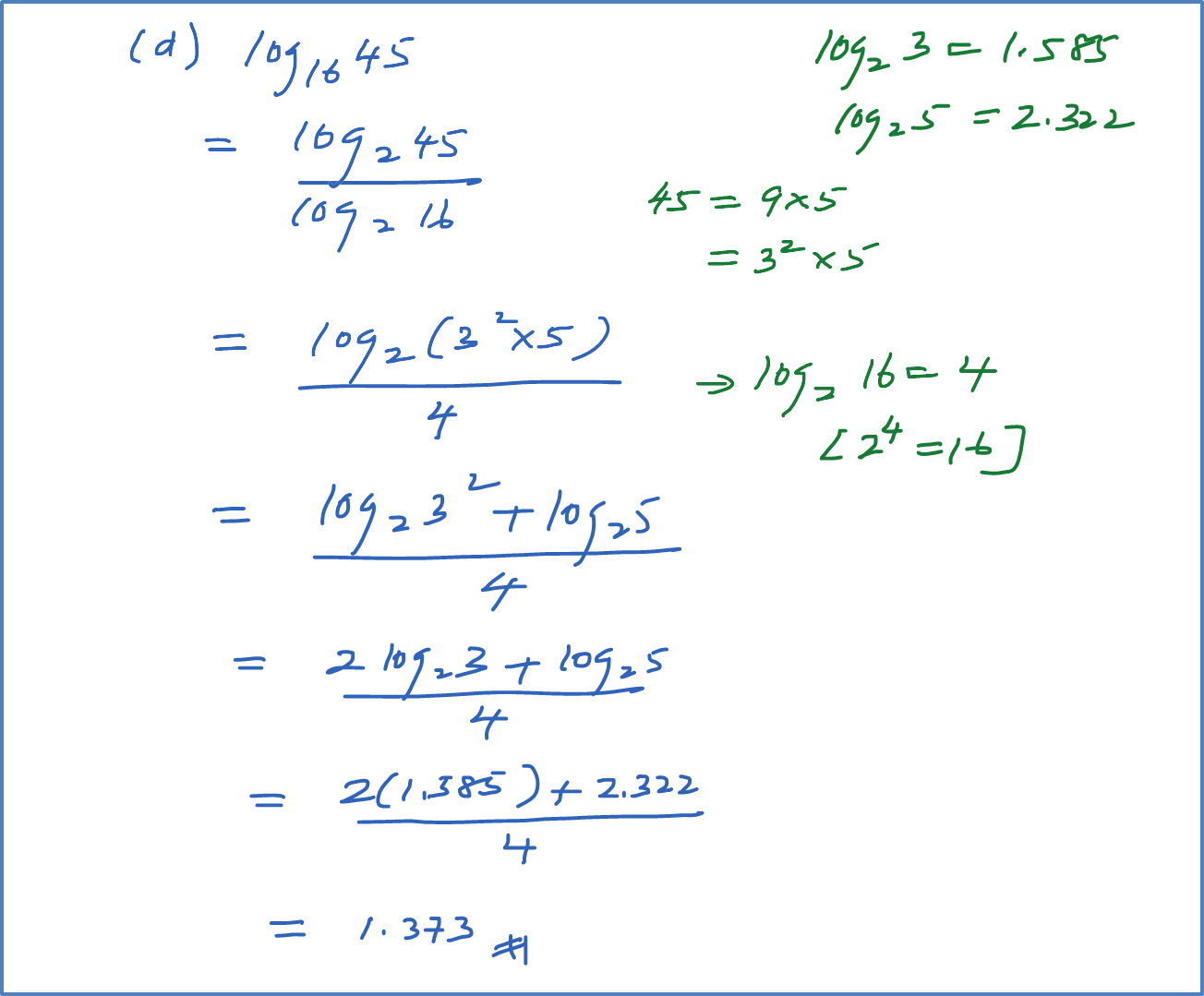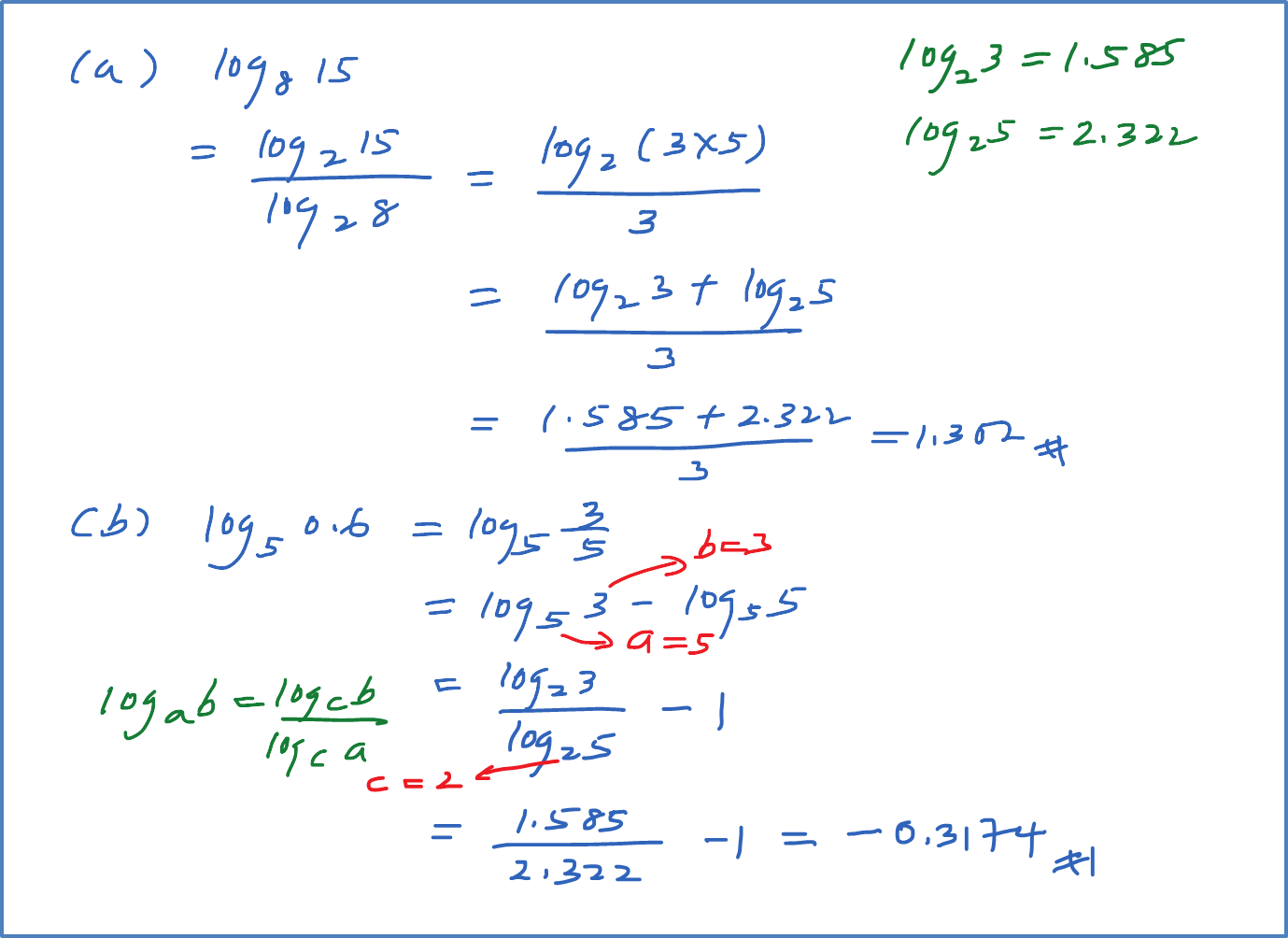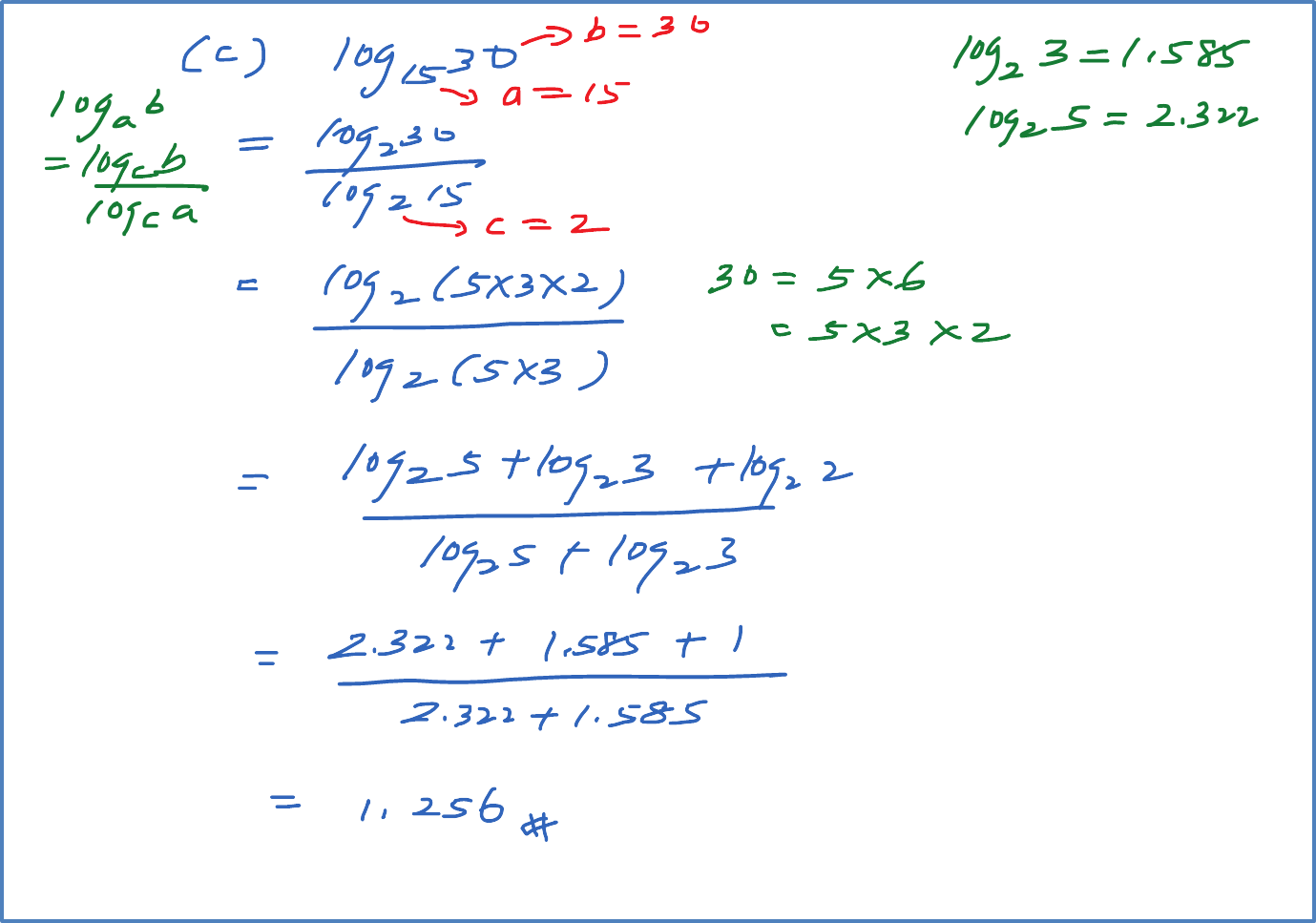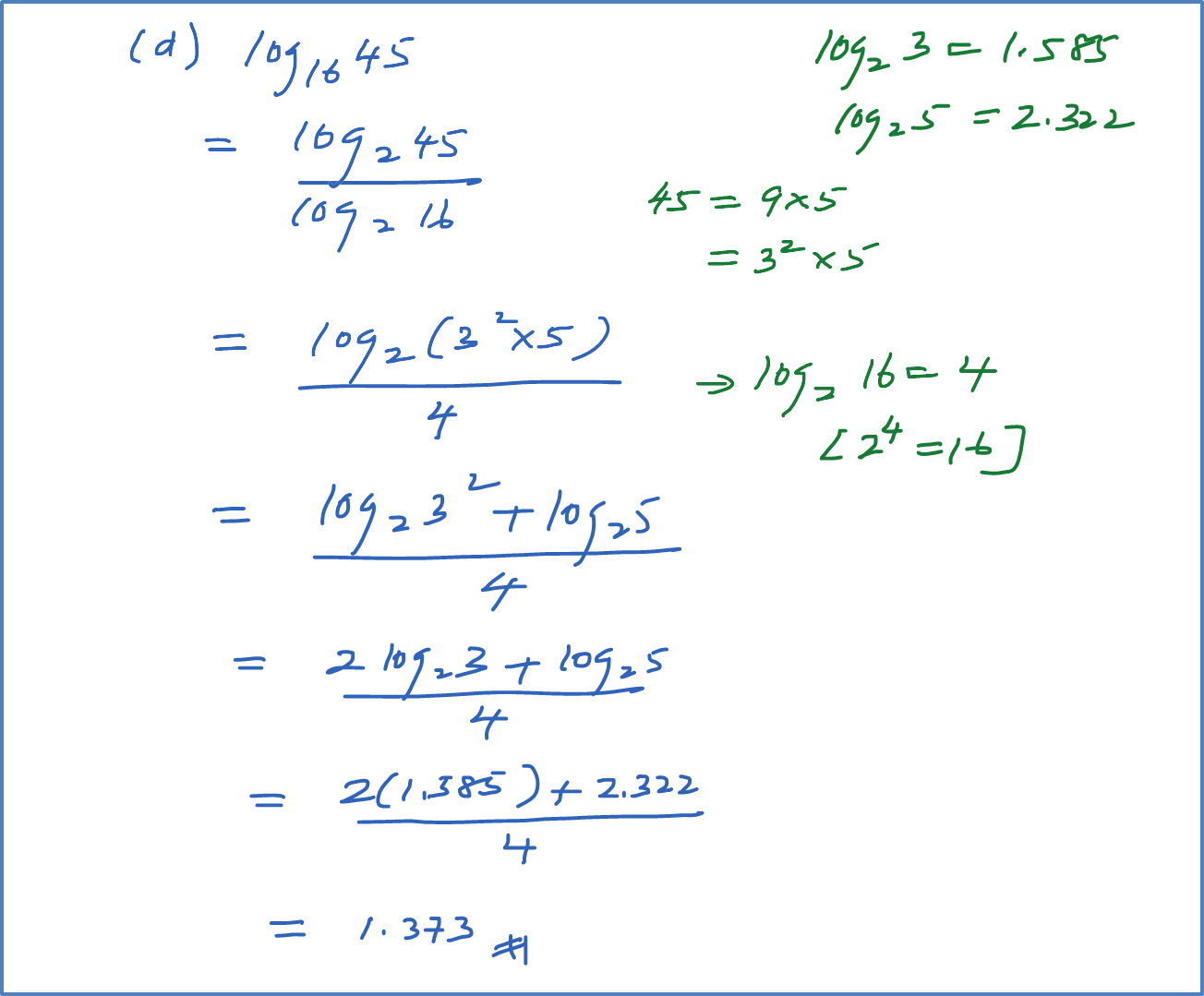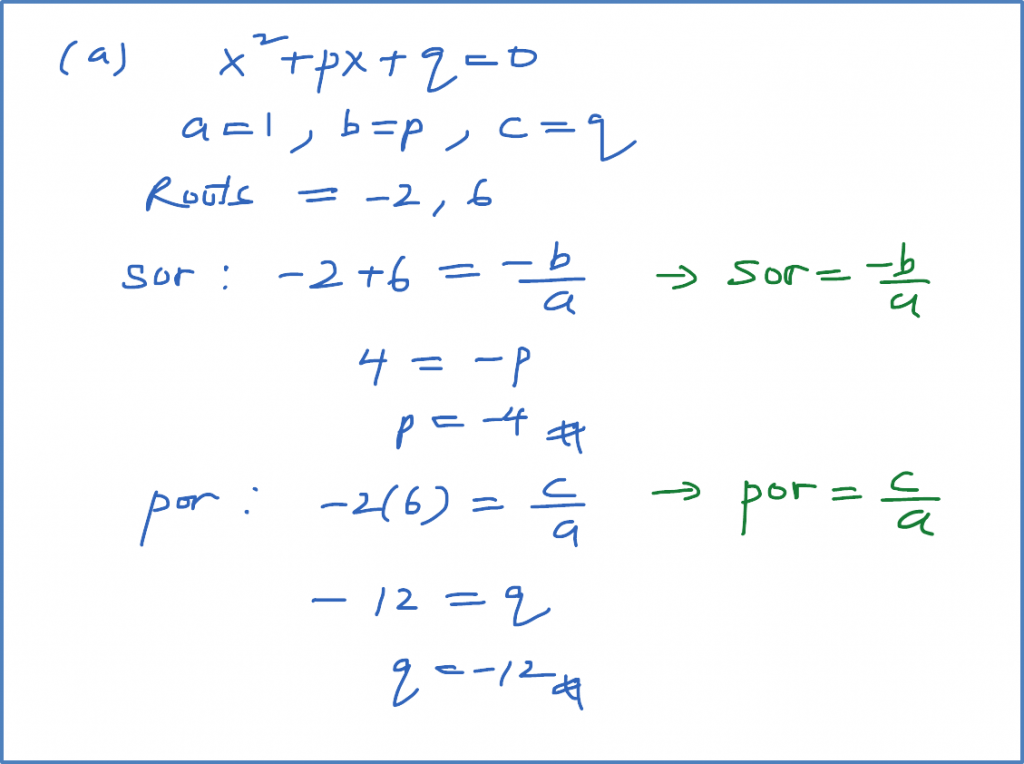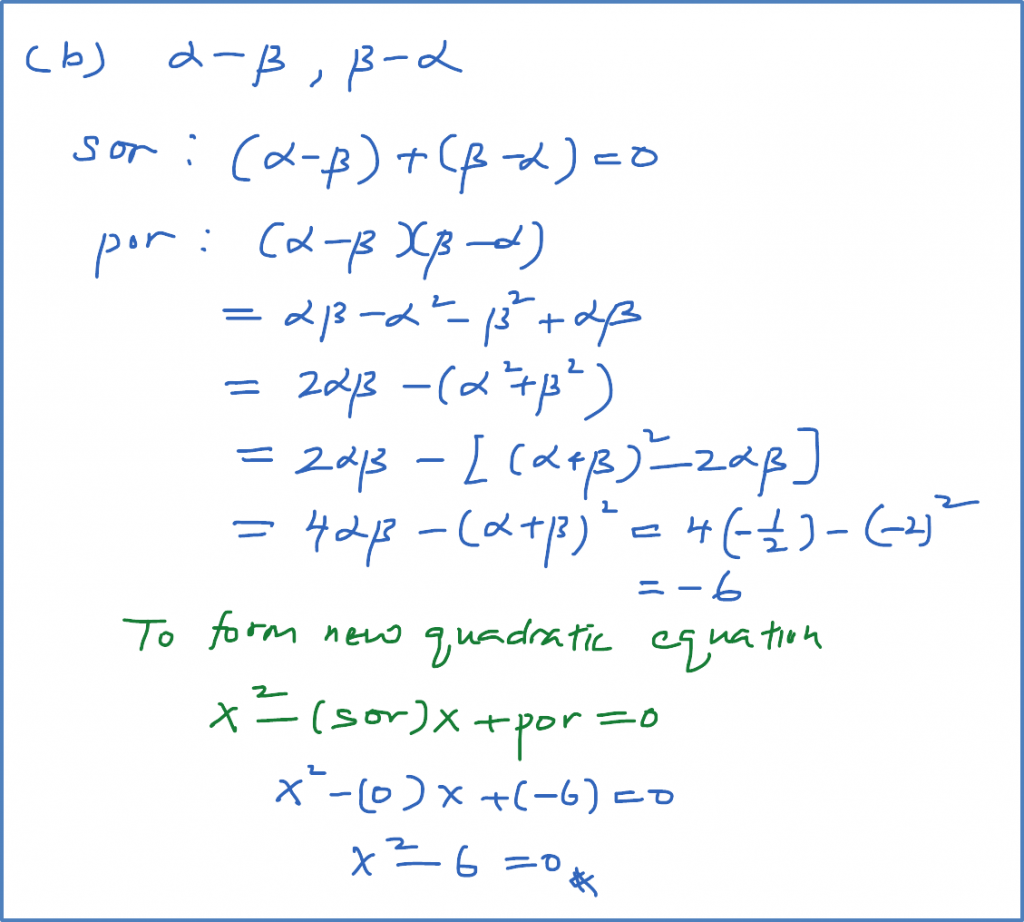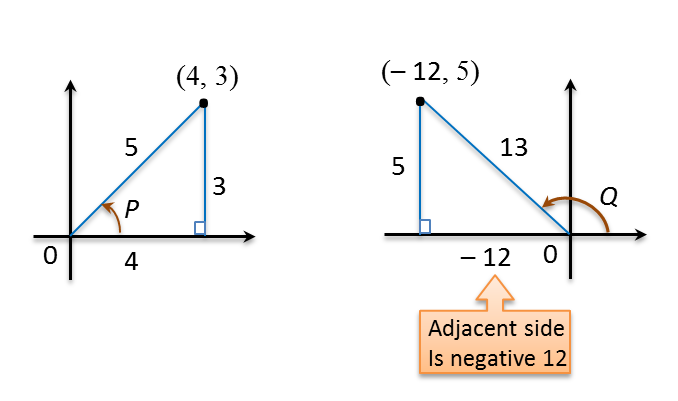Question 9:
The roots of the equation

$6 x^{2} + h x + 1 = 0 are α and β, whereas 3 α and 3 β$ are the roots of the equation

$2 x^{2} - x + k = 0$ . Find the value of h and k.

Solution:

$\begin{array}{l} 6 x^{2} + h x + 1 = 0 \\ a = 6, b = h, c = 1 \\ Roots = α, β \\ sor : \\ α + β = - \frac{b}{a} \\ α + β = - \frac{h}{6} ......... (1) \\ p o r : \\ α β = \frac{c}{a} \\ α β = \frac{1}{6} ......... (2) \\ 2 x^{2} - x + k = 0 \\ a = 2, b = - 1, c = k \\ Roots = 3 α, 3 β \\ sor : \\ 3 α + 3 β = - \frac{b}{a} \\ 3 (α + β) = - \frac{(- 1)}{2} \\ α + β = \frac{1}{6} ......... (3) \\ p o r : \\ 3 α (3 β) = \frac{c}{a} \\ 9 α β = \frac{k}{2} \\ k = 18 α β ......... (4) \\ Substitute (3) into (1) \\ α + β = - \frac{h}{6} \\ \frac{1}{6} = - \frac{h}{6} \\ h = - 1 \\ Substitute (2) into (4) \\ k = 18 α β \\ k = 18 (\frac{1}{6}) \\ k = 3 \end{array}$

Question 10:
Find the range of values of p for which the equation

$2 x^{2} + 5 x + 3 - p = 0$ has two real distinct roots.

Solution:

SPM Practice (Paper 1)

Posted on May 22, 2020 by Myhometuition

Question 3:
Solve the following quadratic equations by using quadratic formula. Give your answer in four significant figures.

$\begin{array}{l} (a) (x + 1) (x - 5) = 15 \\ (b) \frac{x^{2} + 3 x - 2}{x^{2} - x - 1} = 3 \end{array}$

Solution:

Question 4:
If the roots of

$2 x^{2} + 4 x - 1 = 0 are α and β,$ find the equations whose roots are

$\begin{array}{l} (a) α^{2}, β^{2} \\ (b) α - β, β - α \end{array}$

Solution:

Question 5:
Write and simplify the equation whose roots are double the roots of

$3 x^{2} - 5 x - 1 = 0$ , without solving the given equation.

Solution:

5.5.1a Proving Trigonometric Identities Using Addition Formula And Double Angle Formulae (Part 2)

Posted on May 22, 2020 by Myhometuition

Example 3:

(a) Given that

$\sin P = \frac{3}{5} and \sin Q = \frac{5}{13},$ such that P is an acute angle and Q is an obtuse angle, without using tables or a calculator, find the value of cos (P + Q).

(b) Given that

$\sin A = - \frac{3}{5} and \sin B = \frac{12}{13},$ such that A and B are angles in the third and fourth quadrants respectively, without using tables or a calculator, find the value of sin (A – B).

Solution:

(a)

$\begin{array}{l} \sin P = \frac{3}{5}, \cos P = \frac{4}{5} \\ \sin Q = \frac{5}{13}, \cos Q = - \frac{12}{13} \\ \cos (P + Q) \\ = \cos A \cos B - \sin A \sin B \\ = (\frac{4}{5}) (- \frac{12}{13}) - (\frac{3}{5}) (\frac{5}{13}) \\ = - \frac{48}{65} - \frac{15}{65} \\ = - \frac{63}{65} \end{array}$

(b)

$\begin{array}{l} \sin A = - \frac{3}{5}, \cos A = - \frac{4}{5} \\ \sin B = - \frac{5}{13}, \cos B = \frac{12}{13} \\ s i n (A - B) \\ = s i n A \cos B - c o s A \sin B \\ = (- \frac{3}{5}) (\frac{12}{13}) - (- \frac{4}{5}) (- \frac{5}{13}) \\ = - \frac{36}{65} - \frac{20}{65} \\ = - \frac{56}{65} \end{array}$

5.3.3 Sketching Graphs of Trigonometric Functions (Part 2)

Posted on May 22, 2020 by Myhometuition

5.3.3 Sketching Graphs of Trigonometric Functions

Example 1:

Sketch the graph of each of the following trigonometric functions for π ≤ x ≤ 2π.

(g) y = –sin x
(h) y = –cos x

(i) y = | sin x |
(j) y = | cos x |

(k) y = tan 2x

Solution:

(g)

(h)

(i)

(j)

(k)

8.2b Standard Normal Distribution Tables (Example 2)

Posted on May 21, 2020 by Myhometuition

8.2b Standard Normal Distribution Tables (Example 2)

Example 2:

Find the value of each of the following probabilities by reading the standard normal distribution tables.

(a) P (0.4 < Z < 1.2)

(b) P (–1 < Z < 2.5)

Solution:

(a)

P (0.4 < Z < 1.2)

= Area P – Area Q

= Q (0.4) – Q (1.2) ← (reading from the standard normal distribution table for 0.4 and 1.2 are 0.3446 and 0.1151 respectively)

= 0.3446 – 0.1151

= 0.2295

(b)

P (–1 < Z < 2.5)

= 1– Area P – Area Q

= 1 – Q (1) – Q (2.5)

= 1 – 0.1587 – 0.00621 ← (reading from the standard normal distribution table for 1 and 2.5 are 0.1587 and 0.00621 respectively)

= 0.8351

(c)

P (–1.3 < Z < –0.5)

= Area P – Area Q

= Q (0.5) – Q (1.3)

= 0.3085 – 0.0968 ← (reading from the standard normal distribution table for 0.5 and 1.3 are 0.3085 and 0.0968 respectively)

= 0.2117

8.2c Probability of an Event

Posted on May 21, 2020 by Myhometuition

8.2c Probability of an Event

Example:

The masses of pears in a fruit stall are normally distributed with a mean of 220 g and a variance of 100 g. Find the probability that a pear that is picked at random has a mass

(a) of more than 230 g.

(b) between 210 g and 225 g.

Hence, find the value of h such that 90% of the pears weigh more than h g.

Solution:

µ = 220 g

σ = √100 = 10 g

Let X be the mass of a pear.

(a)

$\begin{array}{l} P (X > 230) \\ = P (Z > \frac{230 - 220}{10}) \leftarrow \begin{array}{l} Convert to standard normal \\ distribution using Z = \frac{X - μ}{σ} \end{array} \\ = P (Z > 1) \\ = 0.1587 \end{array}$

(b)

$\begin{array}{l} P (210 < X < 225) \\ = P (\frac{210 - 220}{10} < Z < \frac{225 - 220}{10}) \leftarrow \begin{array}{l} Convert to standard normal \\ distribution using Z = \frac{X - μ}{σ} \end{array} \\ = P (- 1 < Z < 0.5) \\ = 1 - P (Z > 1) - P (Z > 0.5) \\ = 1 - 0.1587 - 0.3085 \\ = 0.5328 \end{array}$

For 90% (probability = 0.9) of the pears weigh more than h g,

P (X > h) = 0.9

P (X < h) = 1 – 0.9

= 0.1

From the standard normal distribution table,

P (Z > 0.4602) = 0.1

P (Z < –0.4602) = 0.1