Soalan 10 (3 markah):
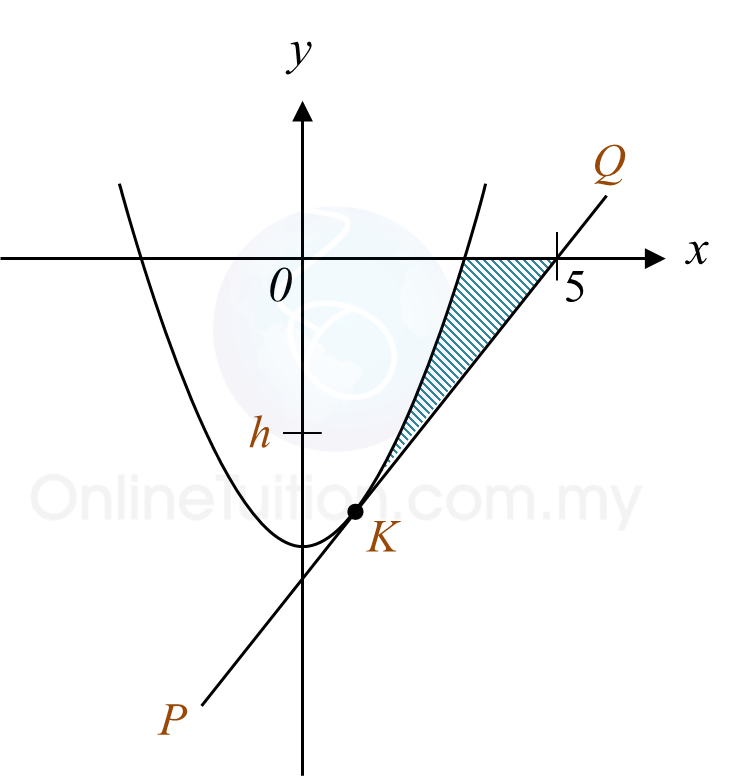
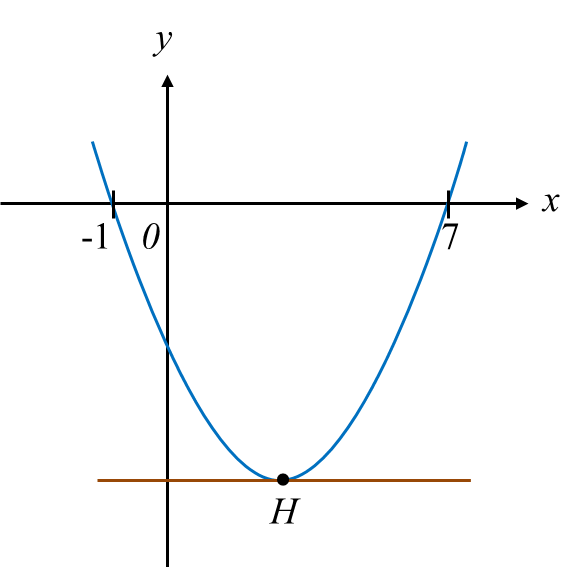
Rajah menunjukkan graf y = a (x – p)2 + q, dengan keadaan a, p dan q ialah pemalar. Garis lurus y = –8 ialah tangen kepada lengkung pada titik H.
 Rajah
Rajah
(a) Nyatakan koordinat H.
(b) Cari nilai a.
Penyelesaian:
(a)
(b)
Rajah menunjukkan graf y = a (x – p)2 + q, dengan keadaan a, p dan q ialah pemalar. Garis lurus y = –8 ialah tangen kepada lengkung pada titik H.
 Rajah
Rajah(a) Nyatakan koordinat H.
(b) Cari nilai a.
Penyelesaian:
(a)
(b)
Soalan 11 (3 markah):
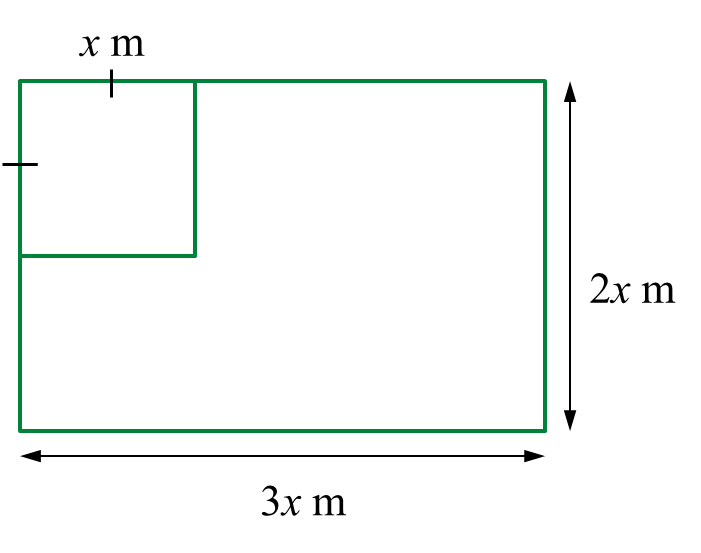
Faizal mempunyai sekeping papan lapis berbentuk segi empat tepat yang berukuran 3x meter panjang dan 2x meter lebar. dia memotong sebahagian daripada papan lapis itu kepada bentuk segi empat sama yang bersisi x meter untuk membuat permukaan meja.
Cari julat nilai x jika luas papan lapis yang tinggal adalah sekurang-kurangnya (x2 + 4) meter2.
Penyelesaian:
Luas papan berlapis – luas segi empat sama ≥ (x2 + 4)
3x(2x) – x2 ≥ x2 + 4
6x2 – x2 – x2 ≥ 4
4x2 ≥ 4
x2 – 1 ≥ 0
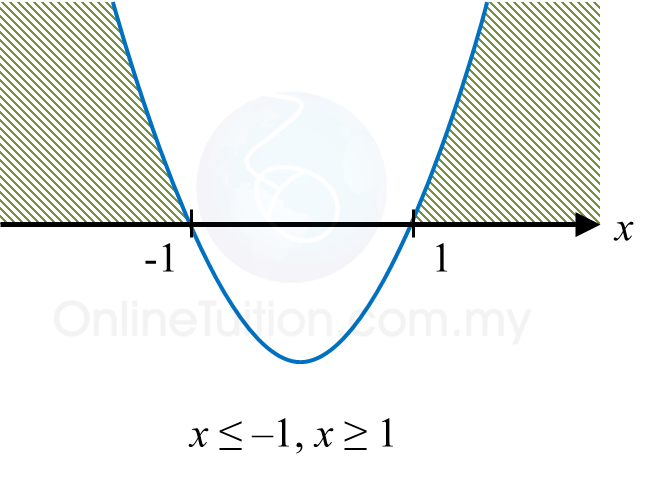
(x + 1)(x – 1) ≥ 0
x ≤ –1 or x ≥ 1
Maka, x ≥ 1 (panjang > 0)
Faizal mempunyai sekeping papan lapis berbentuk segi empat tepat yang berukuran 3x meter panjang dan 2x meter lebar. dia memotong sebahagian daripada papan lapis itu kepada bentuk segi empat sama yang bersisi x meter untuk membuat permukaan meja.
Cari julat nilai x jika luas papan lapis yang tinggal adalah sekurang-kurangnya (x2 + 4) meter2.
Penyelesaian:

Luas papan berlapis – luas segi empat sama ≥ (x2 + 4)
3x(2x) – x2 ≥ x2 + 4
6x2 – x2 – x2 ≥ 4
4x2 ≥ 4
x2 – 1 ≥ 0
(x + 1)(x – 1) ≥ 0
x ≤ –1 or x ≥ 1
Maka, x ≥ 1 (panjang > 0)

 Rajah
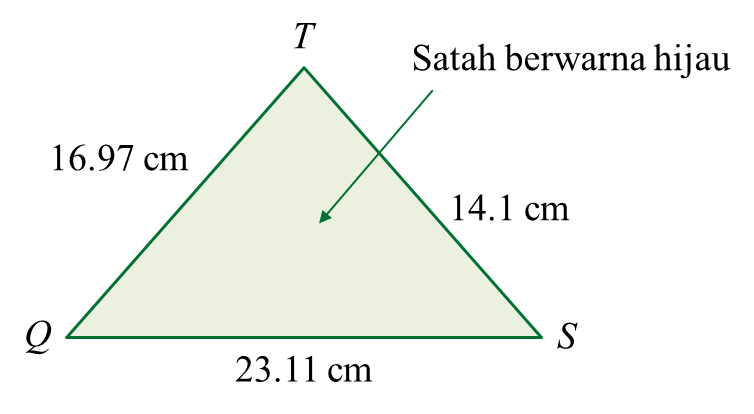
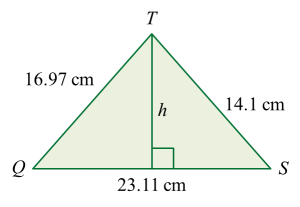
Rajah 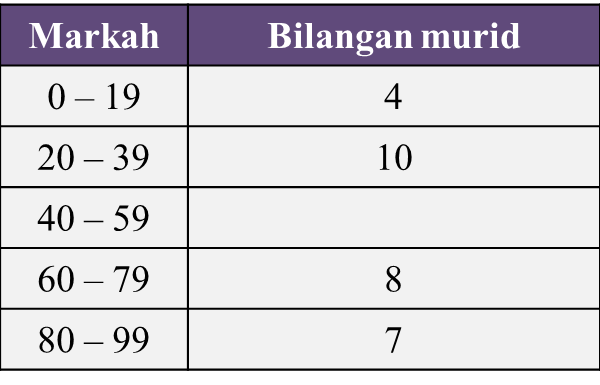 Jadual
Jadual
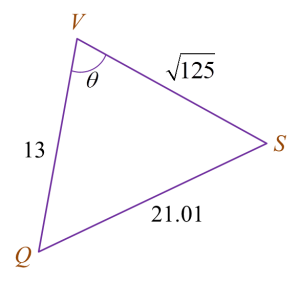
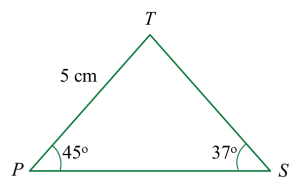
 Diberi bahawa ∠PST = 37o dan ∠TPS = 45o.
Diberi bahawa ∠PST = 37o dan ∠TPS = 45o.