Soalan 10 (8 markah):
Rajah menunjukkan bulatan dan sektor sebuah bulatan dengan pusat sepunya O. Jejari bulatan ialah r cm.
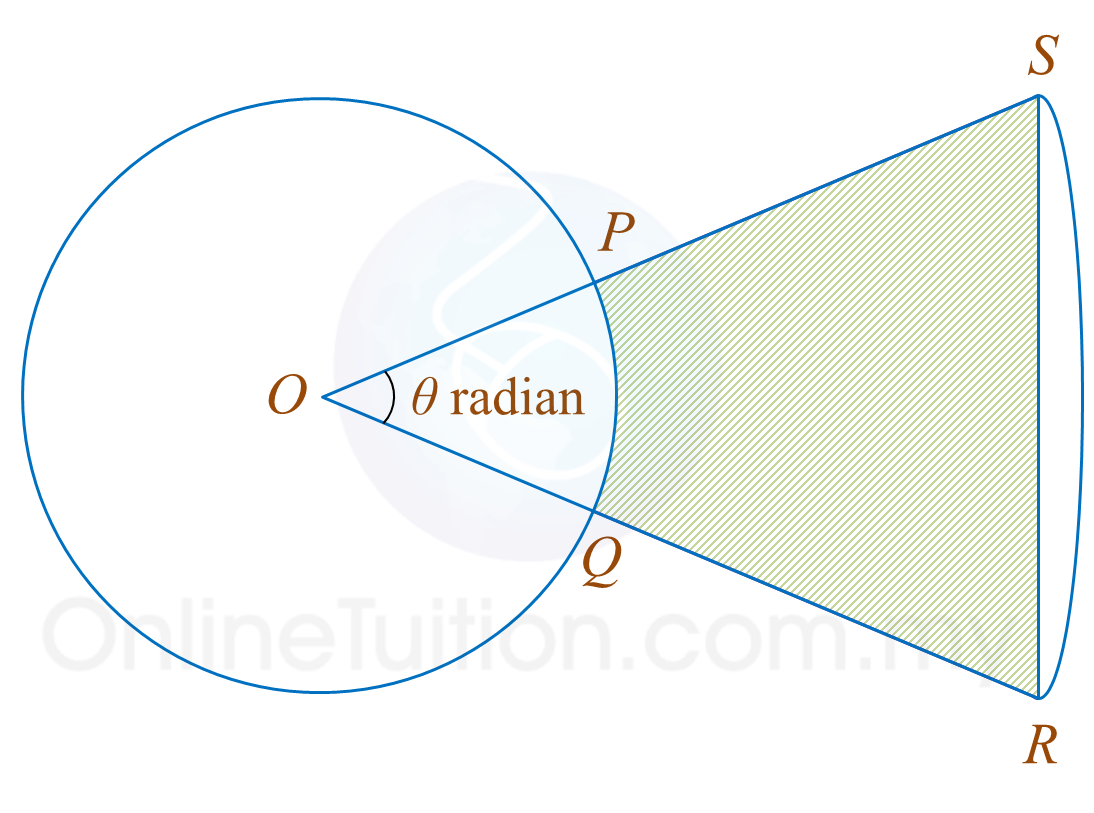
Diberi bahawa panjang lengkok PQ dan lengkok RS masing-masing ialah 2 cm dan 7 cm. QR = 10 cm.
[Guna θ = 3.142]
Cari
(a) nilai r dan nilai θ,
(b) luas, dalam cm2, kawasan yang berlorek.
Penyelesaian:
(a)
(b)
Rajah menunjukkan bulatan dan sektor sebuah bulatan dengan pusat sepunya O. Jejari bulatan ialah r cm.

Diberi bahawa panjang lengkok PQ dan lengkok RS masing-masing ialah 2 cm dan 7 cm. QR = 10 cm.
[Guna θ = 3.142]
Cari
(a) nilai r dan nilai θ,
(b) luas, dalam cm2, kawasan yang berlorek.
Penyelesaian:
(a)
(b)


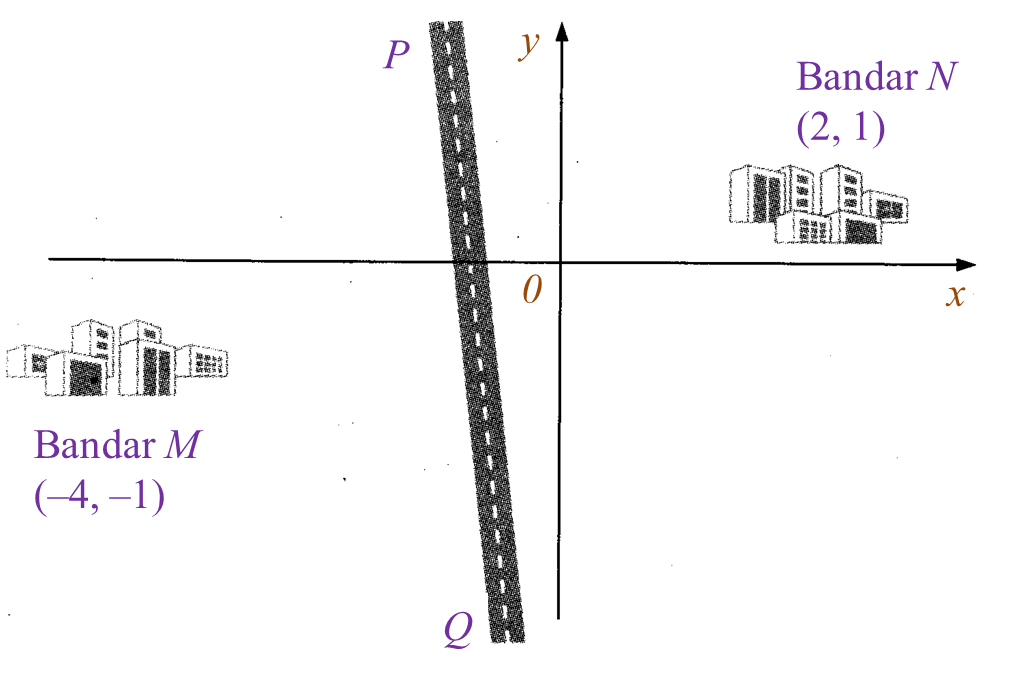
 Rajah 1
Rajah 1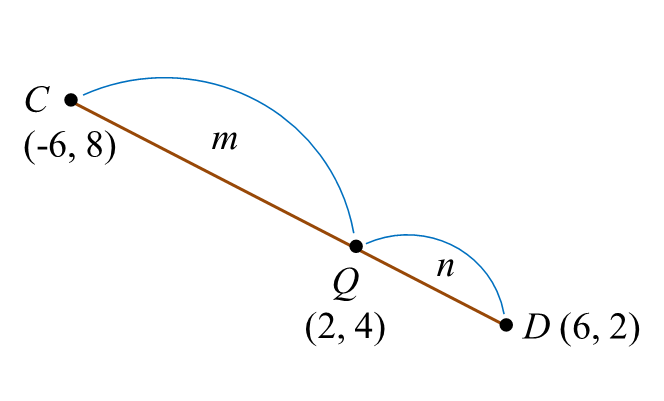
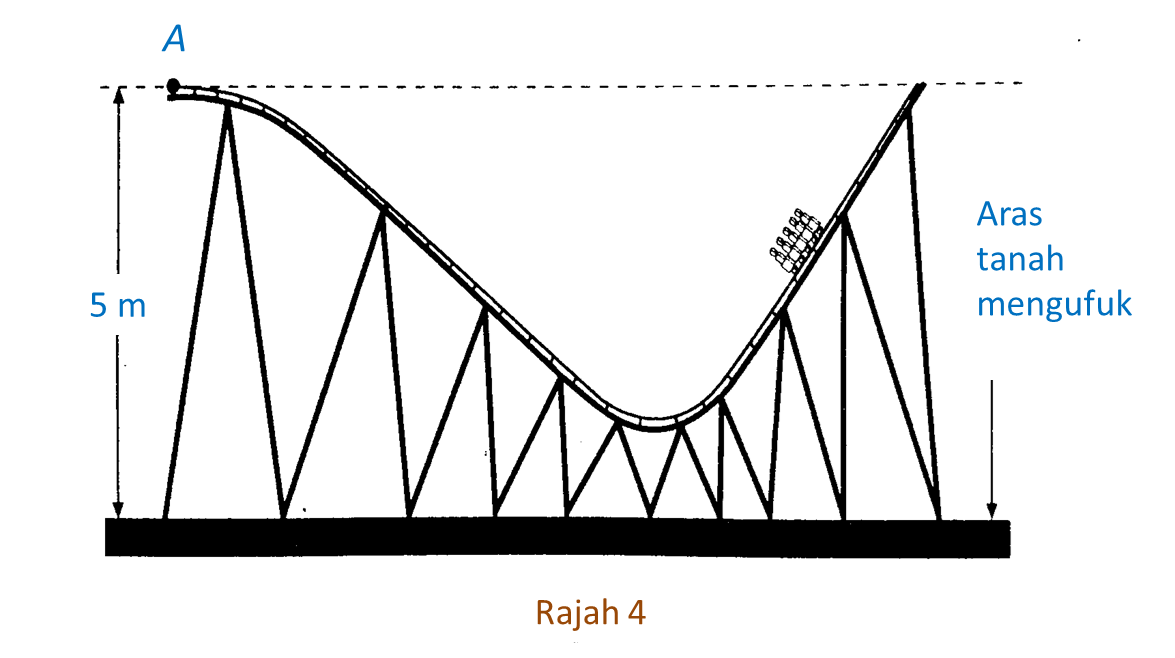
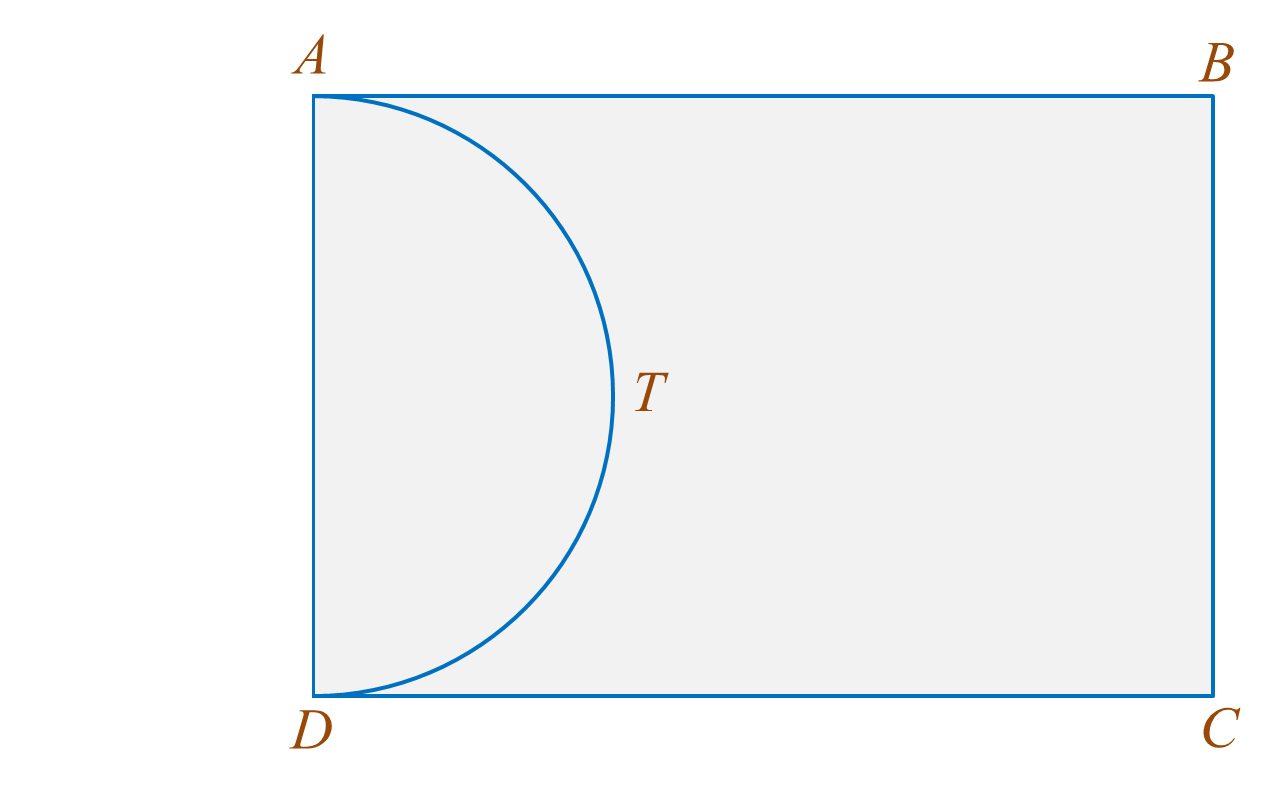 Diberi bahawa DC = 6y meter dan BC = 7x meter, x ≠ y. Luas taman berbentuk segi empat tepat ABCD ialah 168 meter2 dan perimeter kawasan berumput ialah 60 meter. Kolam dengan kedalaman seragam mengandungi 15.4 meter3 air.
Diberi bahawa DC = 6y meter dan BC = 7x meter, x ≠ y. Luas taman berbentuk segi empat tepat ABCD ialah 168 meter2 dan perimeter kawasan berumput ialah 60 meter. Kolam dengan kedalaman seragam mengandungi 15.4 meter3 air.

