6.8.7 Geometri Koordinat, SPM Praktis (Kertas 2)
Soalan 7:
Penyelesaian secara lukisan berskala tidak diterima.
Rajah di bawah menunjukkan segi tiga PRS. Sisi PR bersilang dengan paksi-y pada titik Q.
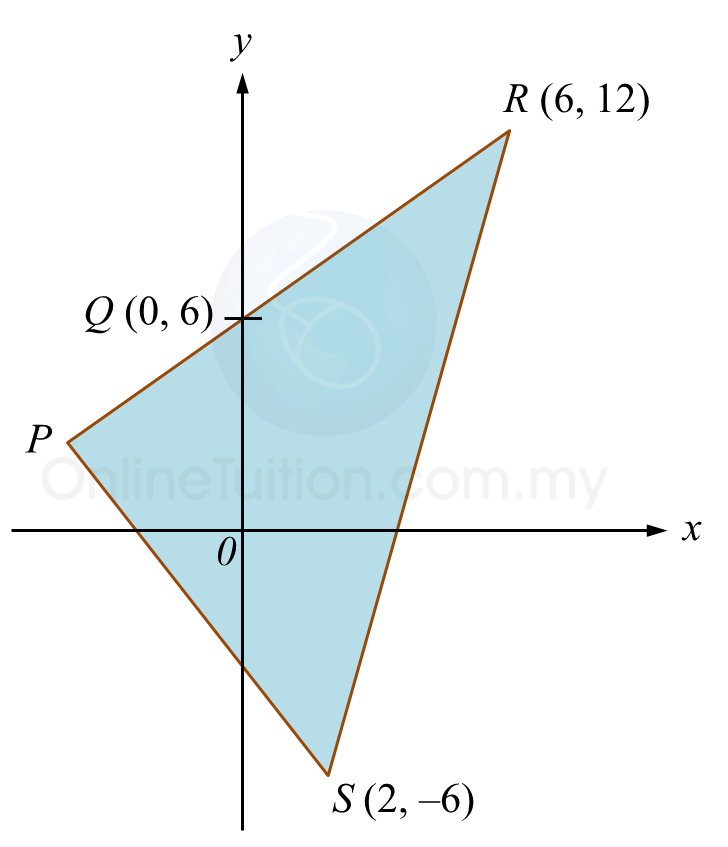
(a) Diberi PQ : QR = 2 : 3, cari
(i) koordinat P,
(ii) persamaan garis lurus PS,
(iii) luas, dalam unit2, segi tiga PRS.
(b) Titik M bergerak dengan keadaan jaraknya dari titik R adalah sentiasa dua kali jaraknya dari titik S.
Cari persamaan lokus M.
Penyelesaian:
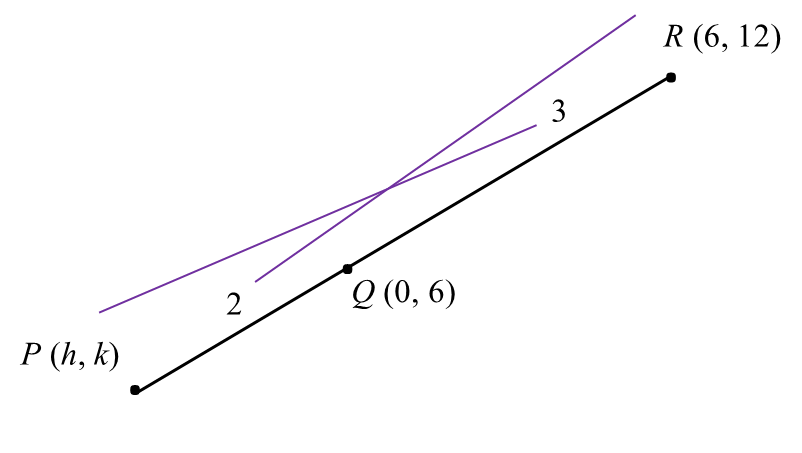 P=(2(6)+3h2+3,2(12)+3k2+3)(0,6)=(12+3h5,24+3k5)12+3h5=0 3h=−12 h=−424+3k5=63k=30−24k=2P=(−4,2)
P=(2(6)+3h2+3,2(12)+3k2+3)(0,6)=(12+3h5,24+3k5)12+3h5=0 3h=−12 h=−424+3k5=63k=30−24k=2P=(−4,2)
(a)(ii)
mPS=2−(−6)−4−2 =−86 =−43Persamaan PS:y−y1=−43(x−2)y−(−6)=−43x+833y+18=−4x+83y=−4x−10
(a)(iii)
Luas △ PRS=12|−4 2 6 2 −6 12 −42|=12|(24+24+12)−(4−36−48)|=12|60−(−80)|=70 unit2
(b)
Katakan P=(x,y)MR=2MS√(x−6)2+(y−12)2=2√(x−2)2+(y+6)2(x−6)2+(y−12)2=4[(x−2)2+(y+6)2]x2−12x+36+y2−24y+144=4[x2−4x+4+y2+12y+36]x2−12x+y2−24y+180=4x2−16x+4y2+48y+1603x2+3y2−4x+72y−20=0
Soalan 7:
Penyelesaian secara lukisan berskala tidak diterima.
Rajah di bawah menunjukkan segi tiga PRS. Sisi PR bersilang dengan paksi-y pada titik Q.

(a) Diberi PQ : QR = 2 : 3, cari
(i) koordinat P,
(ii) persamaan garis lurus PS,
(iii) luas, dalam unit2, segi tiga PRS.
(b) Titik M bergerak dengan keadaan jaraknya dari titik R adalah sentiasa dua kali jaraknya dari titik S.
Cari persamaan lokus M.
Penyelesaian:
(a)(i)
 P=(2(6)+3h2+3,2(12)+3k2+3)(0,6)=(12+3h5,24+3k5)12+3h5=0 3h=−12 h=−424+3k5=63k=30−24k=2P=(−4,2)
P=(2(6)+3h2+3,2(12)+3k2+3)(0,6)=(12+3h5,24+3k5)12+3h5=0 3h=−12 h=−424+3k5=63k=30−24k=2P=(−4,2)
(a)(ii)
mPS=2−(−6)−4−2 =−86 =−43Persamaan PS:y−y1=−43(x−2)y−(−6)=−43x+833y+18=−4x+83y=−4x−10
(a)(iii)
Luas △ PRS=12|−4 2 6 2 −6 12 −42|=12|(24+24+12)−(4−36−48)|=12|60−(−80)|=70 unit2
(b)
Katakan P=(x,y)MR=2MS√(x−6)2+(y−12)2=2√(x−2)2+(y+6)2(x−6)2+(y−12)2=4[(x−2)2+(y+6)2]x2−12x+36+y2−24y+144=4[x2−4x+4+y2+12y+36]x2−12x+y2−24y+180=4x2−16x+4y2+48y+1603x2+3y2−4x+72y−20=0
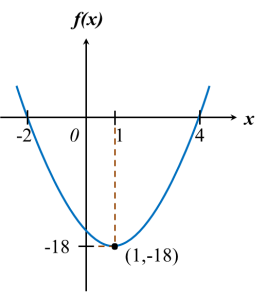



 Rajah
Rajah