Soalan 13:
Diberi fungsi g(x) = 3x dan h(x) = m – nx, dengan keadaan m dan n ialah pemalar.
Ungkapkan m dalam sebutan n dengan keadaan hg(1) = 4.
Penyelesaian:
hg(x)=h(3x) =m−n(3x) =m−3nxhg(1)=4m−3n(1)=4m−3n=4m=4+3n
Diberi fungsi g(x) = 3x dan h(x) = m – nx, dengan keadaan m dan n ialah pemalar.
Ungkapkan m dalam sebutan n dengan keadaan hg(1) = 4.
Penyelesaian:
hg(x)=h(3x) =m−n(3x) =m−3nxhg(1)=4m−3n(1)=4m−3n=4m=4+3n
Soalan 14:
Diberi fungsi g : x → 3x – 2, cari
(a) nilai x apabila g(x) memeta kepada diri sendiri,
(b) nilai k dengan keadaan g(2 – k) = 4k.
Penyelesaian:
(a)
g(x)=x3x−2=x3x−x=2 2x=2 x=1
(b)
g(x)=3x−2g(2−k)=4k3(2−k)−2=4k6−3k−2=4k −7k=−4 k=47
Diberi fungsi g : x → 3x – 2, cari
(a) nilai x apabila g(x) memeta kepada diri sendiri,
(b) nilai k dengan keadaan g(2 – k) = 4k.
Penyelesaian:
(a)
g(x)=x3x−2=x3x−x=2 2x=2 x=1
(b)
g(x)=3x−2g(2−k)=4k3(2−k)−2=4k6−3k−2=4k −7k=−4 k=47
Soalan 15:
Diberi fungsi f : x → px + 1, g : x → 3x – 5 dan fg(x) = 3px + q.
Ungkapkan p dalam sebutan q.
Penyelesaian:
f(x)=px+1, g(x)=3x−5fg(x)=p(3x−5)+1 =3px−5p+1Diberi fg(x)=3px+q3px−5p+1=3px+q −5p+1=q −5p=q−1 5p=1−q p=1−q5
Diberi fungsi f : x → px + 1, g : x → 3x – 5 dan fg(x) = 3px + q.
Ungkapkan p dalam sebutan q.
Penyelesaian:
f(x)=px+1, g(x)=3x−5fg(x)=p(3x−5)+1 =3px−5p+1Diberi fg(x)=3px+q3px−5p+1=3px+q −5p+1=q −5p=q−1 5p=1−q p=1−q5

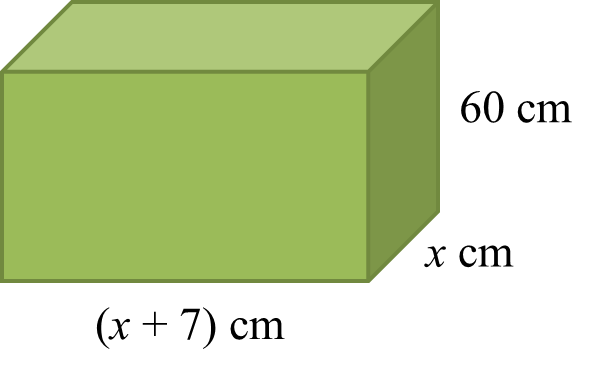
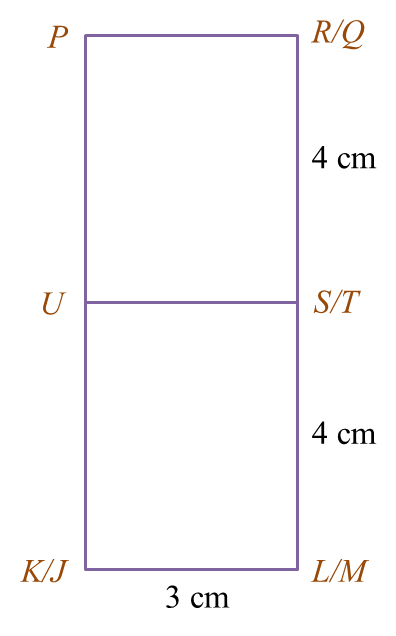
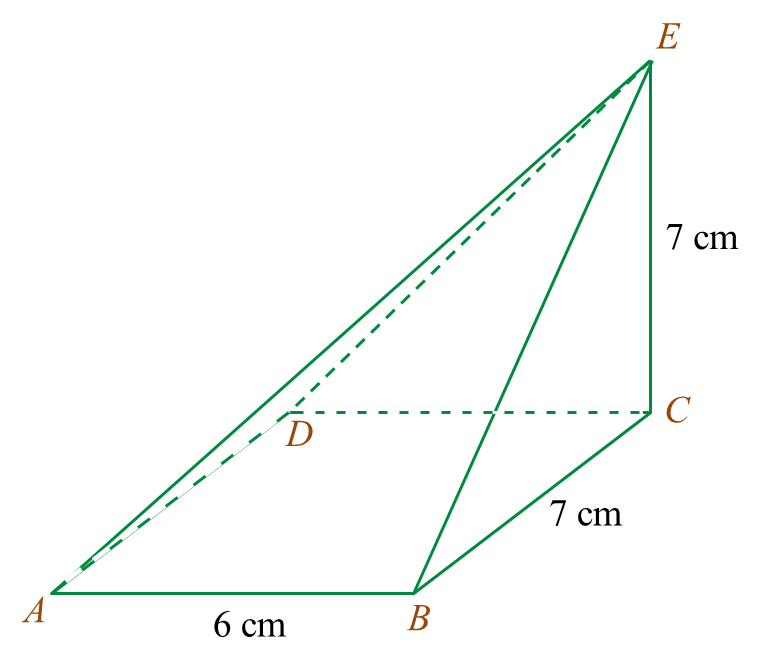 Rajah 7.1
Rajah 7.1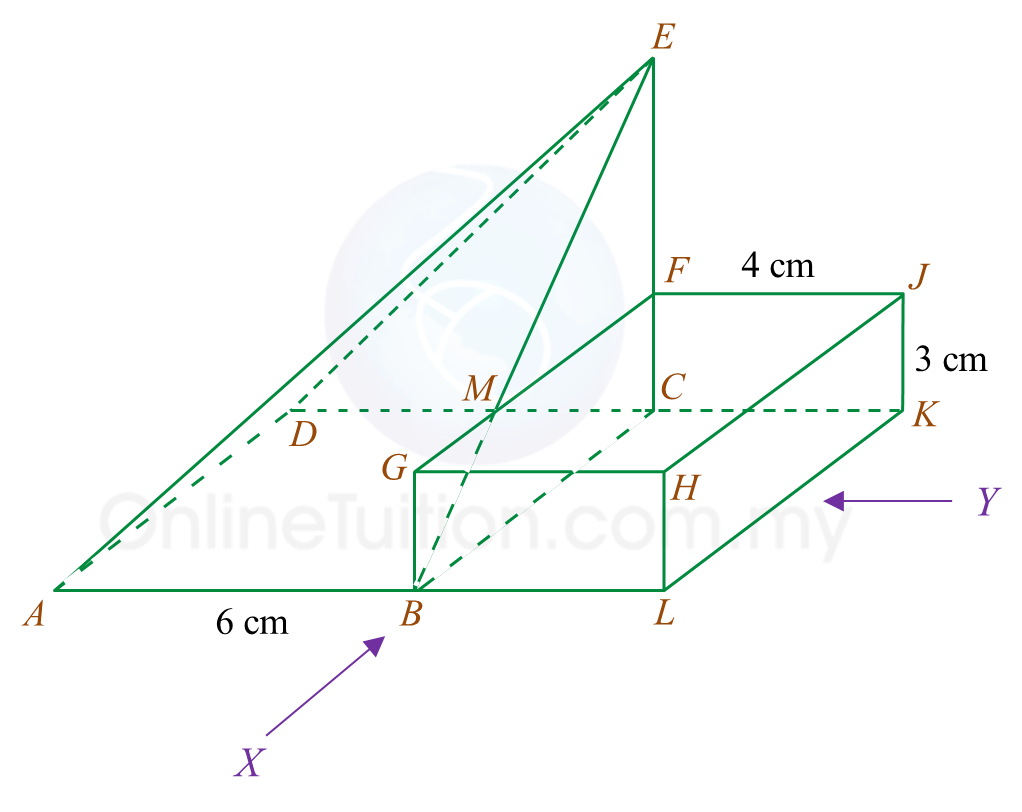 Rajah 7.2
Rajah 7.2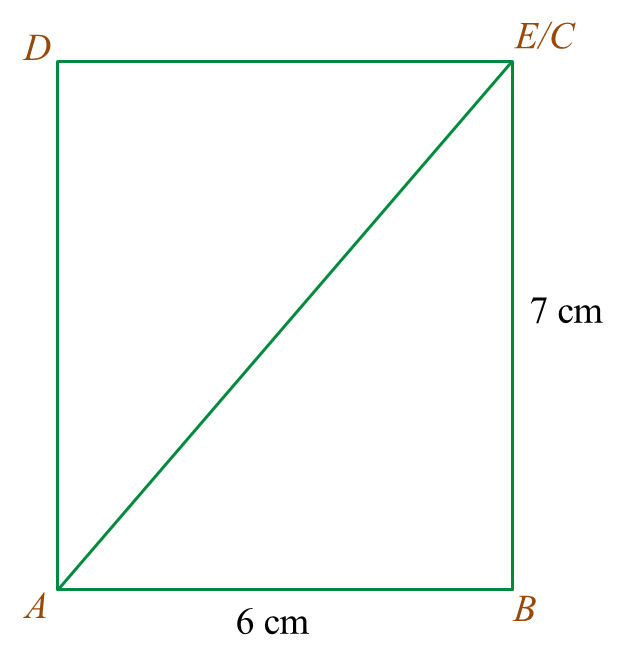
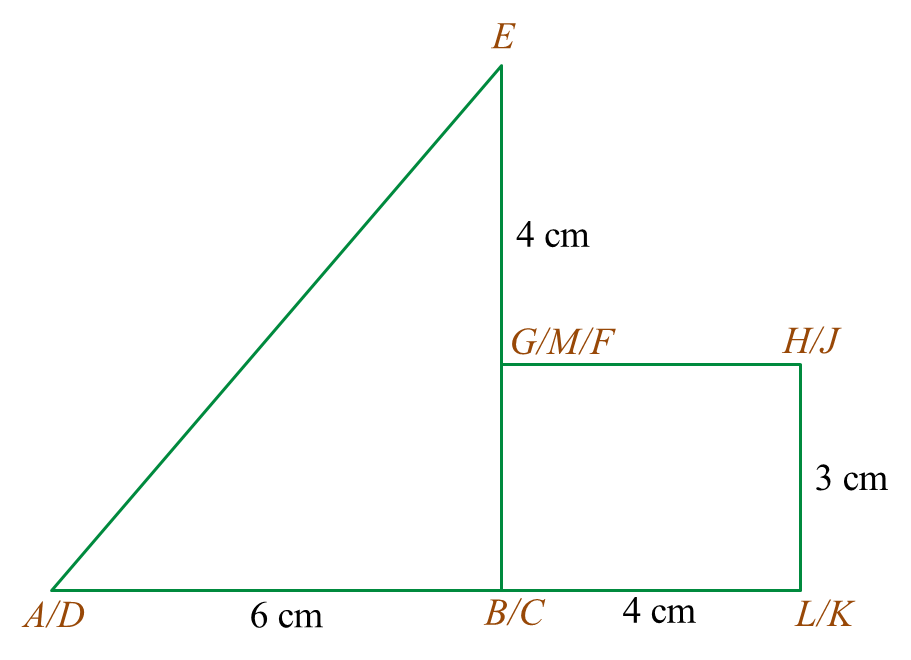
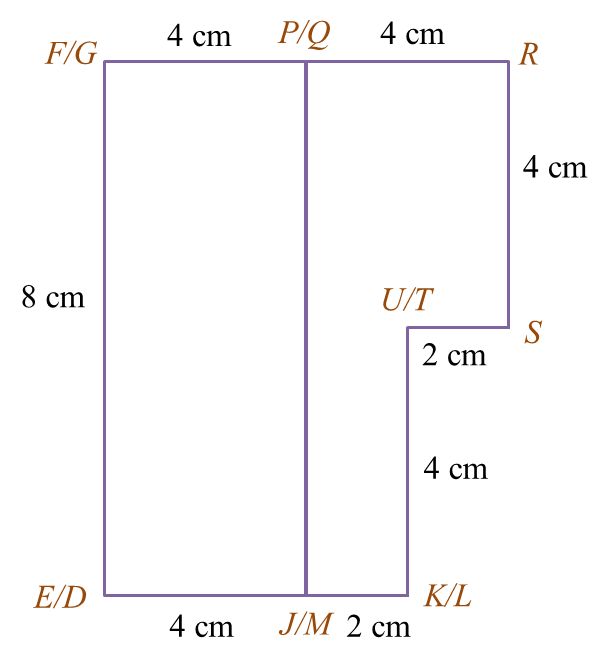
 Rajah 6.1
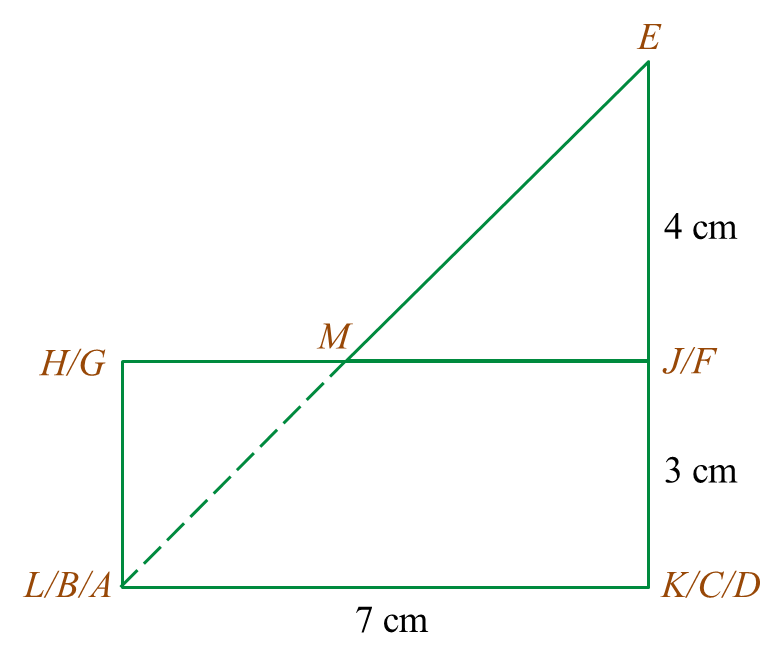
Rajah 6.1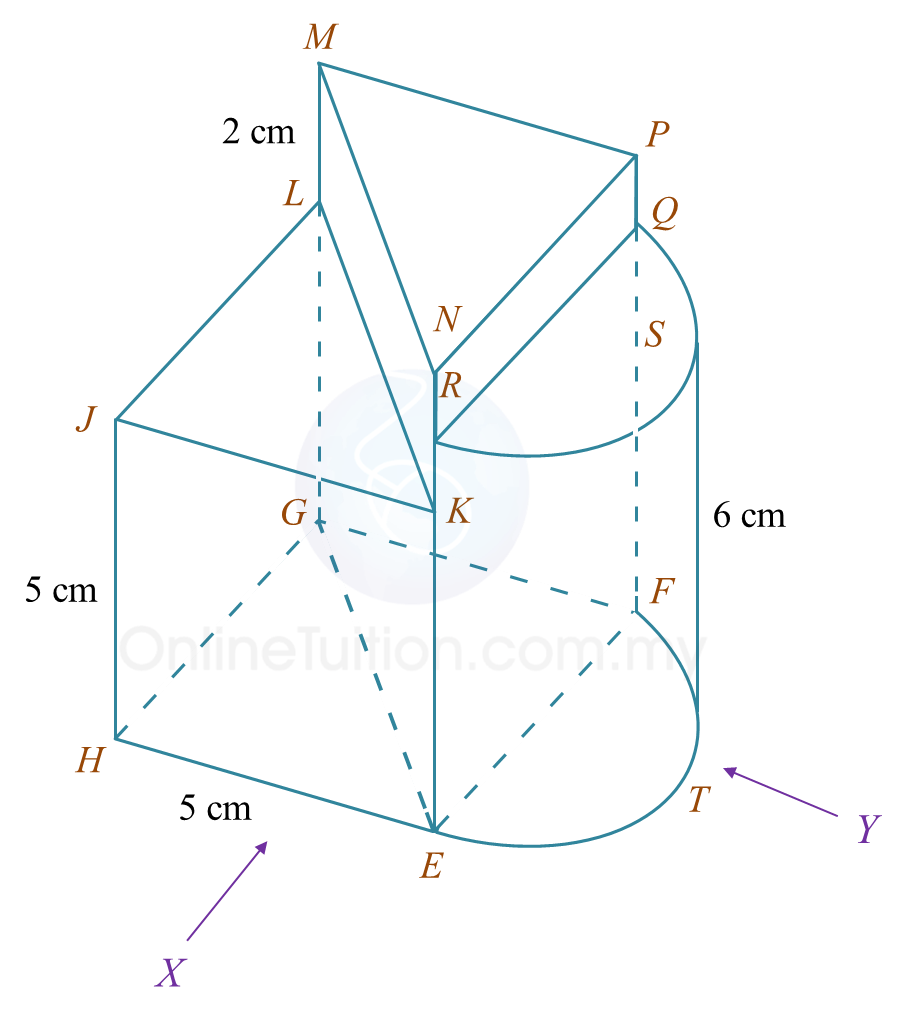 Rajah 6.2
Rajah 6.2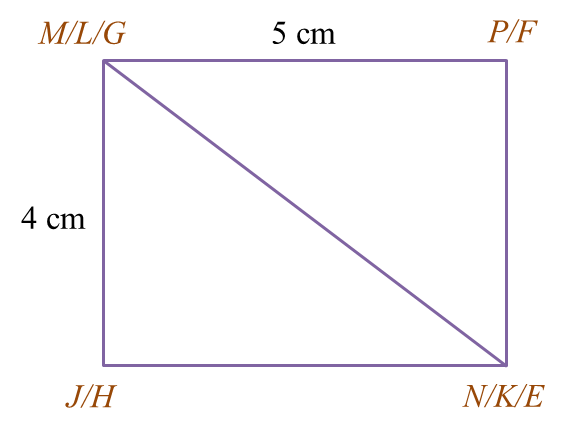
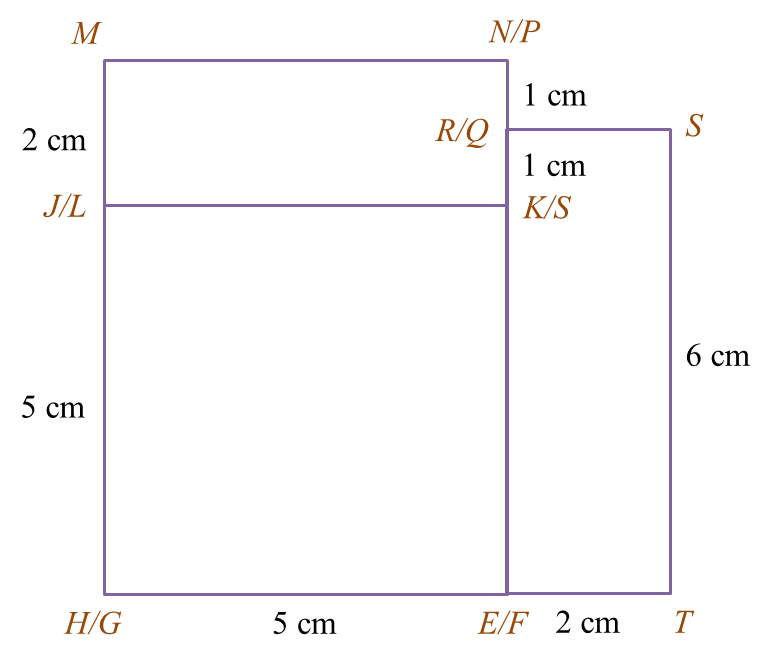
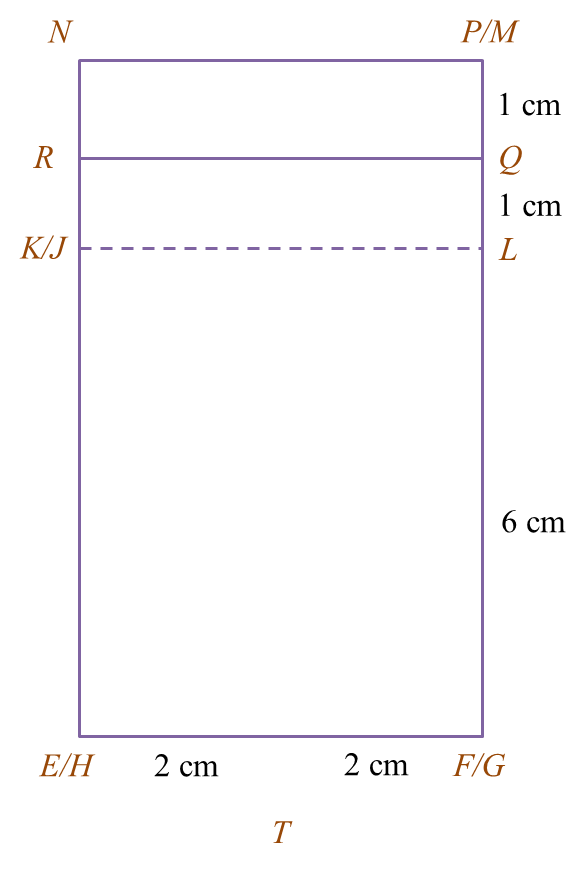
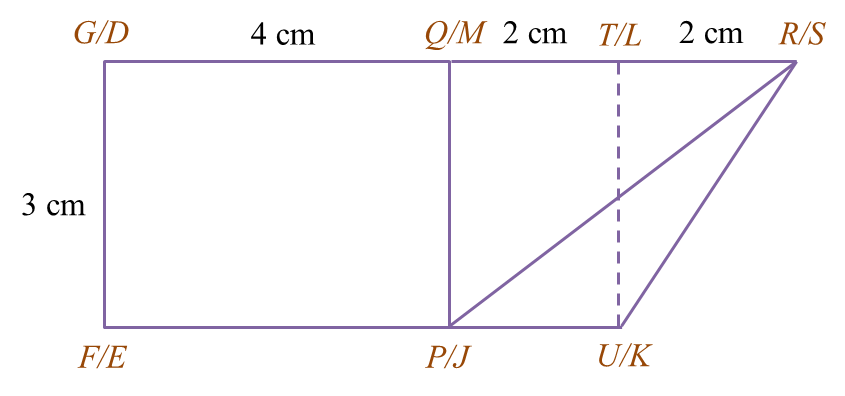
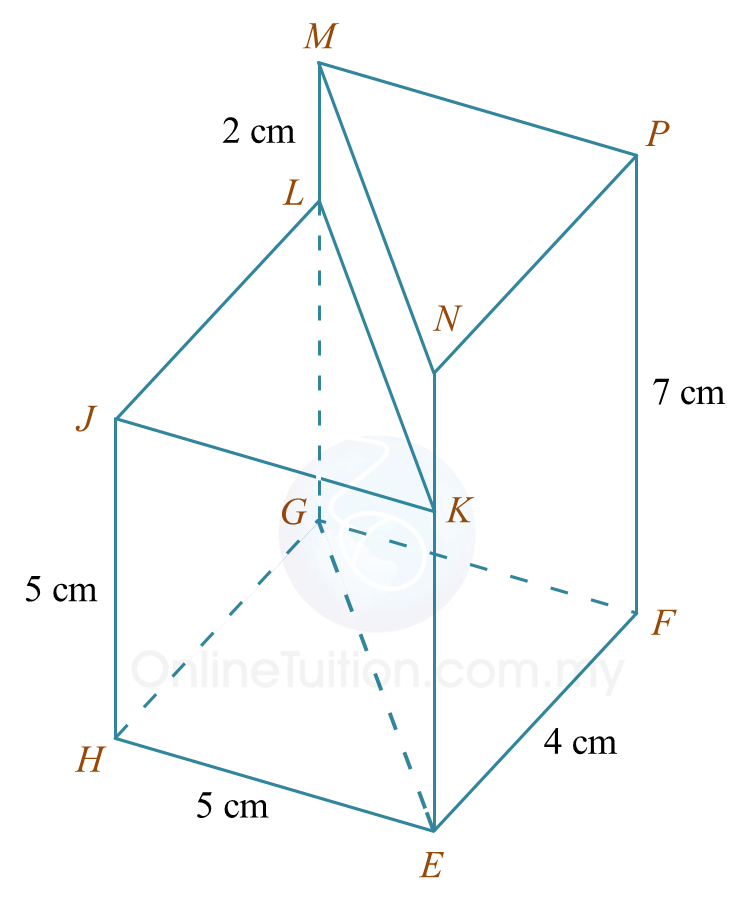
 Rajah 5.1
Rajah 5.1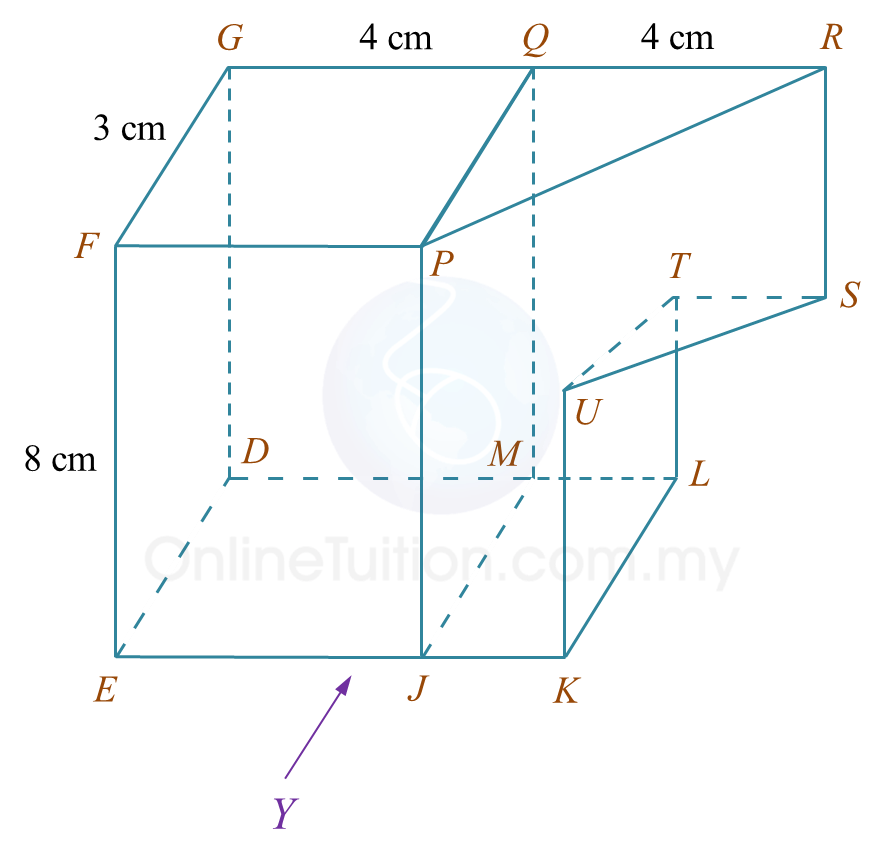 Rajah 5.2
Rajah 5.2