Soalan 10 (10 markah):
Rajah menunjukkan lengkung y = 2x2 – 18 dan garis lurus PQ yang merupakan tangen kepada lengkung itu pada titik K.
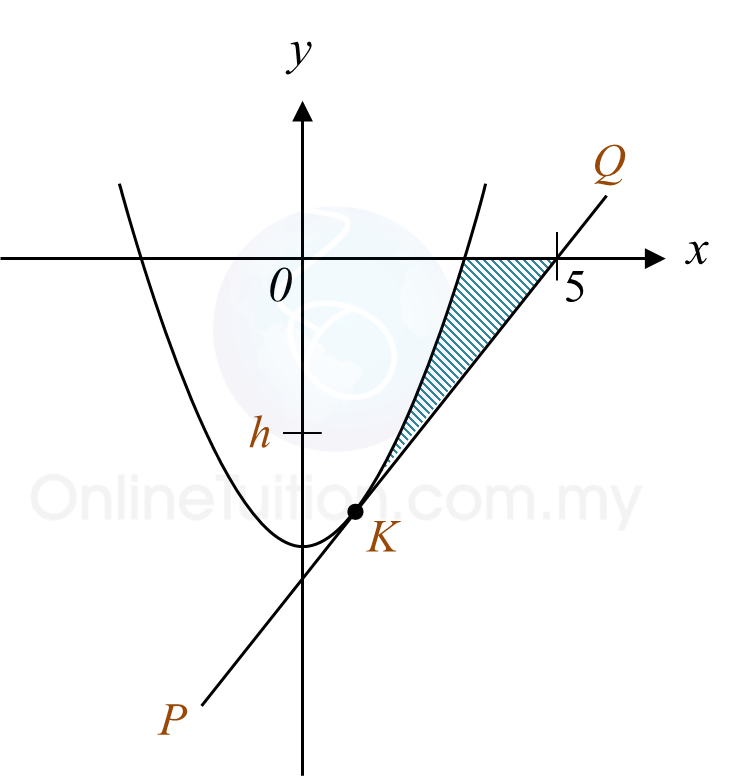
Diberi bahawa kecerunan garis lurus PQ ialah 4.
(a) Cari koordinat titik K
(b) Hitung luas rantau berlorek.
(c) Apabila rantau yang dibatasi oleh lengkung, paksi-x dan garis lurus y = h diputarkan melalui 180o pada paksi-y, isi padu kisaran ialah 65π unit3. Cari nilai h.
Penyelesaian:
(a)
y=2x2−18dydx=4xKecerunan garis lurus PQ=44x=4x=1Apabila x=1, y=2(1)2−18=−16Koordinat titik K=(1,−16).
(b)
Pada paksi-x, y=0∴2x2−18=02x2=18x2=9x=±3Lengkung itu memotong paksi-x di titik (−3,0) dan titik (3,0).Luas rantau berlorek= Luas Δ−Luas rantau yang dibatasi oleh lengkung=12(5−1)(16)−∫31ydx=32−∫31(2x2−18)dx=32−|[2x33−18x]31|=32−|(2(3)33−18(3))−(2(1)33−18(1))|=32−|(18−54−23+18)|=32−|−1823|=32−1823=1313 unit2
(c)
Isipadu kisaran=65ππ∫0hx2dy=65ππ∫0h(y2+9)dx=65π←y=2x2−18x2=y2+9[y24+9y]0h=650−(h24+9h)=65−h24−9h=65h2+36h+260=0(h+10)(h+26)=0h=−10 or h=−26 (ditolak)Maka, h=−10
Rajah menunjukkan lengkung y = 2x2 – 18 dan garis lurus PQ yang merupakan tangen kepada lengkung itu pada titik K.

Diberi bahawa kecerunan garis lurus PQ ialah 4.
(a) Cari koordinat titik K
(b) Hitung luas rantau berlorek.
(c) Apabila rantau yang dibatasi oleh lengkung, paksi-x dan garis lurus y = h diputarkan melalui 180o pada paksi-y, isi padu kisaran ialah 65π unit3. Cari nilai h.
Penyelesaian:
(a)
y=2x2−18dydx=4xKecerunan garis lurus PQ=44x=4x=1Apabila x=1, y=2(1)2−18=−16Koordinat titik K=(1,−16).
(b)
Pada paksi-x, y=0∴2x2−18=02x2=18x2=9x=±3Lengkung itu memotong paksi-x di titik (−3,0) dan titik (3,0).Luas rantau berlorek= Luas Δ−Luas rantau yang dibatasi oleh lengkung=12(5−1)(16)−∫31ydx=32−∫31(2x2−18)dx=32−|[2x33−18x]31|=32−|(2(3)33−18(3))−(2(1)33−18(1))|=32−|(18−54−23+18)|=32−|−1823|=32−1823=1313 unit2
(c)
Isipadu kisaran=65ππ∫0hx2dy=65ππ∫0h(y2+9)dx=65π←y=2x2−18x2=y2+9[y24+9y]0h=650−(h24+9h)=65−h24−9h=65h2+36h+260=0(h+10)(h+26)=0h=−10 or h=−26 (ditolak)Maka, h=−10