Question 6 (7 marks):
Diagram shows part of a rectangular wall painted with green, G, blue, B and purple, P subsequently.
The height of the wall is 2 m. The side length of the first coloured rectangle is 5 cm and the side length of each subsequent coloured rectangle increases by 3 cm.
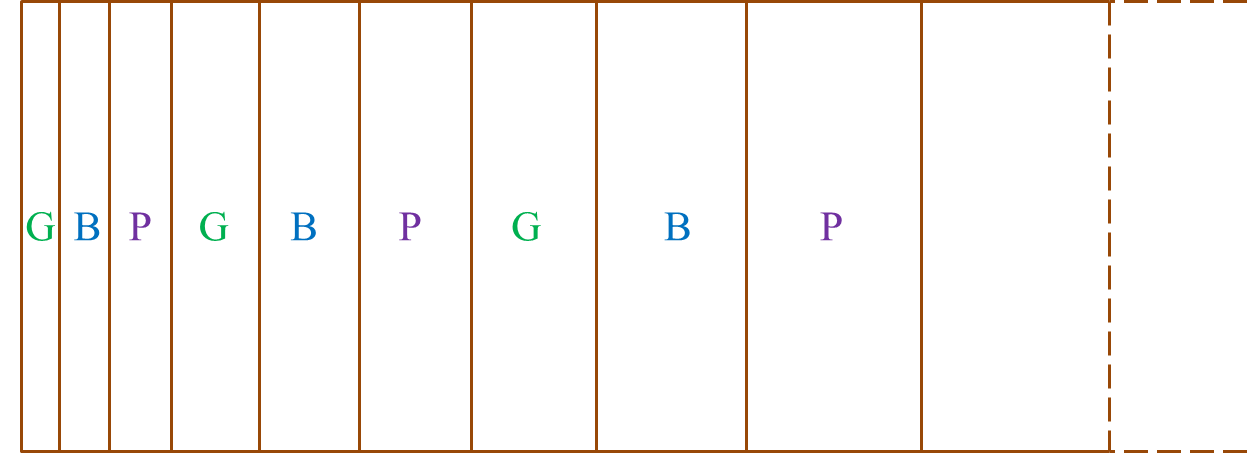
It is given that the total number of the coloured rectangles is 54.
(a) Find
(i) the side length, in cm, of the last coloured rectangle,
(ii) the total length, in cm, of the painted wall.
(b) Which coloured rectangle has an area of 28000 cm2?
Hence, state the colour of that particular rectangle.
Solution:
(a)
5, 8, 11, …
a = 5, d = 3
(i)
T54 = 1 + (54 – 1)d
= 5 + 53(3)
=164 cm
(ii)
Sn=n2(a+l)S54=542(5+164) =4563 cm
(b)
Area of the first rectangle
= 2 m × 5 cm
= 200 × 5
= 1000 cm
Area of the second rectangle
= 200 × (5 + 3)
= 1600 cm
Area of the third rectangle
= 200 × (5 + 3 + 3)
= 2200 cm
1000, 1600, 2200, …
a = 1000, d = 600
Tn = 28 000
a + (n – 1)d = 28 000
1000 + (n – 1)600 = 28 000
600(n – 1) = 27 000
n – 1 = 45
n = 46
The colour of that particular rectangle is green.
Diagram shows part of a rectangular wall painted with green, G, blue, B and purple, P subsequently.
The height of the wall is 2 m. The side length of the first coloured rectangle is 5 cm and the side length of each subsequent coloured rectangle increases by 3 cm.
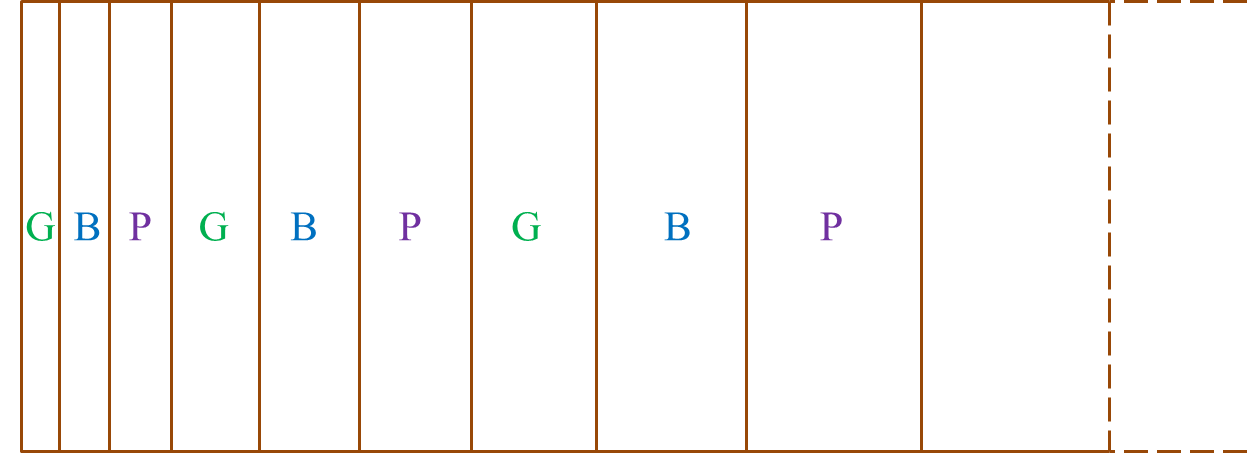
It is given that the total number of the coloured rectangles is 54.
(a) Find
(i) the side length, in cm, of the last coloured rectangle,
(ii) the total length, in cm, of the painted wall.
(b) Which coloured rectangle has an area of 28000 cm2?
Hence, state the colour of that particular rectangle.
Solution:
(a)
5, 8, 11, …
a = 5, d = 3
(i)
T54 = 1 + (54 – 1)d
= 5 + 53(3)
=164 cm
(ii)
Sn=n2(a+l)S54=542(5+164) =4563 cm
(b)
Area of the first rectangle
= 2 m × 5 cm
= 200 × 5
= 1000 cm
Area of the second rectangle
= 200 × (5 + 3)
= 1600 cm
Area of the third rectangle
= 200 × (5 + 3 + 3)
= 2200 cm
1000, 1600, 2200, …
a = 1000, d = 600
Tn = 28 000
a + (n – 1)d = 28 000
1000 + (n – 1)600 = 28 000
600(n – 1) = 27 000
n – 1 = 45
n = 46
The colour of that particular rectangle is green.
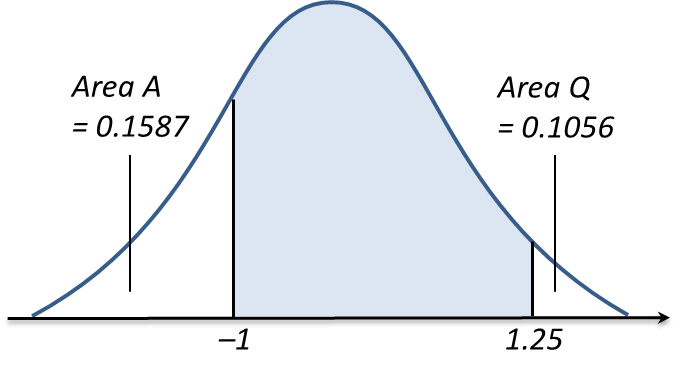
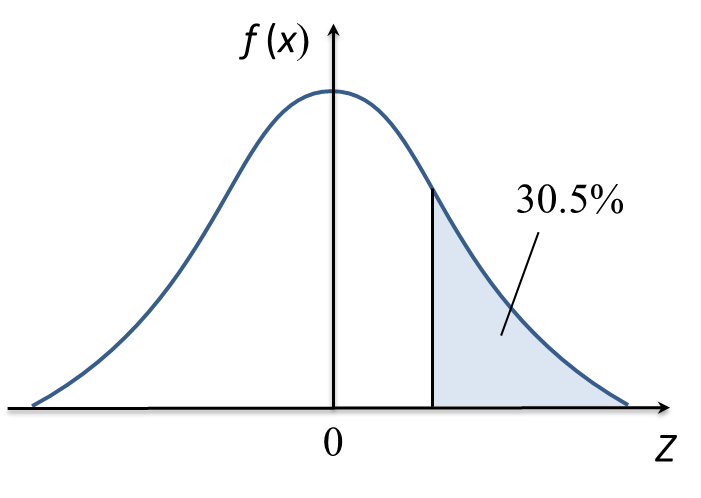 It is given the mean is 950 cm3 and the variance is 256 cm6. If the percentage of the volume more than V is 30.5%, find
It is given the mean is 950 cm3 and the variance is 256 cm6. If the percentage of the volume more than V is 30.5%, find
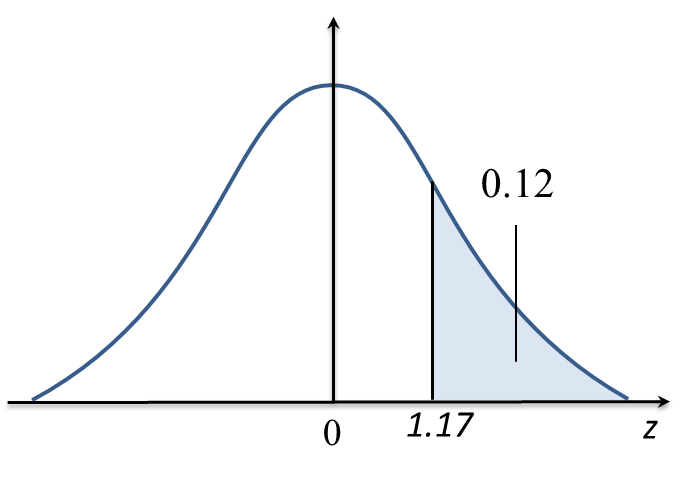 Thus, the minimum mark to obtain grade A is 66.
Thus, the minimum mark to obtain grade A is 66.