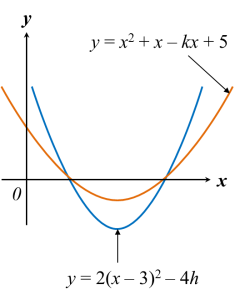
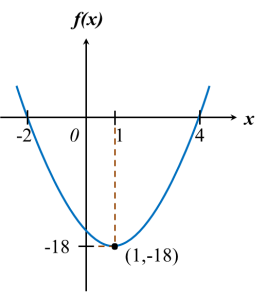
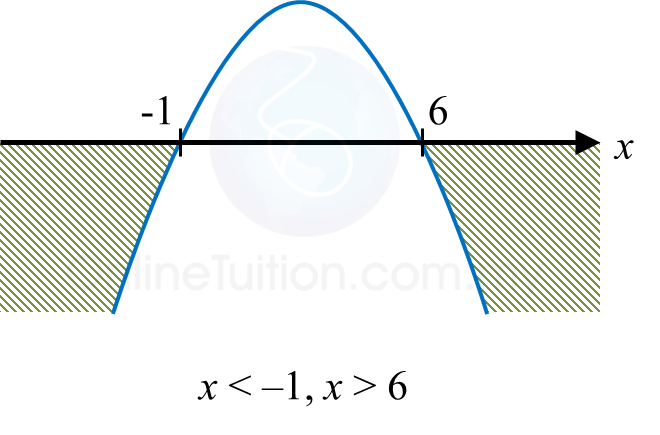
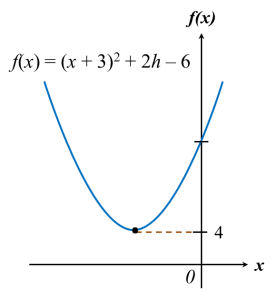
8.5.5 Sukatan Membulat, SPM Praktis (Kertas 2)

Posted on May 13, 2020 by Myhometuition

Soalan 5:
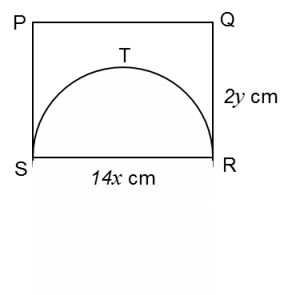
Rajah di bawah menunjukkan sebuah semi bulatan PTS, dengan pusat O dan jejari 8 cm. PTR ialah sector sebuah bulatan dengan pusat P dan Q ialah titik tengah OS.

[Guna π = 3.142]
Hitung
(a) ∠TOQ, dalam radians,
(b) panjang, dalam cm , lengkok TR,
(c) luas, dalam cm², kawasan berlorek.

Penyelesaian:
(a)

$\begin{array}{l} k o s ∠ T O Q = \frac{4}{8} = \frac{1}{2} \\ ∠ T O Q = 60^{o} \\ = 60 \times \frac{π}{180} \\ = 1.047 radians \end{array}$

(b)

$\begin{array}{l} ∠ T P O = 30^{o} \\ = 30 \times \frac{π}{180} \\ = 0.5237 \\ P T^{2} = 8^{2} + 8^{2} - 2 (8) (8) k o s 120 \\ P T^{2} = 192 \\ P T = \sqrt{192} \\ P T = 13.86 cm \\ Panjang lengkok T R = 13.86 \times 0.5237 \\ = 7.258 cm \end{array}$

(c)

$\begin{array}{l} Luas sektor P T R \\ = \frac{1}{2} \times {13.86}^{2} \times 0.5237 \\ = 50.30 {cm}^{2} \\ Panjang T Q \\ = \sqrt{P T^{2} - P Q^{2}} \\ = \sqrt{{13.86}^{2} - 12^{2}} \\ = 6.935 cm \\ Luas △ P T Q \\ = \frac{1}{2} \times 12 \times 6.935 \\ = 41.61 {cm}^{2} \\ Luas kawasan berlorek \\ = 50.30 - 41.61 \\ = 8.69 {cm}^{2} \end{array}$

7.3.4 Statistik, SPM Praktis (Kertas 1)

Posted on May 13, 2020 by Myhometuition

Soalan 7:
Satu set data mengandungi dua belas nombor positif.

$Diberi bahawa Σ {(x - \bar{x})}^{2} = 600 dan Σ x^{2} = 1032.$
Cari
(a) varians
(b) min

Penyelesaian:
(a)

$\begin{array}{l} Varians = \frac{Σ {(x - \bar{x})}^{2}}{N} \\ = \frac{600}{12} \\ = 50 \end{array}$

(b)

$\begin{array}{l} Varians = \frac{Σ x^{2}}{N} - {(\bar{x})}^{2} \\ 50 = \frac{1032}{12} - {(\bar{x})}^{2} \\ {(\bar{x})}^{2} = 86 - 50 \\ = 36 \\ \bar{x} = 36 \end{array}$

Soalan 8 (2 markah):
Jadual menunjukkan maklumat tentang suatu set data.

Jadual

Nyatakan
(a) nilai p jika m = 20,
(b) nilai q jika p = 2.5.

Penyelesaian:
(a)
Sisihan piawai baharu = sisihan piawai asal × p
20 = 5 × p
p = 4

(b)
Median baharu = [median asal × p] + 1
q = 2p × 1
q = 2(2.5) + 1
q = 5 + 1
q = 6

Soalan 9 (3 markah):
Jadual menunjukkan taburan skor yang diperolehi sekumpulan murid dalam suatu pertandingan.

Jadual

(a) Nyatakan nilai minimum bagi x jika skor mod ialah 4.
(b) Cari min skor bagi taburan itu jika x = 1.

Penyelesaian:
(a)
Nilai minimum bagi x = 8

(b)

$\begin{array}{l} Min \\ = \frac{1 (3) + 2 (6) + 3 (7) + 4 (1) + 5 (1)}{3 + 6 + 7 + 1 + 1} \\ = \frac{45}{18} \\ = 2.5 \end{array}$

7.3.3 Statistik, SPM Praktis (Kertas 1)

Posted on May 13, 2020 by Myhometuition

Soalan 5:
Satu set data terdiri daripada 9, 2, 7, x² – 1 dan 4. Diberi min ialah 6, cari
(a) nilai positif bagi x,
(b) median dengan menggunakan nilai x di (a).

Penyelesaian:
(a)

$\begin{array}{l} Min = 6 \\ \frac{9 + 2 + 7 + x^{2} - 1 + 4}{5} = 6 \\ x^{2} + 21 = 30 \\ x^{2} = 9 \\ x = \pm 3 \\ Nilai positif bagi x = 3. \end{array}$

(b)
Mengatur nombor dalam susunan menaik
2, 4, 7, 8, 9
Median = 7

Soalan 6:
Suatu set mempunyai tujuh nombor dengan sisihan piawai 3 dan suatu set lain mempunyai tiga nombor dengan sisihan piawai 4. Kedua-dua set nombor itu mempunyai min yang sama.
Jika dua set nombor tersebut digabungkan, cari varians.

Penyelesaian:

$\begin{array}{l} {\bar{X}}_{1} = \frac{Σ X_{1}}{n_{1}} \\ m = \frac{Σ X_{1}}{7} \\ Σ X_{1} = 7 m \\ m = \frac{Σ X_{2}}{3} \\ Σ X_{2} = 3 m \\ σ = \sqrt{\frac{Σ X^{2}}{N} - {(\bar{X})}^{2}} \\ σ^{2} = \frac{Σ X^{2}}{N} - {(\bar{X})}^{2} \\ 9 = \frac{Σ X_{1}^{2}}{7} - m^{2} \\ 63 = Σ X_{1}^{2} - 7 m^{2} \\ Σ X_{1}^{2} = 7 m^{2} + 63 \end{array}$

$\begin{array}{l} 16 = \frac{Σ X_{2}^{2}}{3} - m^{2} \\ 48 = Σ X_{2}^{2} - 3 m^{2} \\ Σ X_{2}^{2} = 48 + 3 m^{2} \\ Σ Y^{2} = Σ X_{1}^{2} + Σ X_{2}^{2} \\ Σ Y^{2} = 7 m^{2} + 63 + 3 m^{2} + 48 \\ = 10 m^{2} + 111 \\ Σ Y = Σ X_{1} + Σ X_{2} \\ Σ Y = 7 m + 3 m = 10 m \\ Varians Gabungan: \\ σ^{2} = \frac{Σ Y^{2}}{N} - {(\frac{Σ Y}{N})}^{2} \\ σ^{2} = \frac{10 m^{2} + 111}{10} - {(\frac{10 m}{10})}^{2} \\ = \frac{10 m^{2} + 111}{10} - m^{2} \\ = \frac{10 m^{2} + 111 - 10 m^{2}}{10} \\ = \frac{111}{10} = 11.1 \end{array}$

6.8.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Posted on May 13, 2020 by Myhometuition

Soalan 8:
Rajah di bawah menunjukkan sisi empat ABCD. Titik C terletak pada paksi-y.

Persamaan garis lurus AD ialah 2y = 5x – 21.
(a) Cari
(i) persamaan garis lurus AB,
(ii) koordinat A,
(b) Titik P bergerak dengan keadaan jaraknya dari titik D sentiasa 5 unit.
Cari persamaan lokus P.

Penyelesaian:

(a)(i)

$\begin{array}{l} 2 y = 5 x - 21 \\ y = \frac{5}{2} x - \frac{21}{2} \\ m_{A D} = \frac{5}{2} \\ m_{A B} \times m_{A D} = - 1 \\ m_{A B} \times \frac{5}{2} = - 1 \\ m_{A B} = - \frac{2}{5} \\ Persamaan A B \\ y - y_{1} = m_{A B} (x - x_{1}) \\ y + 1 = - \frac{2}{5} (x + 2) \\ 5 y + 5 = - 2 x - 4 \\ 5 y = - 2 x - 9 \end{array}$

(a)(ii)

$\begin{array}{l} 2 y = 5 x - 21 .......... (1) \\ 5 y = - 2 x - 9 .......... (2) \\ (1) \times 5 : 10 y = 25 x - 105 .......... (3) \\ (2) \times 2 : 10 y = - 4 x - 18 .......... (4) \\ (2) - (4) : 0 = 29 x - 87 \\ x = 3 \\ Dari (1), \\ 2 y = 15 - 21 \\ 2 y = - 6 \\ y = - 3 \\ A = (3, - 3) \end{array}$

(b)

$\begin{array}{l} y = 2, \\ 4 = 5 x - 21 \\ 5 x = 25 \\ x = 5 \\ Titik D = (5, 2) \\ P D = 5 \\ \sqrt{{(x - 5)}^{2} + {(y - 2)}^{2}} = 5 \\ {(x - 5)}^{2} + {(y - 2)}^{2} = 25 \\ x^{2} - 10 x + 25 + (y^{2} - 4 y + 4) = 25 \\ x^{2} + y^{2} - 10 x - 4 y + 4 = 0 \end{array}$

6.8.7 Geometri Koordinat, SPM Praktis (Kertas 2)

Posted on May 13, 2020 by Myhometuition

6.8.7 Geometri Koordinat, SPM Praktis (Kertas 2)
Soalan 7:
Penyelesaian secara lukisan berskala tidak diterima.
Rajah di bawah menunjukkan segi tiga PRS. Sisi PR bersilang dengan paksi-y pada titik Q.

(a) Diberi PQ : QR = 2 : 3, cari
(i) koordinat P,
(ii) persamaan garis lurus PS,
(iii) luas, dalam unit², segi tiga PRS.
(b) Titik M bergerak dengan keadaan jaraknya dari titik R adalah sentiasa dua kali jaraknya dari titik S.
Cari persamaan lokus M.

Penyelesaian:

(a)(i)

$\begin{array}{l} P = (\frac{2 (6) + 3 h}{2 + 3}, \frac{2 (12) + 3 k}{2 + 3}) \\ (0, 6) = (\frac{12 + 3 h}{5}, \frac{24 + 3 k}{5}) \\ \frac{12 + 3 h}{5} = 0 \\ 3 h = - 12 \\ h = - 4 \\ \frac{24 + 3 k}{5} = 6 \\ 3 k = 30 - 24 \\ k = 2 \\ P = (- 4, 2) \end{array}$

(a)(ii)

$\begin{array}{l} m_{P S} = \frac{2 - (- 6)}{- 4 - 2} \\ = - \frac{8}{6} \\ = - \frac{4}{3} \\ Persamaan P S : \\ y - y_{1} = - \frac{4}{3} (x - 2) \\ y - (- 6) = - \frac{4}{3} x + \frac{8}{3} \\ 3 y + 18 = - 4 x + 8 \\ 3 y = - 4 x - 10 \end{array}$

(a)(iii)

$\begin{array}{l} Luas △ P R S \\ = \frac{1}{2} | \begin{array}{l} - 4 2 6 \\ 2 - 612 \end{array} \begin{array}{l} - 4 \\ 2 \end{array} | \\ = \frac{1}{2} | (24 + 24 + 12) - (4 - 36 - 48) | \\ = \frac{1}{2} | 60 - (- 80) | \\ = 70 {unit}^{2} \end{array}$

(b)

$\begin{array}{l} Katakan P = (x, y) \\ M R = 2 M S \\ \sqrt{{(x - 6)}^{2} + {(y - 12)}^{2}} = 2 \sqrt{{(x - 2)}^{2} + {(y + 6)}^{2}} \\ {(x - 6)}^{2} + {(y - 12)}^{2} = 4 [{(x - 2)}^{2} + {(y + 6)}^{2}] \\ x^{2} - 12 x + 36 + y^{2} - 24 y + 144 = 4 [x^{2} - 4 x + 4 + y^{2} + 12 y + 36] \\ x^{2} - 12 x + y^{2} - 24 y + 180 = 4 x^{2} - 16 x + 4 y^{2} + 48 y + 160 \\ 3 x^{2} + 3 y^{2} - 4 x + 72 y - 20 = 0 \end{array}$

4.2.4 SPM Praktis, Persamaan Serentak

Posted on May 13, 2020 by Myhometuition

Soalan 7:
Diberi perimeter sebuah segi empat tepat ialah 24 cm dan luasnya ialah 35 cm² . Cari panjang dan lebar segi empat tepat itu.

Penyelesaian:
Anggap panjang = x cm dan lebar = y cm.
Diberi perimeter = 24 cm
Maka, 2x + 2y = 24
x + y = 12 ------ (1)

Diberi luas = 112 cm²
Maka, xy = 35 ------ (1)

Dari persamaan (1): y = 12 – x ------ (3)
Ganti (3) ke dalam (2):
x (12 – x) = 35
12x – x² = 35
x² – 12x + 35 = 0
(x – 5)(x – 7) = 0
x = 5, 7

Ganti x = 5 ke dalam (3):
y = 12 – 5 = 7

Ganti x = 7 ke dalam (3):
y = 12 – 7 = 5

Maka,
panjang = 5 cm dan lebar = 7 cm
atau
panjang = 7 cm dan lebar = 5 cm.

Soalan 8:

Dalam rajah di atas, PQRS ialah sekeping kertas berbentuk segi empat tepat dengan luas 112 cm² . STR berbentuk semibulatan digunting daripada kertas itu. Perimeter kertas yang tinggal ialah 52 cm. Dengan menggunakan π = 22/7, hitung nilai-nilai integer x dan y.

Penyelesaian:
Diberi luas PQRS = 112 cm²
Maka, (14x)(2y) = 112
28xy = 112
xy = 4 ------ (1)

Diberi perimeter kertas yang tinggal PSTRQ = 52 cm
PS + QR + PQ + Panjang lengkok STR = 52
2y + 2y + 14x + ½ (2πr) = 52
4y + 14x + (22/7) (7x) = 52
4y + 14x + 22x = 52
4y + 36x = 52
y + 9x = 13 ------ (2)

Dari persamaan (2): y = 13 – 9x ------ (3)

Ganti (3) ke dalam (1):
x (13 – 9x) = 4
13x – 9x² = 4
9x² – 13x + 4 = 0
(x – 1)(9x – 4) = 0
x = 1 atau 4/9 (bukan integer)

Dari (3):
Nilai integer x = 1,
Nilai integer y yang sepadan
= 13 – 9(1)
= 4.

3.7.4 Fungsi Kuadratik, SPM Praktis (Soalan Panjang)

Posted on May 13, 2020 by Myhometuition

Soalan 6:

Rajah di atas menunjukkan graf lengkung y = x² + x – kx + 5 dan y = 2(x – 3) – 4h yang bersilang pada dua titik pada paksi-x. Cari
(a) nilai k dan nilai h,
(b) nilai minimum bagi kedua-dua lengkung itu.

Penyelesaian:
(a)

$\begin{array}{l} y = x^{2} + x - k x + 5 \\ = x^{2} + (1 - k) x + 5 \\ = {[x + \frac{(1 - k)}{2}]}^{2} - {(\frac{1 - k}{2})}^{2} + 5 \\ paksi simetri bagi graf ini ialah \\ x = - \frac{(1 - k)}{2} \end{array}$

$\begin{array}{l} y = 2 {(x - 3)}^{2} - 4 h \\ paksi simetri bagi graf ini ialah \\ x = 3. \\ Maka, - \frac{1 - k}{2} = 3 \\ - 1 + k = 6 \\ k = 7 \end{array}$

$\begin{array}{l} Gantikan k = 7 ke dalam persamaan \\ y = x^{2} + x - 7 x + 5 \\ = x^{2} - 6 x + 5 \\ Pada paksi - x, y = 0; \\ x^{2} - 6 x + 5 = 0 \\ (x - 1) (x - 5) = 0 \\ x = 1, 5 \end{array}$

$\begin{array}{l} Pada titik (1, 0) \\ Gantikan x = 1, y = 0 ke dalam graf: \\ y = 2 {(x - 3)}^{2} - 4 h \\ 0 = 2 {(1 - 3)}^{2} - 4 h \\ 4 h = 2 (4) \\ 4 h = 8 \\ h = 2 \end{array}$

(b)

$\begin{array}{l} Lengkung y = x^{2} - 6 x + 5 \\ = {(x - 3)}^{2} - 9 + 5 \\ = {(x - 3)}^{2} - 4 \\ Maka, nilai minimumnya = - 4. \\ Bagi lengkung y = 2 {(x - 3)}^{2} - 8, nilai minimum = - 8. \end{array}$

3.7.3 Fungsi Kuadratik, SPM Praktis (Soalan Panjang)

Posted on May 13, 2020 by Myhometuition

Soalan 5:
Diberi fungsi kuadratik f(x) = 2x² – px + p mempunyai nilai minimum –18 pada nilai x = 1.

Cari nilai p dan nilai q.
Dengan nilai p dan nilai q yang diperoleh, cari nilai-nilai x di mana graf f(x), memotong paksi-x.
Seterusnya, lakarkan graf bagi f(x).

Penyelesaian:
(a)

$\begin{array}{l} f (x) = 2 x^{2} - p x + q \\ = 2 [x^{2} - \frac{p}{2} x + \frac{q}{2}] \\ = 2 [{(x + \frac{- p}{4})}^{2} - {(\frac{- p}{4})}^{2} + \frac{q}{2}] \\ = 2 [{(x - \frac{p}{4})}^{2} - \frac{p^{2}}{16} + \frac{q}{2}] \\ = 2 {(x - \frac{p}{4})}^{2} - \frac{p^{2}}{2} + q \end{array}$

$\begin{array}{l} Maka, \frac{p}{4} = 1 - - - - - - (1) \\ dan - \frac{p^{2}}{8} + q = - 18 - - - (2) \\ Dari (1), p = 4. \\ Ganti p = 4 ke dalam (2) : \\ - \frac{{(4)}^{2}}{8} + q = - 18 \\ - \frac{16}{8} + q = - 18 \\ q = - 18 + 2 \\ = - 16 \end{array}$

(b)

$\begin{array}{l} f (x) = 2 x^{2} - 4 x - 16 \\ Memotong paksi- x, f (x) = 0. \\ 2 x^{2} - 4 x - 16 = 0 \\ x^{2} - 2 x - 8 = 0 \\ (x - 4) (x + 2) = 0 \\ x = 4, - 2 \\ Graf f (x) memotong paksi- x di x = - 2 dan x = 4. \end{array}$

(c)

3.6.4 Fungsi Kuadratik, SPM Praktis (Soalan Pendek)

Posted on May 13, 2020 by Myhometuition

Soalan 7:
Cari julat nilai k jika persamaan kuadratik 3(x² – kx – 1) = k – k² mempunyai dua punca nyata yang berbeza.

Penyelesaian:

$\begin{array}{l} 3 (x^{2} - k x - 1) = k - k^{2} \\ 3 x^{2} - 3 k x - 3 - k + k^{2} = 0 \\ 3 x^{2} - 3 k x + k^{2} - k - 3 = 0 \\ a = 3, b = - 3 k, c = k^{2} - k - 3 \\ Dua punca nyata berbeza . \\ b^{2} - 4 a c > 0 \\ {(- 3 k)}^{2} - 4 (3) (k^{2} - k - 3) > 0 \\ 9 k^{2} - 12 k^{2} + 12 k + 36 > 0 \\ - 3 k^{2} + 12 k + 36 > 0 \\ - k^{2} + 4 k + 12 > 0 \\ k^{2} - 4 k - 12 < 0 \\ (k + 2) (k - 6) < 0 \\ k = - 2, 6 \end{array}$

$Julat nilai k ialah - 2 < k < 6.$

Soalan 8 (4 markah):
Fungsi kuadratik f ditakrifkan oleh f(x) = x² + 4x + h, dengan keadaan h ialah pemalar.
(a) Ungkapkan f(x) dalam bentuk (x + m)² + n, dengan keadaan m dan n ialah pemalar.

(b) Diberi nilai minimum bagi f(x) ialah 8, cari nilai h.

Penyelesaian:
(a)
f(x) = x² + 4x + h
= x² + 4x + (2)²– (2)²+ h
= (x + 2)² – 4 + h

(b)
Diberi nilai minimum bagi f(x) = 8
– 4 + h = 8
h = 12

Soalan 9 (3 markah):
Cari julat nilai x dengan keadaan fungsi kuadratik f(x) = 6 + 5x – x² ialah negatif.

Penyelesaian:
(a)
f(x) < 0
6 + 5x – x²< 0
(6 – x)(x + 1) < 0
x < –1, x > 6

3.6.2 Fungsi Kuadratik, SPM Praktis (Soalan Pendek)

Posted on May 13, 2020 by Myhometuition

Soalan 5:
Diberi persamaan kuadratik hx² – (h + 2)x – (h – 4) = 0 mempunyai punca-punca yang nyata dan berbeza. Cari julat nilai h.

Penyelesaian:

$\begin{array}{l} Persamaan kuadratik h x^{2} - (h + 2) x - (h - 4) = 0 \\ mempunyai punca-punca yang nyata dan berbeza . \\ Maka, b^{2} - 4 a c > 0 \\ {(- h - 2)}^{2} - 4 (h) (- h + 4) > 0 \\ h^{2} + 4 h + 4 + 4 h^{2} - 16 h > 0 \\ 5 h^{2} - 12 h + 4 > 0 \\ (5 h - 2) (h - 2) > 0 \\ Pekali h^{2} positif, graf melengkung ke bawah \\ (5 h - 2) (h - 2) = 0 \\ h = \frac{2}{5}, 2 \end{array}$

$\begin{array}{l} Julat nilai h bagi (5 h - 2) (h - 2) >0 ialah \\ h < \frac{2}{5} atau h > 2. \end{array}$

Soalan 6:
Rajah di bawah menunjukkan graf fungsi kuadratik f(x) = (x + 3)² + 2h – 6, dengan keadaan h ialah pemalar.

(a) Nyatakan persamaan paksi simetri bagi lengkung itu.
(b) Diberi nilai minimum bagi fungsi itu ialah 4, cari nilai h.

Penyelesaian:
(a)
Apabila x + 3 = 0
x = –3
Maka, persamaan paksi simetri bagi lengkung itu ialah x = –3.

(b)
Apabila x + 3 = 0, f(x) = 2h – 6
Nilai minimum bagi f(x) ialah 2h – 6.
Maka, 2h – 6 = 4
2h = 10
h = 5