Soalan 3:
Garis lurus y = 5x – 1 tidak bersilang dengan lengkung y = 2x2 + x + h. Carikan julat nilai h.
Penyelesaian:
y=5x−1 ...... (1)y=2x2+x+h ...... (2)Gantikan (1) ke dalam (2),5x−1=2x2+x+h2x2+x+h−5x+1=02x2−4x+h+1=0 b2−4ac<0(−4)2−4(2)(h+1)<0 16−8h−8<0 8<8h h>1
Garis lurus y = 5x – 1 tidak bersilang dengan lengkung y = 2x2 + x + h. Carikan julat nilai h.
Penyelesaian:
y=5x−1 ...... (1)y=2x2+x+h ...... (2)Gantikan (1) ke dalam (2),5x−1=2x2+x+h2x2+x+h−5x+1=02x2−4x+h+1=0 b2−4ac<0(−4)2−4(2)(h+1)<0 16−8h−8<0 8<8h h>1
Soalan 4:
Cari nilai maksimum bagi fungsi 5 – x – 2x2 , dan nilai x apabila ini berlaku.
Penyelesaian:
5−x−2x2=−2x2−x+5=−2[x2+12x−52]=−2[x2+12x+(14)2−(14)2−52]=−2[(x+14)2−116−52]=−2[(x+14)2−4116]=−2(x+14)2+518
Nilai 5−x−2x2 adalah maksimum apabila2(x+14)2=0 x=−14Nilai maksimum bagi 5−x−2x2 ialah 518.
Cari nilai maksimum bagi fungsi 5 – x – 2x2 , dan nilai x apabila ini berlaku.
Penyelesaian:
5−x−2x2=−2x2−x+5=−2[x2+12x−52]=−2[x2+12x+(14)2−(14)2−52]=−2[(x+14)2−116−52]=−2[(x+14)2−4116]=−2(x+14)2+518
Nilai 5−x−2x2 adalah maksimum apabila2(x+14)2=0 x=−14Nilai maksimum bagi 5−x−2x2 ialah 518.

 Rajah
Rajah

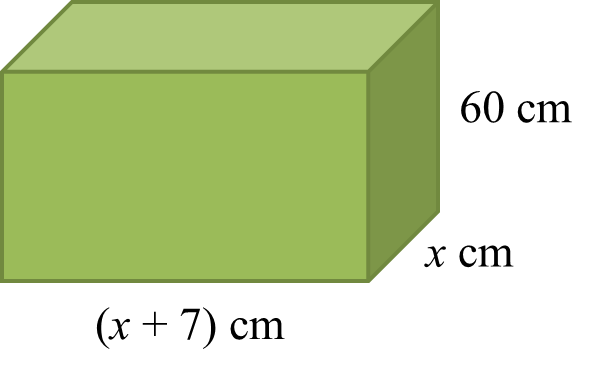
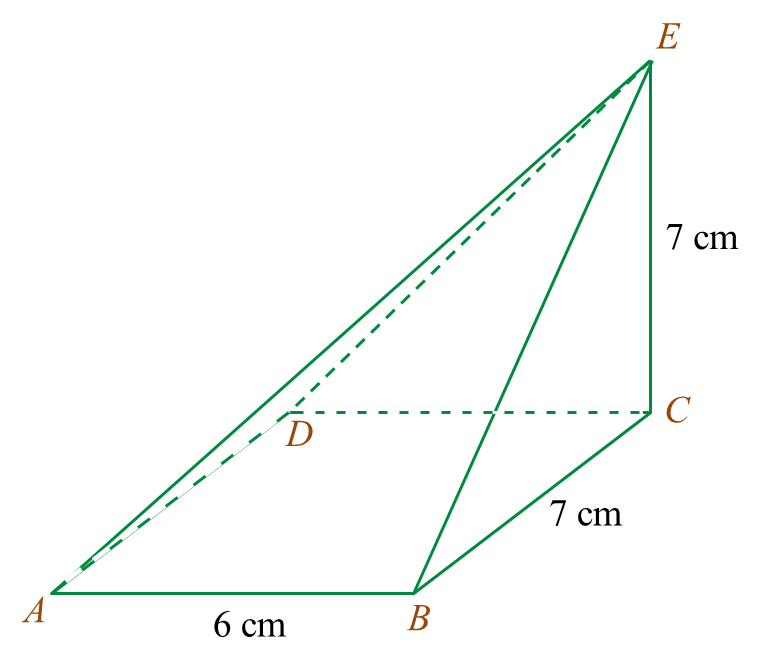 Rajah 7.1
Rajah 7.1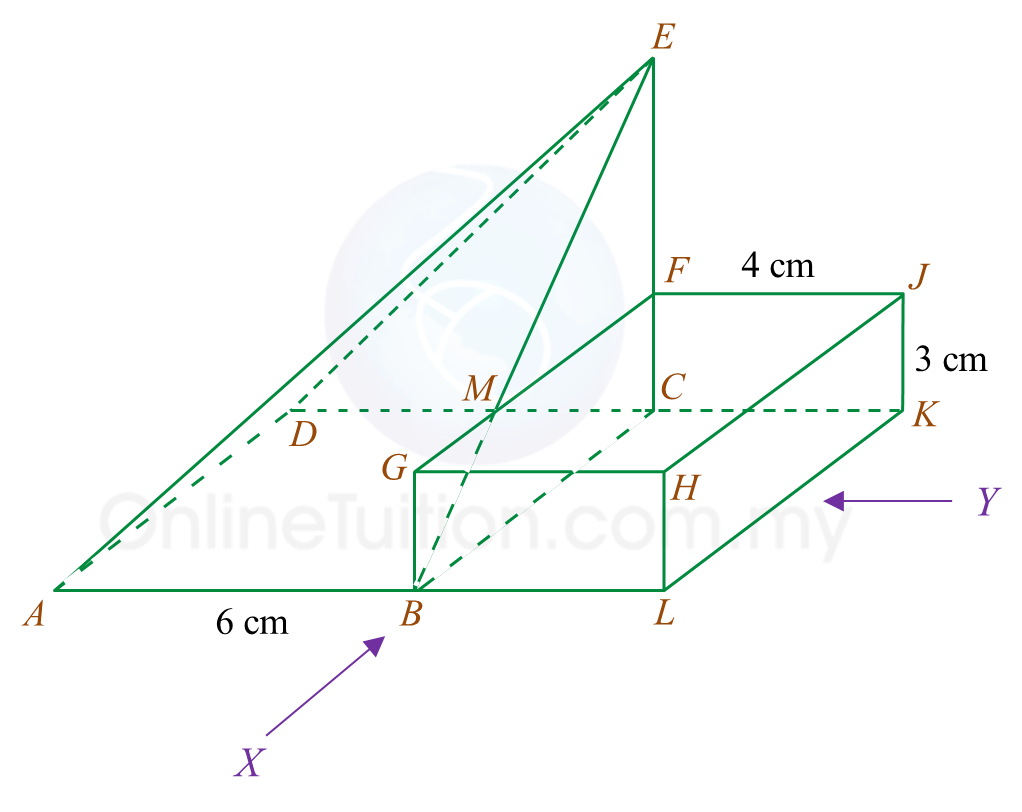 Rajah 7.2
Rajah 7.2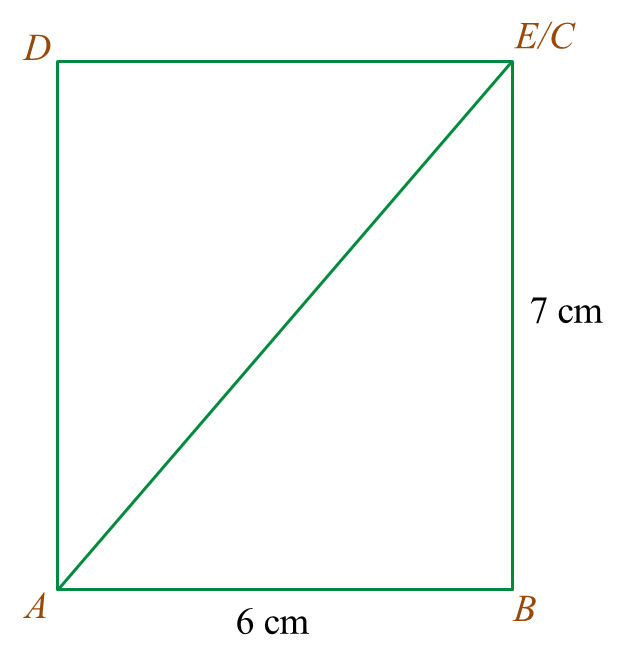
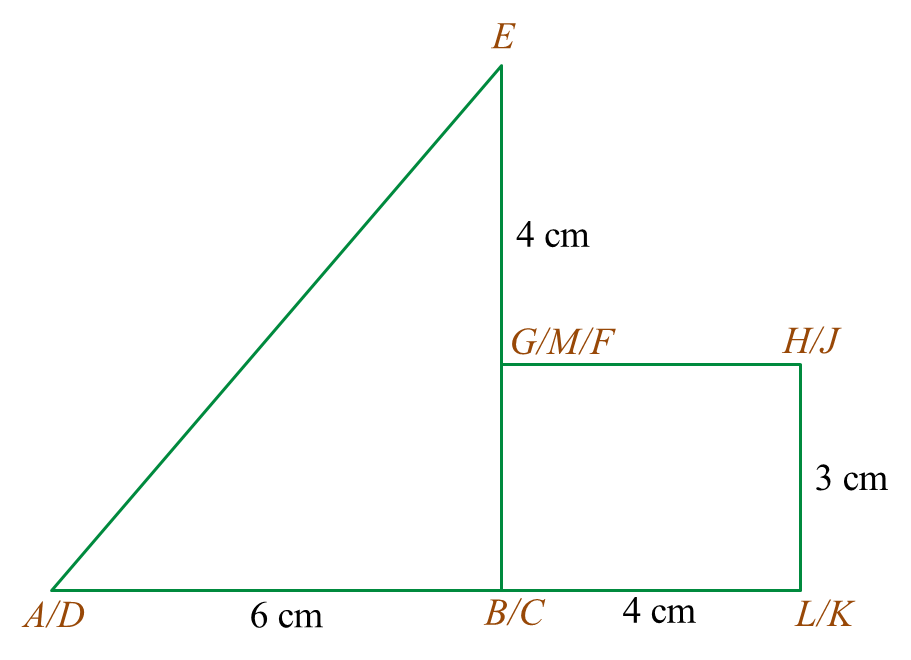
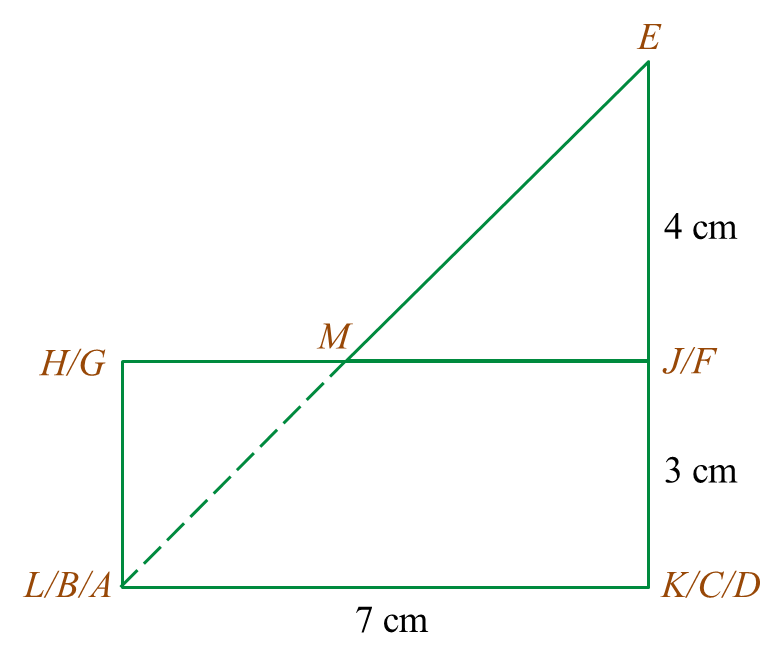
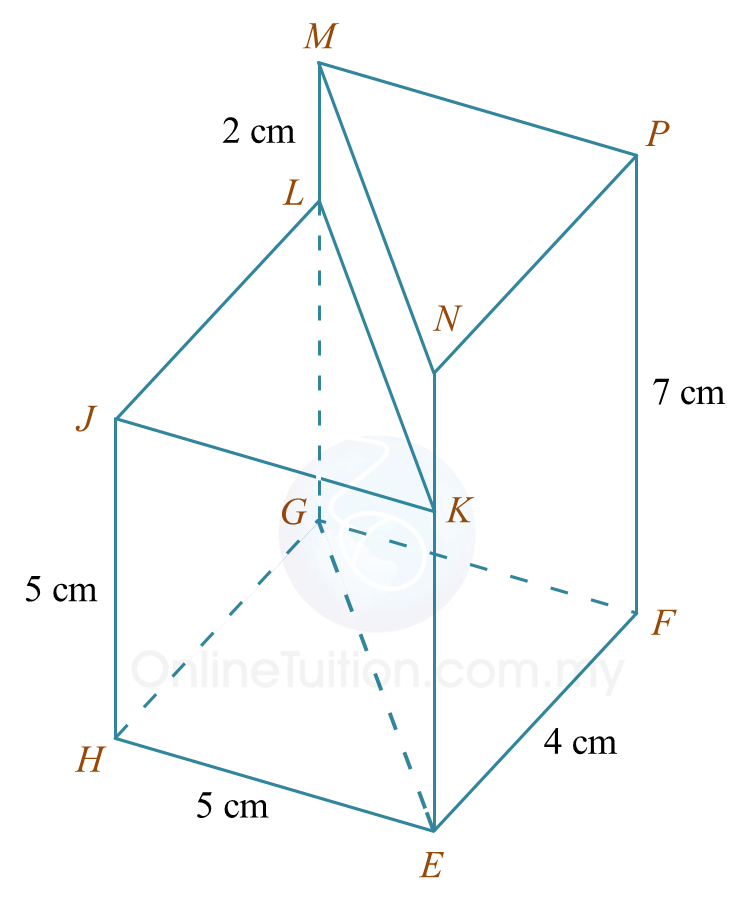 Rajah 6.1
Rajah 6.1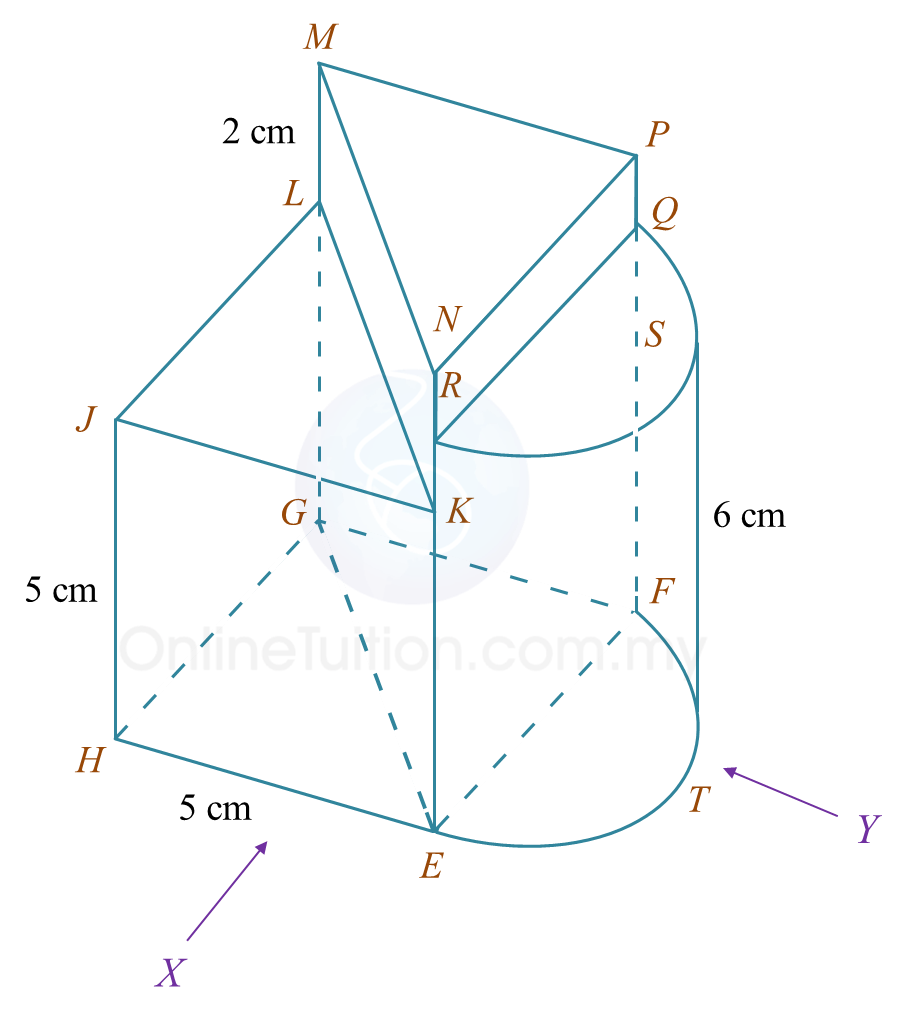 Rajah 6.2
Rajah 6.2