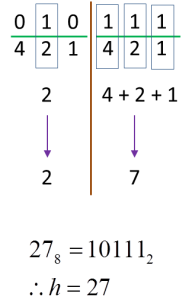
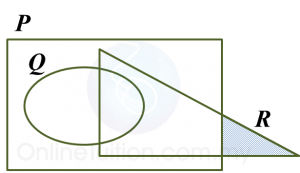
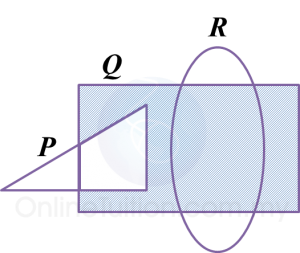
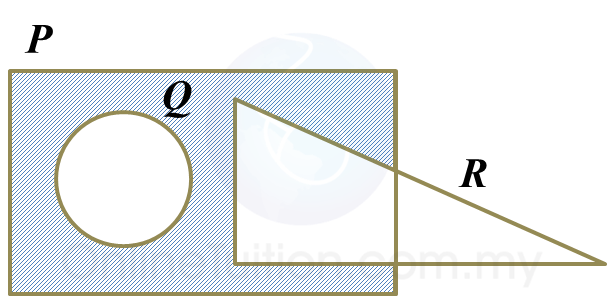
Soalan 11:
Ungkapkan setiap yang berikut sebagai nombor dalam asas dua.
(a) 26 + 24 + 1
(b) 25 + 23 + 2 + 20
Penyelesaian:
Ungkapkan setiap yang berikut sebagai nombor dalam asas dua.
(a) 26 + 24 + 1
(b) 25 + 23 + 2 + 20
Penyelesaian:
Soalan 12:
Nyatakan nilai digit 2 bagi nombor 324175 , dalam asas sepuluh.
Penyelesaian:
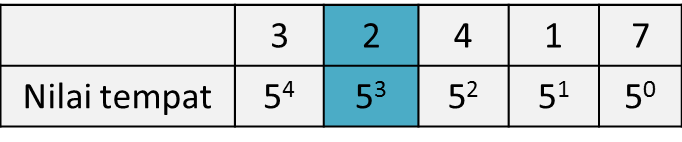
Nilai digit 2
= 2 × 53
= 250
Nyatakan nilai digit 2 bagi nombor 324175 , dalam asas sepuluh.
Penyelesaian:

Nilai digit 2
= 2 × 53
= 250
Soalan 13:
101102 + 1112 =
Penyelesaian:

Secara alternatif, mendapatkan jawapan terus daripada kalkulator saintifik.
101102 + 1112 =
Penyelesaian:

Secara alternatif, mendapatkan jawapan terus daripada kalkulator saintifik.
Soalan 14:
1100102 – 1112 =
Penyelesaian:
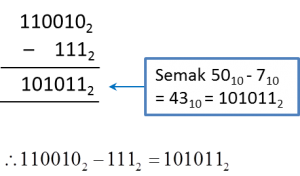
Secara alternatif, mendapatkan jawapan terus daripada kalkulator saintifik.
1100102 – 1112 =
Penyelesaian:

Secara alternatif, mendapatkan jawapan terus daripada kalkulator saintifik.