2.5.4 SPM Praktis (Soalan Panjang)

Posted on May 12, 2020 by Myhometuition

Soalan 13 (4 markah):
Rajah menunjukkan sebuah laluan taman berbentuk segi empat tepat. Terdapat 8 keping batu pemijak berbentuk bulat yang sama saiz dibina di laluan itu.

Diberi luas laluan itu ialah 32 m², cari diameter, dalam m, sekeping batu pemijak itu.

Penyelesaian:

\begin{array}{l} Diberi luas laluan = 32 m^{2} = 320000 {cm}^{2} \\ x (x + 4) = 320000 \\ x^{2} + 4 x - 320000 = 0 \\ a = 1, b = 4, c = - 320000 \\ x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ x = \frac{- 4 \pm \sqrt{4^{2} - 4 (1) (- 320000)}}{2 (1)} \\ x = \frac{- 4 \pm \sqrt{1280016}}{2} \\ x = \frac{- 4 + 1131.38}{2} atau \frac{- 4 - 1131.38}{2} \\ x = 563.69 atau - 567.69 (abaikan) \\ Diameter sekeping batu pemijak = x \\ = 563.69 cm \\ = 5.64 m \end{array}

Soalan 14 (5 markah):
Penyelesaian dengan kaedah matriks tidak dibenarkan untuk menjawap soalan ini.
Rajah menunjukkan sebuah basikal dan sebuah basikal roda tiga.

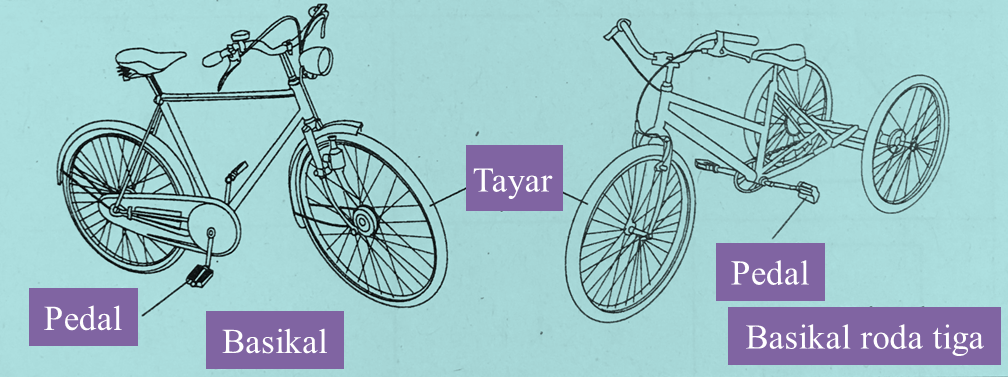
Hitung bilangan basikal dan bilangan basikal roda tiga jika terdapat 64 pedal dan 74 tayar.

Penyelesaian:
Katakan basikal = x dan basikal roda tiga = y
Jadi,
2x + 2y = 64 …………. (1)
2x + 3y = 74 …………. (2)
(2) – (1)
3y – 2y = 74 – 64
y = 10

Apabila y = 10
Dari (2)
2x + 3(10) = 74
2x = 74 – 30
2x = 44
x = 22

Maka, bilangan basikal ialah 22 dan bilangan basikal roda tiga ialah 10.

3.5.5 Set, SPM Practis (Soalan Panjang)

Posted on May 12, 2020 by Myhometuition

Soalan 9 (3 markah):
(a) Diberi bahawa set E = {nombor kuasa dua sempurna} dan set F = {9, 16, 25}.
Lengkapkan gambar rajah Venn di ruang jawapan untuk menunjukkan hubungan antara set E dan set F.

Jawapan:

(b) Gambar rajah Venn pada Rajah 1 menunjukkan set X, set Y dan set Z.
Set semesta, ξ = X U Y U Z.

Nyatakan hubungan yang diwakili oleh rantau berlorek di antara set X, set Y dan set Z.

Penyelesaian:
(a)

(b)

Maka, hubungan yang diwakili oleh rantau berlorek di antara set X, set Y dan set Z ialah (X ∩ Y) ∪ Z

Soalan 10 (3 markah):
Gambar rajah Venn di ruang jawapan menunjukkan set P, set Q dan set R dengan keadaan set semesta ξ = P U Q U R.
Pada rajah di ruang jawapan, lorek set
(a) P’,
(b) (P ∩ Q) U R

Jawapan:

Penyelesaian:
(a)

(b)

9.6.5 Bumi Sebagai Sfera, SPM Praktis (Kertas 2)

Posted on May 12, 2020 by Myhometuition

Soalan 6:
Rajah di bawah menunjukkan titik-titik P, Q, R, A, K dan C, pada permukaan bumi. O ialah pusat bumi.

(a) Cari kedudukan bagi A.

(b) Diberi jarak QR ialah 3240 batu nautika, cari longitud bagi Q.

(c) Hitung jarak, dalam batu nautika, KA, diukur sepanjang selarian latitud sepunya.

(d) Sebuah kapal terbang berlepas dari A dan terbang arah barat ke K, sepanjang selarian latitud sepunya. Kemudian, ia terbang arah selatan ke Q. Purata laju kapal terbang itu ialah 550 knot.
Hitung jumlah masa, dalam jam, yang diambil bagi keseluruhan penerbangan itu.

Penyelesaian:

(a)
Longitud bagi A = (180^o – 15^o) = 165^o T
Latitud bagi A = 50^o U
Oleh itu, kedudukan bagi A = (50^o U, 165^o T).

(b)

\begin{array}{l} ∠ Q O R = \frac{3240}{60} \\ = 54^{o} \\ ∴ Longitud bagi Q = (165^{o} - 54^{o}) T \\ = 111^{o} T \end{array}

(c)
Jarak bagi KA
= 54 x 60 x kos 50^o= 2082.6 batu nautika

(d)

\begin{array}{l} Jumlah jarak = A K + K Q \\ = 2082.6 + (50 \times 60) \\ = 5082.6 batu nautika \\ Jumlah masa = \frac{5082.6}{550} \\ = 9.241 jam \end{array}

9.6.4 Bumi Sebagai Sfera, SPM Praktis (Kertas 2)

Posted on May 12, 2020 by Myhometuition

Soalan 4:
P (25^o U, 35^o T), Q (25^o U, 40^o B), R dan S adalah empat titik yang terletak pada permukaan bumi. PS ialah diameter selarian latitud sepunya 25^o U.

(a) Cari longitud S.

(b) R terletak 3300 batu nautika di selatan P diukur sepanjang permukaan bumi.
Hitung latitud R.

(c) Hitung jarak terpendek, dalam batu nautika, dari P ke S diukur sepanjang permukaan bumi.

(d) Sebuah kapal terbang berlepas dari R dan terbang arah utara ke P dan kemudian terbang arah barat ke Q. Jumlah masa yang diambil bagi keseluruhan penerbangan itu ialah 12 jam 24 minit.
(i) Hitung jarak, dalam batu nautika, dari P arah barat ke Q diukur sepanjang selarian latitud sepunya.
(ii) Hitung purata laju, dalam knot, bagi keseluruhan penerbangan itu.

Penyelesaian:
(a)
Longitud S = (180^o – 35^o) B = 145^o B

(b)

\begin{array}{l} ∠ P O R = \frac{3300}{60} \\ = 55^{o} \\ Latitud R = {(55 - 25)}^{o} \\ = 30^{o} S \end{array}

(c)
Jarak terpendek dari P ke S
= (65 + 65) x 60
= 130 x 60
= 7800 batu nautika

(d)(i)
Jarak PQ
= (35 + 40) x 60 x kos 25^o= 75 x 60 x kos 25^o= 4078.4 batu nautika

\begin{array}{l} (ii) \\ Jumlah jarak dilalui \\ R P + P Q \\ = 3300 + 4078.4 \\ = 7378.4 batu nautika \\ Laju purata = \frac{Jumlah jarak dilalui}{Masa diambil} \\ = \frac{7378.4}{12.4} \leftarrow 12 jam 24 min = 12 + \frac{12}{60} = 12 + 0.4 \\ = 595.0 knot \end{array}

Soalan 5:
A (53^o U, 84^o B), K (53^o U, 25^o B), C dan D adalah empat titik yang terletak pada permukaan bumi. AC ialah diameter selarian latitud 53^o U.

(a) Nyatakan kedudukan bagi C.

(b) Hitung jarak terpendek, dalam batu nautika, dari A ke C diukur sepanjang permukaan bumi.

(c) Hitung jarak, dalam batu nautika, dari A arah timur ke K diukur sepanjang selarian latitud sepunya.

(d) Sebuah kapal terbang berlepas dari K arah ke selatan ke D. Purata laju penerbangan itu ialah 420 knot dan masa yang diambil untuk penerbangan itu ialah 6½ jam.
Hitung
(i) jarak, dalam batu nautika, dari K ke D diukur sepanjang meridian.
(ii) latitud bagi D.

Penyelesaian:
(a)
Latitud bagi C = 53^o U
Longitud bagi C = (180^o – 84^o) T = 96^o T
Oleh itu, kedudukan bagi C = (53^o U, 96^o T)

(b)
Jarak terpendek dari A ke C
= (180 – 53 – 53) x 60
= 74 x 60
= 4440 batu nautika

(c)
Jarak dari A ke K
= (84 – 25) x 60 x kos 53^o= 59 x 60 x kos 53^o= 2130.43 batu nautika

(d)

\begin{array}{l} (i) \\ Jarak dilalui dari K ke D \\ = 420 \times 6 \frac{1}{2} \leftarrow \begin{array}{l} Jarak dilalui \\ = purata laju \times masa diambil \end{array} \\ = 2730 batu nautika \\ (ii) \\ Perbezaan latitud antara K ke D \\ = \frac{2730}{60} \\ = {45.5}^{o} \\ ∴ Latitud bagi D = (53^{o} - {45.5}^{o}) U \\ = {7.5}^{o} U \end{array}

9.6.3 Bumi Sebagai Sfera, SPM Praktis (Kertas 2)

Posted on May 11, 2020 by Myhometuition

Soalan 3:
Rajah di bawah menunjukkan titik A (34^o S, 40^o B) dan B (34^o S, 80^o T) yang terletak pada permukaan bumi. AC ialah diameter selarian latitud sepunya 34^o S.

(a) Nyatakan longitud bagi C.

(b) Hitung jarak, dalam batu nautika, dari A arah timur ke B, diukur sepanjang selarian latitud sepunya 34^o S.

(c) K terletak ke utara ke A dan jarak terpendek dari A ke K diukur sepanjang permukaan bumi ialah 4440 batu nautika.
Hitung latitud bagi K.

(d) Sebuah kapal terbang berlepas dari B dan terbang arah barat ke A sepanjang selarian latitud sepunya. Kemudian, kapal terbang itu terbang arah utara ke K. Purata laju bagi keseluruhan penerbangan itu ialah 450 knot.
Hitung jumlah masa, dalam jam, bagi keseluruhan penerbangan itu.

Penyelesaian:
(a)
Longitud bagi C = (180^o – 40^o) T = 140^o T

(b)
Jarak bagi AB
= (40 + 80) x 60 x kos 34^o= 120 x 60 x kos 34^o= 5969 batu nautika

(c)

\begin{array}{l} ∠ A O K = \frac{4440}{60} \\ = 74^{o} \\ Latitud bagi K = {(74 - 34)}^{o} U \\ = 40^{o} U \end{array}

(d)

\begin{array}{l} Jumlah jarak dilalui \\ B A + A K \\ = 5969 + 4440 \\ = 10409 batu nautika \\ Jumlah masa diambil = \frac{Jumlah jarak dilalui}{Purata laju} \\ = \frac{10409}{450} \\ = 23.13 jam \end{array}

7.5.4 Kebarangkalian II, SPM Praktis (Kertas 2)

Posted on May 11, 2020 by Myhometuition

Soalan 7:
Rajah bawah menunjukkan 4 keping kad berlabel dengan huruf.

Dua keping kad dipilih secara rawak daripada kotak itu, satu demi satu, tanpa dikembalikan.
(a) Senaraikan ruang sampel.
(b) Carikan kebarangkalian bahawa
(i) sekurung-kurungnya satu kad yang dipilih berlabel C,
(ii) kedua-dua kad yang dipilih berlabel dengan huruf yang sama.

Penyelesaian:
(a)
Ruang sampel, S
= {(C, O₁), (C, O₂), (C, L), (O₁, C), (O₁, O₂), (O₁, L), (O₂, C), (O₂, O₁), (O₂, L), (L, C), (L, O₁), (L, O₂)}
n(S) = 12

(b)(i)
Sekurung-kurungnya satu kad yang dipilih berlabel C
= {(C, O₁), (C, O₂), (C, L), (O₁, C), (O₂, C), (L, C)}

Kebarangkalian = \frac{6}{12} = \frac{1}{2}

(b)(ii)
Kedua-dua kad yang dipilih berlabel dengan huruf yang sama
= {(O₁, O₂), (O₂, O₁)}

Kebarangkalian = \frac{2}{12} = \frac{1}{6}

Soalan 8 (5 markah):
Jadual di bawah menunjukkan beberapa ahli Persatuan Bulan Sabit Merah dan Persatuan St John Ambulans yang telah ditugaskan untuk satu tugasan luar di beberapa tempat sempena Hari Bendera.

Dua ahli daripada persatuan itu telah diturunkan secara rawak di beberapa tempat tersebut.

(a) Senaraikan semua kesudahan yang mungkin dalam ruang sampel ini.
Anda juga boleh menggunakan huruf seperti A untuk Amy dan seterusnya.

(b) Dengan menyenaraikan semua kesudahan yang mungkin, cari kebarangkalian bahawa
(i) seorang budak lelaki dan seorang budak perempuan telah diturunkan di suatu tempat.
(ii) kedua-dua ahli yang telah diturunkan di suatu tempat adalah daripada persatuan yang sama.

Penyelesaian:
(a)
S = {(A, J), (A, N), (A, F), (A, C), (A, M), (J, A), (J, N), (J, F), (J, C), (J, M), (N, A), (N, J), (N, F), (N, C), (N, M), (F, A), (F, J), (F, N), (F, C), (F, M), (C, A), (C, J), (C, N), (C, F), (C, M),(M, A), (M, J), (M, N), (M, F), (M, C)}

(b)(i)
{(A, F), (A, C), (A, M), (J, F), (J, C), (J, M), (N, F), (N, C), (N, M), (F, A), (F, J), (F, N), (C, A), (C, J), (C, N), (M, A), (M, J), (M, N)}

\begin{array}{l} Kebarangkalian \\ = \frac{18}{30} \\ = \frac{3}{5} \end{array}

(b)(ii)
{(A, F), (A, C), (F, A), (F, C), (C, A), (C, F), (J, N), (J, M), (N, J), (N, M), (M, J), (M, N)}

\begin{array}{l} Kebarangkalian \\ = \frac{12}{30} \\ = \frac{2}{5} \end{array}

7.5.3 Kebarangkalian II, SPM Praktis (Kertas 2)

Posted on May 11, 2020 by Myhometuition

Soalan 5:
Satu dadu yang adil dilambung. Kemudian sekeping kad dipilih secara rawak dari sebuah kotak yang mengandungi sekeping kad kuning, sekeping kad merah dan sekeping kad ungu.

(a) Dengan menggunakan huruf Y untuk mewakili kad kuning, huruf R untuk menwakili kad merah dan huruf P untuk mewakili kad ungu, lengkapkan ruang sampel pada ruang jawapan.

(b) Dengan menyenarai semua kesudahan yang mungkin bagi peristiwa itu, cari kebarangkalian bahawa
(i) satu nombor yang kurang daripada enam dan satu kad merah dipilih,
(ii) satu nombor lebih daripada tiga atau satu kad ungu dipilih.

Jawapan:
(a)

Penyelesaian:
(a)

(b)

\begin{array}{l} (i) \\ Ruang sampel satu nombor yang kurang daripada enam dan satu kad merah dipilih \\ {(1, R), (2, R), (3, R), (4, R), (5, R)} \\ Kebarangkalian = \frac{5}{18} \\ (ii) \\ Ruang sampel satu nombor lebih daripada tiga atau satu kad ungu dipilih \\ {(4, Y), (5, Y), (6, Y), (4, R), (5, R), (6, R), (4, P), (5, P), (6, P) \\ , (1, P), (2, P), (3, P)} \\ Kebarangkalian = \frac{12}{18} \\ = \frac{2}{3} \end{array}

Soalan 6:
Sekeping duit syiling dan sebiji dadu dilambung serentak. Dengan menyenaraikan sampel bagi semua kesudahan peristiwa yang mungkin, cari kebarangkalian

(a) muka kepala dan nombor ganjil diperoleh,

(b) muka kepala atau nombor lebih besar daripada 4 diperoleh.

Penyelesaian:

\begin{array}{l} (a) \\ Ruang sampel muka kepala dan nombor ganjil \\ {(K, 1), (K, 3), (K, 5)} \\ Kebarangkalian = \frac{3}{12} \\ = \frac{1}{4} \\ (b) \\ Ruang sampel muka kepala atau nombor lebih besar daripada 4 \\ {(K, 1), (K, 2), (K, 3), (K, 4), (K, 5), (K, 6), (A, 5), (A, 6)} \\ Kebarangkalian = \frac{8}{12} \\ = \frac{2}{3} \end{array}

7.4.4 Kebarangkalian II, SPM Praktis (Kertas 1)

Posted on May 11, 2020 by Myhometuition

Soalan 7:
Seorang penjual buah-buahan hendak membuat semakan bilangan epal busuk dalam setiap kotak. Jadual di bawah menunjukkan bilangan epal busuk dalam setiap kotak.

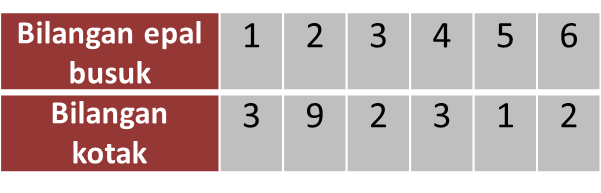Diberi bahawa terdapat 55 kotak epal. Jika satu kotak dipilih secara rawak, apakah kebarangkalian bahawa kotak itu tidak mengandungi epal busuk?

Penyelesaian:

\begin{array}{l} Bilangan kotak tidak mengandungi epal busuk \\ = 55 - (3 + 9 + 2 + 3 + 1 + 2) \\ = 55 - 20 \\ = 35 \\ Kebarangkalian = \frac{35}{55} = \frac{7}{11} \end{array}

Soalan 8:
Sebuah kelas sains tingkatan 5 mempunyai 15 orang pelajar lelaki dan beberapa orang pelajar perempuan. Seorang pelajar dipilih secara rawak daripada kelas itu. Kebarangkalian memilih seorang pelajar lelaki ialah

\frac{3}{5} .

Cari bilangan pelajar perempuan dalam kelas itu.

Penyelesaian:

\begin{array}{l} Katakan x ialah bilangan pelajar perempuan dalam kelas . \\ P (seorang pelajar perempuan) = 1 - \frac{3}{5} \\ = \frac{2}{5} \\ \frac{x}{15 + x} = \frac{2}{5} \\ 5 x = 30 + 2 x \\ 3 x = 30 \\ x = 10 \end{array}

7.4.3 Kebarangkalian II, SPM Praktis (Kertas 1)

Posted on May 11, 2020 by Myhometuition

Soalan 5:
Dalam sebuah syarikat, seramai 300 orang pekerja menaiki bas, 60 orang pekerja menaiki kereta dan selebihnya menunggang motosikal ke tempat kerja. Seorang pekerja dipilih secara rawak. Kebarangkalian memilih seorang pekerja yang menaiki bas ke tempat kerja ialah ⅔.
Cari kebarangkalian memilih seorang pekerja yang tidak menunggang motosikal untuk ke tempat kerja itu.

Penyelesaian:

\begin{array}{l} Katakan y ialah bilangan pekerja menunggang motosikal ke tempat kerja . \\ P (menaiki bas) = \frac{2}{3} \\ \frac{Bilangan pekerja (menaiki bas)}{Jumlah bilangan pekerja} = \frac{2}{3} \\ \frac{300}{300 + 60 + y} = \frac{2}{3} \\ 900 = 720 + 2 y \\ 2 y = 180 \\ y = 90 \\ Kebarangkalian = \frac{300 + 60}{360 + 90} \\ = \frac{360}{450} \\ = \frac{4}{5} \end{array}

Soalan 6:
Sebuah kotak mengandungi 18 keping kad hitam dan 8 keping kad biru. Fanny memasukkan lagi 2 keping kad hitam dan 4 keping kad biru ke dalam kotak itu. Sekeping kad dipilih secara rawak daripada kotak itu.
Apakah kebarangkalian sekeping kad hitam akan dipilih?

Penyelesaian:

\begin{array}{l} Jumlah bilangan kad yang baru dalam kotak \\ = (18 + 2) + (8 + 4) \\ = 32 \\ Kebarangkalian sekeping kad hitam dipilih \\ Kebarangkalian = \frac{18 + 2}{32} \\ = \frac{20}{32} \\ = \frac{5}{8} \end{array}

7.4.2 Kebarangkalian II, SPM Praktis (Kertas 1)

Posted on May 11, 2020 by Myhometuition

Soalan 3:
Sebuah kotak mengandungi 48 guli yang terdiri daripada guli merah dan guli hijau. Sebiji guli dipilih secara rawak dari kotak itu. Kebarangkalian sebiji guli merah dipilih ialah

\frac{1}{6} .

Berapakah bilangan guli merah yang perlu ditambah ke dalam kotak itu supaya kebarangkalian sebiji guli merah dipilih ialah

\frac{1}{2} .

Penyelesaian:

\begin{array}{l} Bilangan guli merah dalam kotak itu \\ = \frac{1}{6} \times 48 \\ = 8 \\ Katakan y ialah bilangan guli merah yang perlu ditambah ke dalam kotak itu . \\ P (guli merah) = \frac{1}{2} \\ \frac{8 + y}{48 + y} = \frac{1}{2} \\ 16 + 2 y = 48 + y \\ 2 y - y = 48 - 16 \\ y = 32 \\ ∴ Bilangan guli merah yang perlu ditambah = 32 \end{array}

Soalan 4:
Sebuah kotak mengandungi 5 keping kad merah, 3 keping kad kuning dan beberapa keping kad hijau. Sekeping kad dipilih secara rawak daripada kotak itu. Diberi kebarangkalian memilih kad kuning ialah

\frac{1}{6}

, cari kebarangkalian memilih sekeping kad yang bukan warna hijau.

Penyelesaian:

\begin{array}{l} P (kad kuning) = \frac{n (kad kuning)}{n (S)} \\ \frac{1}{6} = \frac{3}{n (S)} \\ n (S) = 3 \times 6 \\ = 18 \\ n (bukan kad hijau) = 5 + 3 = 8 \\ P (bukan kad hijau) = \frac{8}{18} \\ = \frac{4}{9} \end{array}