4.4.1 Pengungkapan Suatu Vektor sebagai Gabungan Linear Vektor yang lain (Contoh)
Contoh:
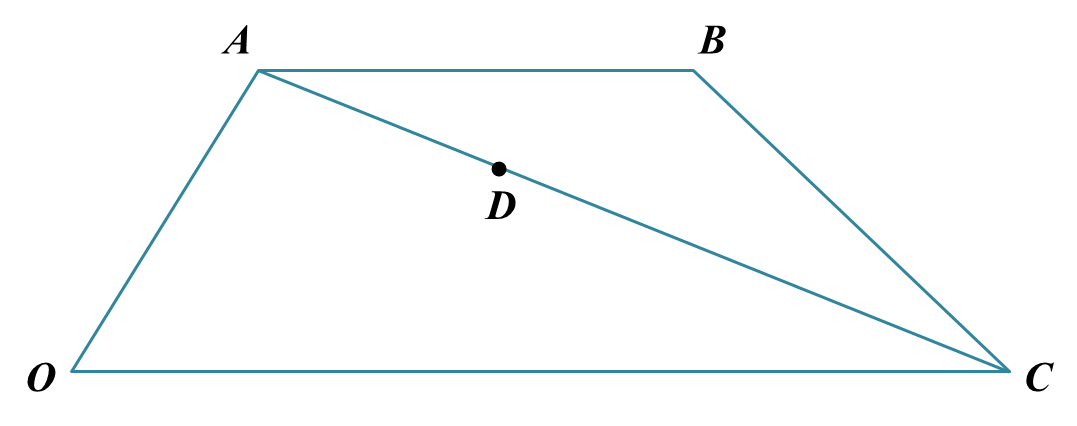
Rajah di bawah menunjukkan sebuah segiempat selari ABCD. Titik Q terletak pada garis lurus AB dan titik S terletak pada garis lurus DC. Garis lurus AS dipanjangkan ke titik T dengan keadaan AS = 2ST.
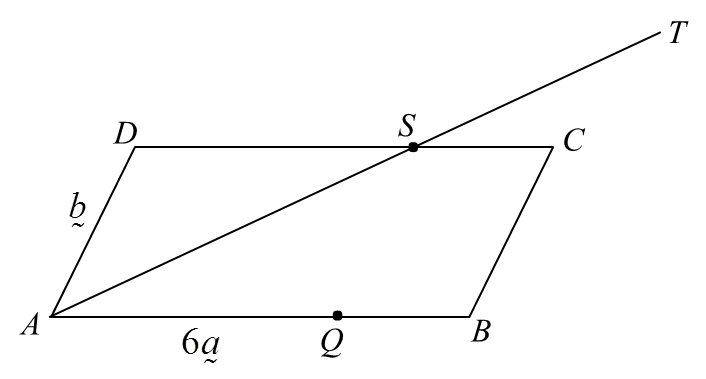
Diberi bahawa AQ : QB = 3 : 1, DS : SC = 3 : 1,
→AQ=6a˜ dan →AD=b˜
(a) Ungkapan dalam sebutan a˜ dan b˜:
(i) →AS (ii) →QC
(b) Seterusnya, tunjukkan titik Q, C dan T adalah segaris.
Penyelesaian:
(a)(i)
→AS=→AD+→DS=→AD+→AQ←AQ:QB= 3:1 dan DS:SC= 3:1∴
(a)(ii)
(b)
 Rajah
Rajah Rajah
Rajah Rajah
Rajah