Soalan 5:
Rajah di bawah menunjukkan sebuah segi tiga KLM.
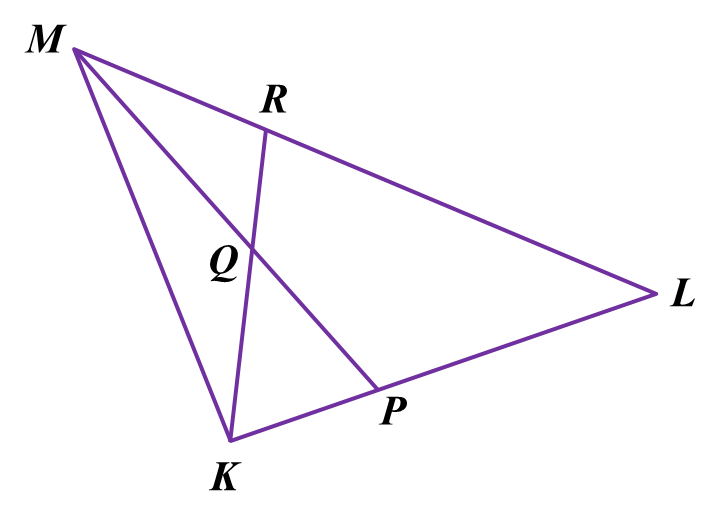
Diberi KP:PL=1:2, LR:RM=2:1, →KP=2x˜, →KM=3y˜.(a) Ungkapkan dalam sebutan x˜ dan y˜,(i) →MP(ii) →MR(b) Diberi x˜=2i˜ dan y˜=−i˜+4j˜, cari →|MR|.(c) Diberi →MQ=h→MP dan →QR=n→KR, dengan keadaan h dan n ialah pemalar, cari nilai h dan nilai n.
Penyelesaian:
(a)(i)
→MP=→MK+→KP =−3y˜+2x˜ =2x˜−3y˜
(a)(ii)
→MR=13→ML =13(→MK+→KL) =13(−3y˜+6x˜) =2x˜−y˜
(b)
→MR=2(2i˜)−(−i˜+4j˜) =4i˜+i˜−4j˜ =5i˜−4j˜|→MR|=√52+(−4)2 =√41 unit
(c)
→MQ+→QR=→MRh→MP+n→KR=→MRh(2x˜−3y˜)+n(→KM+→MR)=2x˜−y˜h(2x˜−3y˜)+n(3y˜+2x˜−y˜)=2x˜−y˜2hx˜−3hy˜+2nx˜+2ny˜=2x˜−y˜(2h+2n)x˜+(−3h+2n)y˜=2x˜−y˜2h+2n=2..........(1)−3h+2n=−1..........(2)(1)−(2):5h=3 h=35Dari (1):h+n=1 35+n=1 n=1−35 n=25
Rajah di bawah menunjukkan sebuah segi tiga KLM.

Diberi KP:PL=1:2, LR:RM=2:1, →KP=2x˜, →KM=3y˜.(a) Ungkapkan dalam sebutan x˜ dan y˜,(i) →MP(ii) →MR(b) Diberi x˜=2i˜ dan y˜=−i˜+4j˜, cari →|MR|.(c) Diberi →MQ=h→MP dan →QR=n→KR, dengan keadaan h dan n ialah pemalar, cari nilai h dan nilai n.
Penyelesaian:
(a)(i)
→MP=→MK+→KP =−3y˜+2x˜ =2x˜−3y˜
(a)(ii)
→MR=13→ML =13(→MK+→KL) =13(−3y˜+6x˜) =2x˜−y˜
(b)
→MR=2(2i˜)−(−i˜+4j˜) =4i˜+i˜−4j˜ =5i˜−4j˜|→MR|=√52+(−4)2 =√41 unit
(c)
→MQ+→QR=→MRh→MP+n→KR=→MRh(2x˜−3y˜)+n(→KM+→MR)=2x˜−y˜h(2x˜−3y˜)+n(3y˜+2x˜−y˜)=2x˜−y˜2hx˜−3hy˜+2nx˜+2ny˜=2x˜−y˜(2h+2n)x˜+(−3h+2n)y˜=2x˜−y˜2h+2n=2..........(1)−3h+2n=−1..........(2)(1)−(2):5h=3 h=35Dari (1):h+n=1 35+n=1 n=1−35 n=25