3.4 SPM Practis (Soalan Pendek)
Soalan 1:
Senaraikan semua subset bagi set P = {r, s}.
Penyelesaian:
Terdapat 2 unsur dalam set P, jadi bilangan subset bagi set P ialah 2n = 22= 4.
Set P = {r, s}
Maka subset bagi set P = {r}, {s}, {r, s}, { }
Soalan 2:
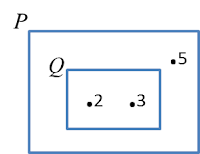
Rajah di atas menunjukkan gambar rajah Venn dengan set semesta, ξ = Q U
P. Senaraikan semua subset bagi set P.
Penyelesaian:
Terdapat 3 unsur dalam set P, jadi bilangan subset bagi set P ialah 2n = 23 = 8.
Set P = {2, 3, 5}
Maka subset bagi set P = { }, {2}, {3}, {5}, {2, 3}, {2, 5}, {3, 5}, {2, 3, 5}.
Soalan 3:
Diberi bahawa set semesta, ξ = {x : 30 ≤ x < 42, x ialah integer} dan set P= {x : x ialah nombor dengan keadaan hasil tambah dua digitnya ialah nombor genap}.
Carikan set P’.
Penyelesaian:
ξ = {30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41}
P = {31, 33, 35, 37, 39, 40}
Maka P’= {30, 32, 34, 36, 38, 41}
Soalan 4:
Diberi bahawa set semesta, ξ = {x : 3 < x ≤ 16, x ialah integer},
Set A = {4, 11, 13, 16},
Set B = {x : x ialah nombor ganjil} dan
Set C = {x : x ialah gandaan bagi 3}.
Unsur bagi set (A∪C)'
Penyelesaian:
ξ = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}
A = {4, 11, 13, 16}
B = {5, 7, 9, 11, 13, 15}
C = {6, 9, 12, 15}