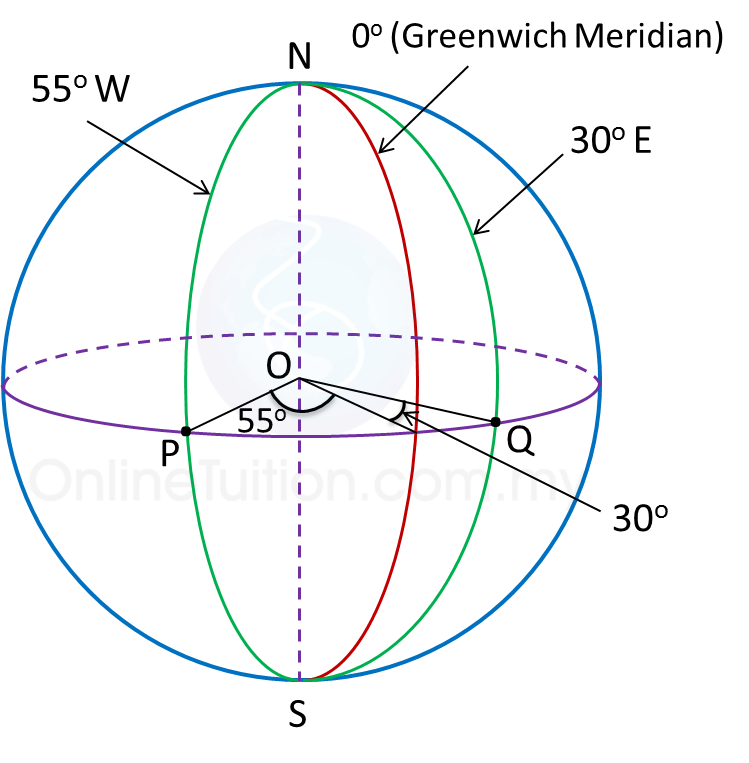
Question 4:
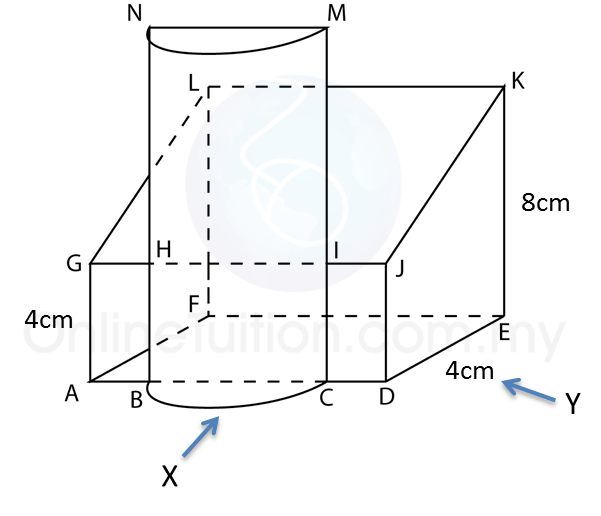 Solution:
Solution:
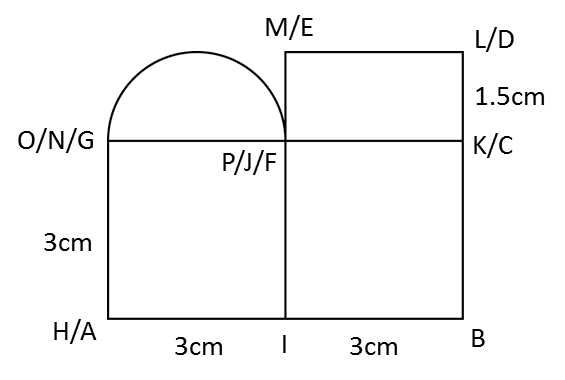
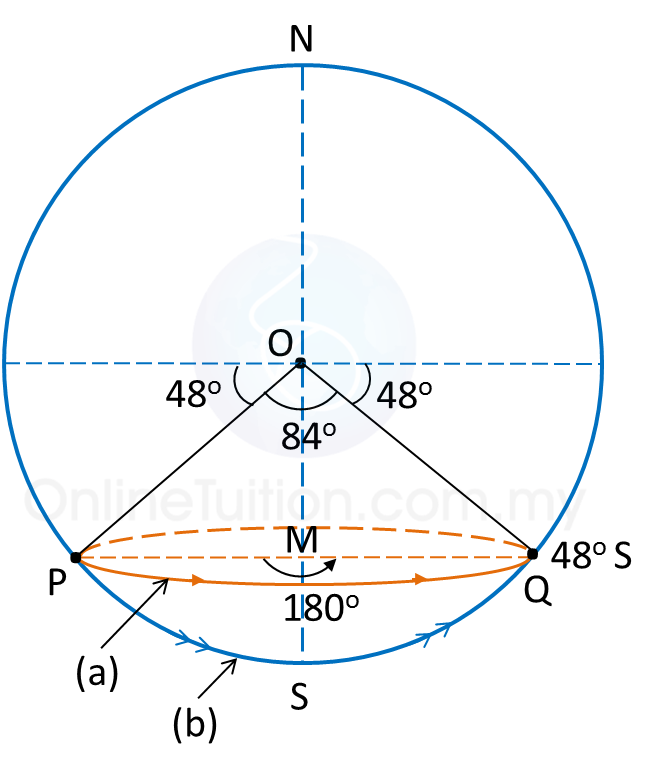
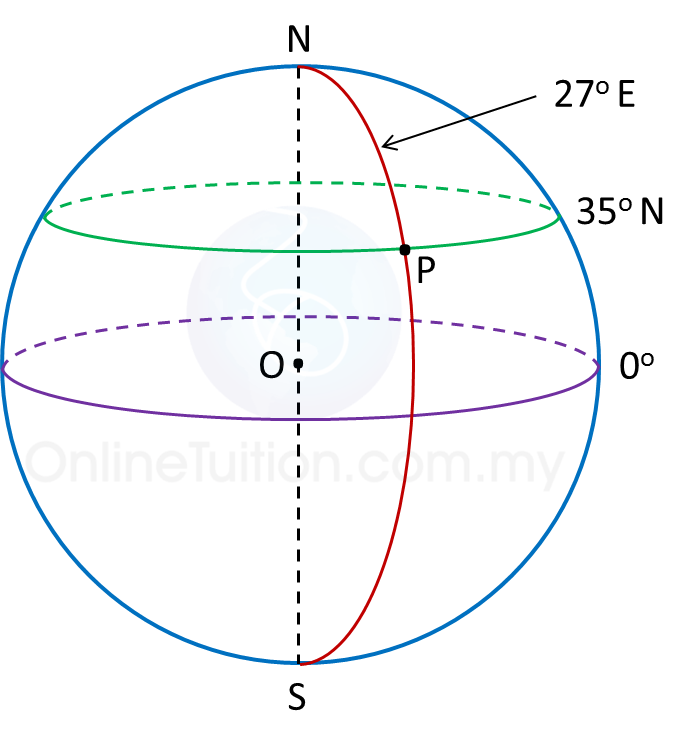
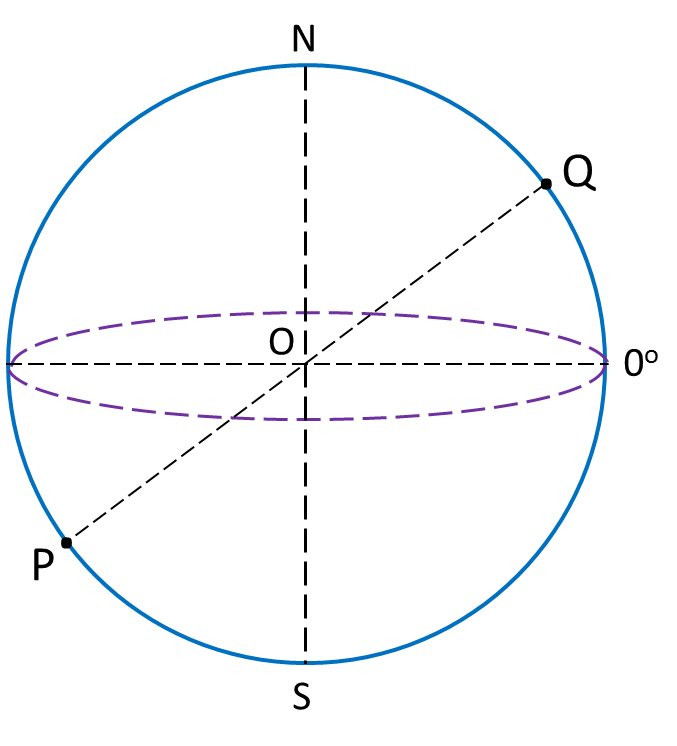
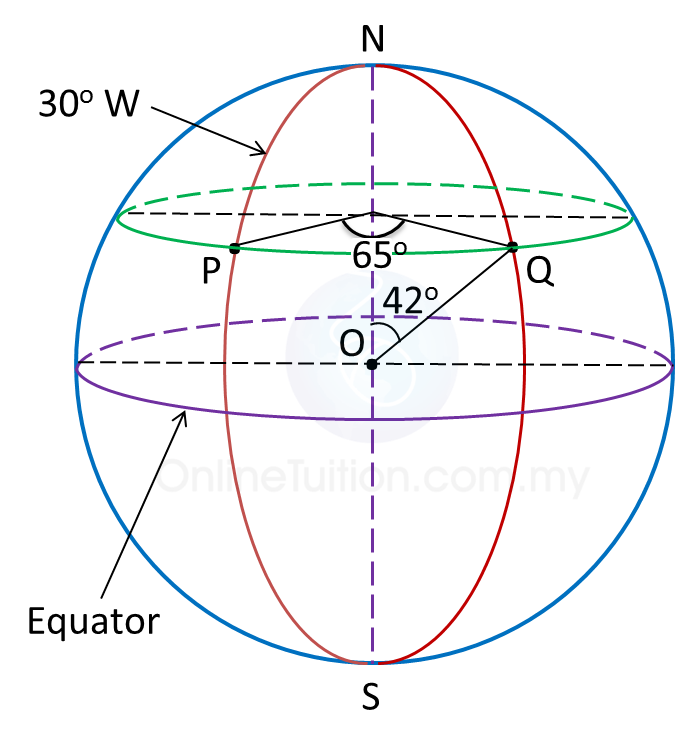
(a)
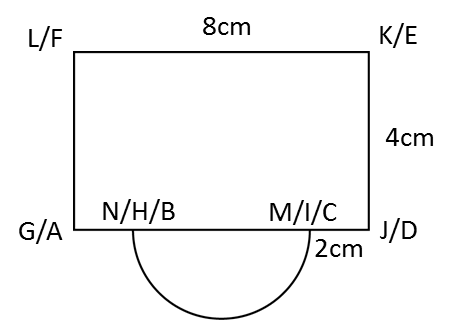
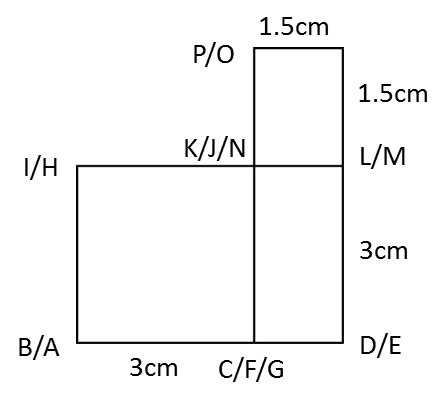
(b)
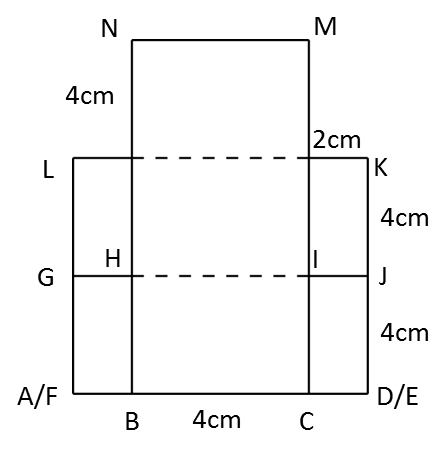
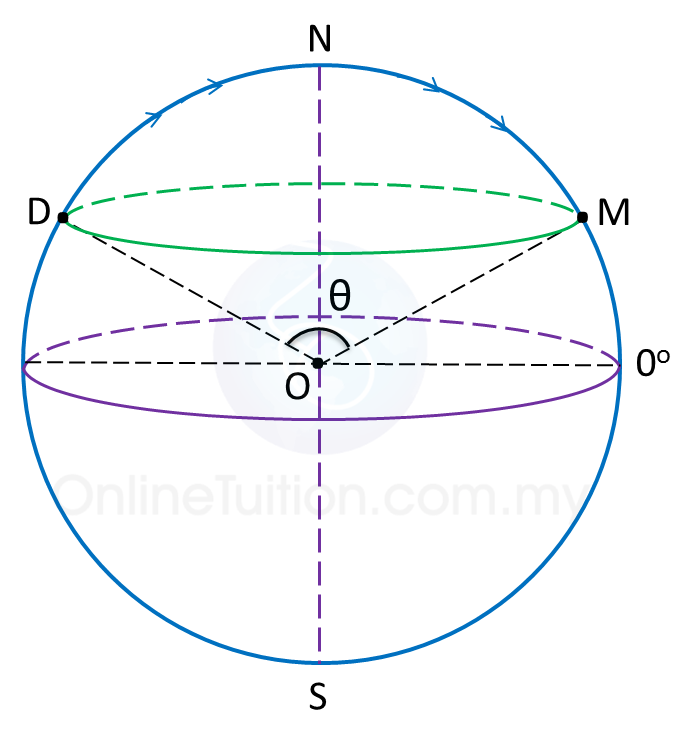
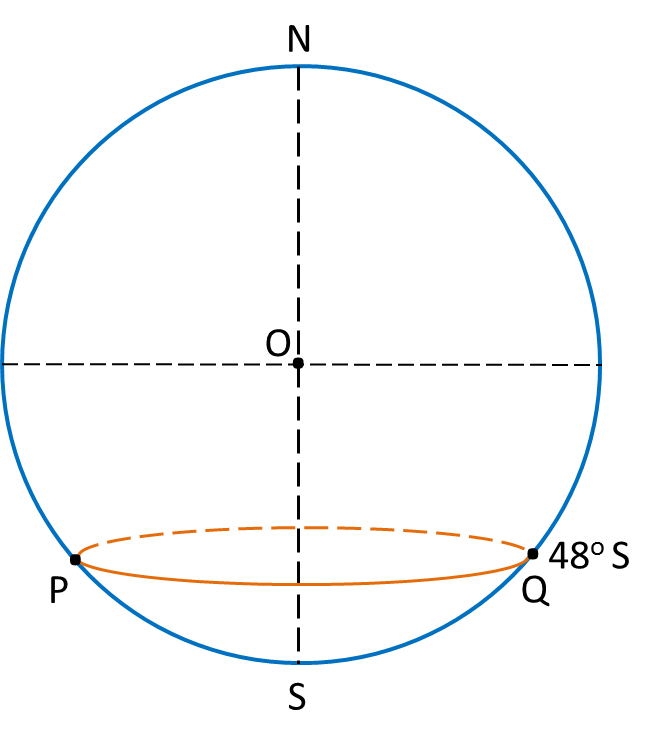
(c)


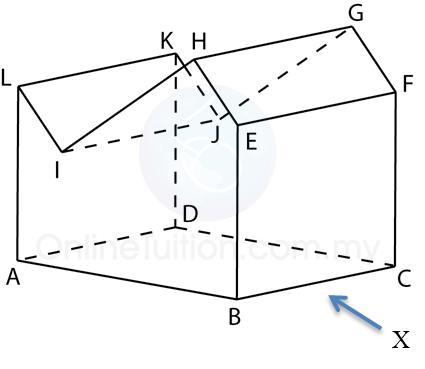
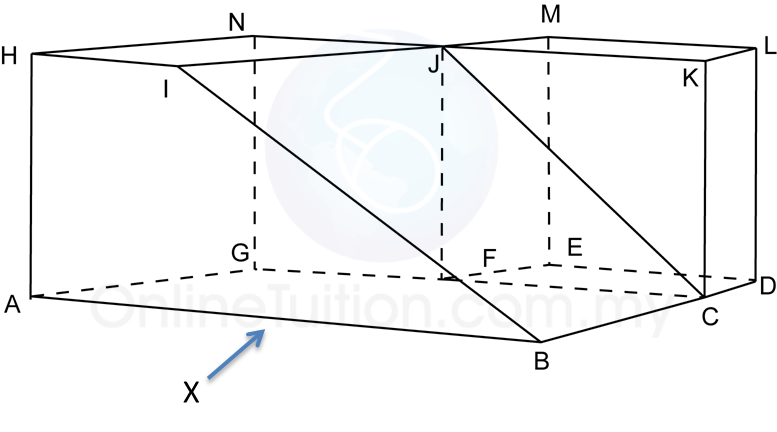
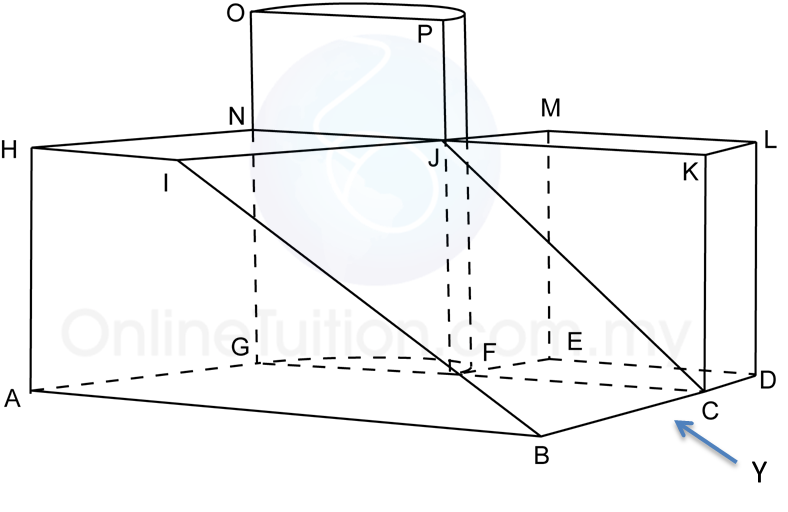
The diagram above shows a solid consisting of a right prism and a half-cylinder which are joined at the plane HICB. The base ABCDEF is on a horizontal plane. The rectangle LKJG is an inclined plane. The vertical plane JDEK is the uniform cross-section of the prism. AB = CD = 2 cm. BC = 4 cm. CM = 12 cm.
Draw to full scale
(a) The plan of the solid
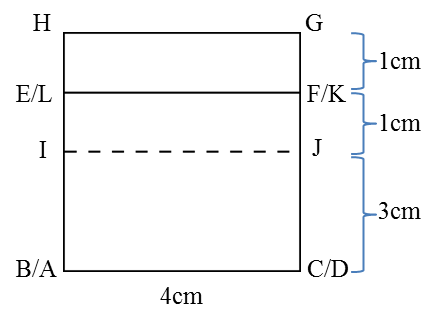
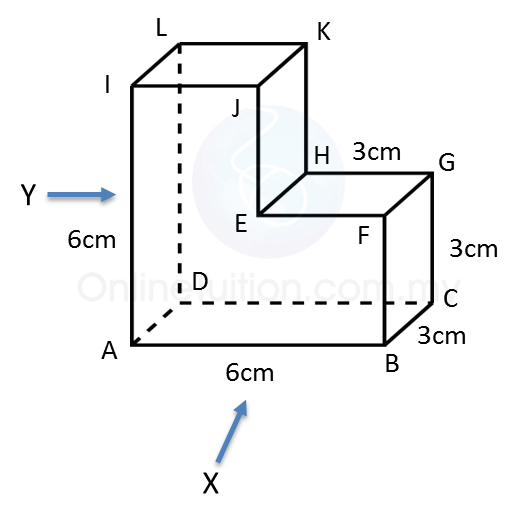
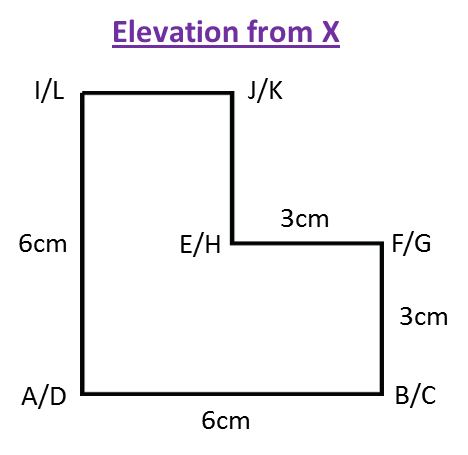
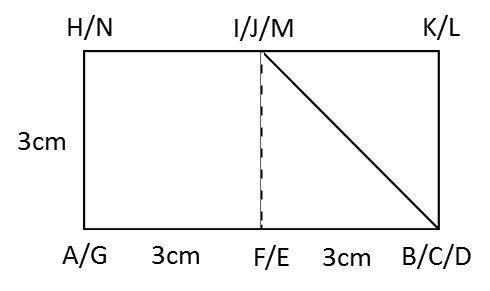
(b) The elevation of the solid on a vertical plane parallel to ABCD as viewed from X.
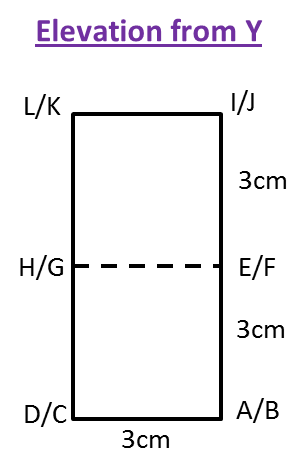
(c) The elevation of the solid on a vertical plane parallel to DE as viewed from Y.
(a)

(b)

(c)