8.1 Tangen kepada Bulatan
1. Tangen kepada bulatan ialah garis lurus yang menyentuh bulatan itu pada satu titik sahaja. Titik tersebut dipanggil titik sentuhan.
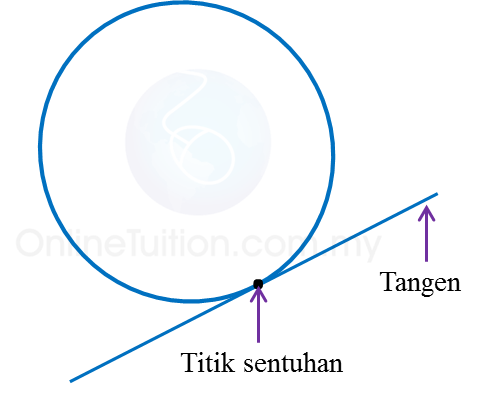
2. Jejari yang melalui titik sentuhan tangen adalah berserenjang dengan tangen itu.
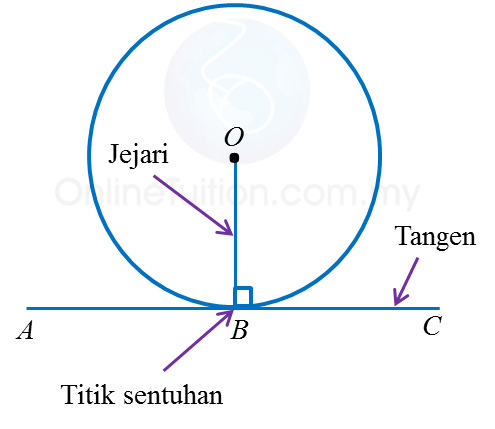

Jika ABC ialah tangen kepada bulatan di B, maka ∠ABO = ∠CBO = 90o.
8.1.1 Sifat-sifat Berkaitan dengan Dua Tangen kepada Suatu Titik di Luar Bulatan
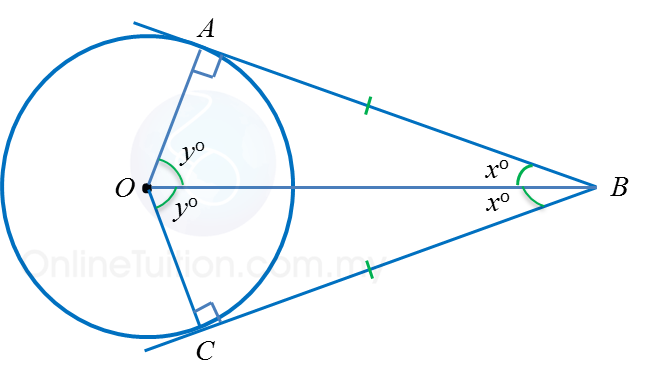

Dalam rajah di atas, BA dan BC ialah dua tangen dari satu titik luar B. Sifat-sifat bagi tangennya adalah berikut.
Contoh 1:
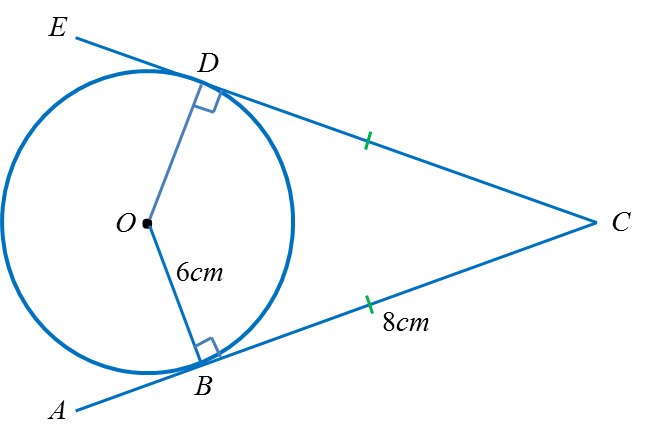
Rajah di atas menunjukkan sebuah bulatan dengan pusat O. ABC dan CDE ialah dua tangen kepada bulatan di titik B dan D masing-masing. Cari panjang OC
Penyelesaian:
OC2= OB2 + BC2 ← (Teori Pythagoras)
= 62+ 82
= 100
OC = √100 = 10 cm
Contoh 2:
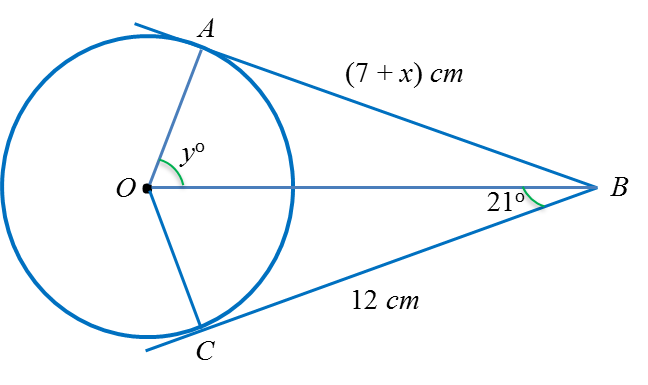

Dalam rajah di atas, AB dan BC ialah dua tangen kepada bulatan dengan pusat O. Hitung nilai bagi
(a) x (b) y
Penyelesaian:
(a) AB = BC
7 + x = 12
x = 5
(b)
∠OBA = ∠OCB = 21o
∠OCB = 90o ← (OC berserenjang dengan CB)
yo = 180o – 21o – 90o
y = 69Contoh 3:
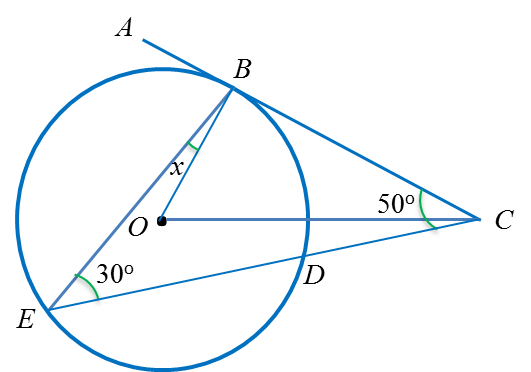

Dalam rajah di atas, ABC ialah tangen kepada bulatan dengan pusat O di titikt B. CDE ialah garis lurus. Cari nilai bagi x.
Penyelesaian:
∠CBO = 90o ← (OB berserenjang dengan BC)
Dalam ∆ BCE,
xo = 180o – 30o – 50o – 90o
x = 10o