Bab 12 Janjang

Posted on May 21, 2016 by user

1.2.2 Menetukan Sebutan Tertentu dan Bilangan Sebutan dalam Suatu Janjang Geometri

(C) Sebutan Tertentu dalam Suatu Janjang Geometri

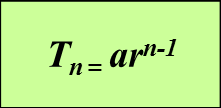
a = sebutan pertama
r = nisbah sepunya

n = bilangan sebutan

T_n = sebutan ke-n

Contoh:

Cari sebutan yang diberi bagi setiap janjang geometri yang berikut.

(a) 8 ,4 ,2 ,...... T₈

(b)

\frac{16}{27}, \frac{8}{9}, \frac{4}{3}, .....

, T₆

Penyelesian:

T_n = arⁿ^-1

T₁ = ar^1-1 = ar⁰ = a ← (sebutan pertama)

T₂ = ar^2-1 = ar¹ = ar ← (sebutan kedua)

T₃ = ar^3-1 = ar² ← (sebutan ketiga)

T₄ = ar^4-1 = ar³ ← (sebutan keempat)

(a)

\begin{array}{l} 8, 4, 2, ..... \\ a = 8, r = \frac{4}{8} = \frac{1}{2} \\ T_{8} = a r^{7} \\ T_{8} = 8 {(\frac{1}{2})}^{7} = \frac{1}{16} \end{array}

(b)

\begin{array}{l} \frac{16}{27}, \frac{8}{9}, \frac{4}{3}, ..... \\ a = \frac{16}{27} \\ r = \frac{T_{2}}{T_{1}} = \frac{\frac{16}{27}}{\frac{8}{9}} = \frac{2}{3} \\ T_{6} = a r^{5} \\ = \frac{16}{27} {(\frac{2}{3})}^{5} = \frac{512}{6561} \end{array}

(D) Bilangan Sebutan dalam Suatu Janjang Geometri

Tip pintar: Bilangan sebutan dalam suatu janjang geometri dapat dicari jika sebutan terakhir
diketahui.

Contoh:

Cari bilangan sebutan bagi setiap janjang geometri yang berikut.

(a) 2, 4, 8, ….., 8192

(b)

\frac{1}{4}, \frac{1}{6}, \frac{1}{9}, ....., \frac{16}{729}

(c) –½, 1, –2, ….., 64

Penyelesian:

(a)

2, 4, 8, ….., 8192 ← (sebutan terakhir diberi)

a = 2

r = \frac{T_{2}}{T_{1}} = \frac{4}{2} = 2

T_n= 8192

arⁿ^-1= 8192 ← T_n = arⁿ^-1

(2)(2)ⁿ^-1 = 8192

2ⁿ^-1 = 4096

2ⁿ^-1 = 2¹²

n– 1 = 12

n = 13

(b)

\begin{array}{l} \frac{1}{4}, \frac{1}{6}, \frac{1}{9}, ....., \frac{16}{729} \\ a = \frac{1}{4}, r = \frac{\frac{1}{6}}{\frac{1}{4}} = \frac{2}{3} \\ T_{n} = \frac{16}{729} \\ a r^{n - 1} = \frac{16}{729} \\ (\frac{1}{4}) {(\frac{2}{3})}^{n - 1} = \frac{16}{729} \\ {(\frac{2}{3})}^{n - 1} = \frac{16}{729} \times 4 \\ {(\frac{2}{3})}^{n - 1} = \frac{64}{729} \\ {(\frac{2}{3})}^{n - 1} = {(\frac{2}{3})}^{6} \\ ∴ n - 1 = 6 \\ n = 7 \end{array}

(c)

\begin{array}{l} - \frac{1}{2}, 1, - 2, ....., 64 \\ a = - \frac{1}{2}, r = \frac{- 2}{1} = - 2 \\ T_{n} = 64 \\ a r^{n - 1} = 64 \\ (- \frac{1}{2}) {(- 2)}^{n - 1} = 64 \end{array}

T_n= 64

arⁿ^-1= 64

(–½)(–2)ⁿ^-1 = 64

(–2)ⁿ^-1 = 64 × –2

(–2)ⁿ^-1 = –128

(–2)ⁿ^-1 = (–2)⁷

n– 1 = 7

n = 8

(E) Tiga sebutan Berturutan dalam suatu janjang geometri (J.G.)

Jika e, f dan g adalah 3 sebutan berturutan dalam suatu janjang geometri (JG), maka

\frac{g}{f} = \frac{f}{e}

Contoh:

Jika p + 20, p − 4, p −20 adalah 3 sebutan berturutan dalam suatu janjang geometri, cari niali p.

Penyelesian:

\frac{p - 20}{p - 4} = \frac{p - 4}{p + 20}

(p + 20)(p – 20) = (p – 4)(p – 4)

p²– 400 = p² – 8p + 16

8p = 416

p = 52