Bab 15 Vektor

Posted on May 24, 2016 by user

4.3 Penambahan dan Penolakan Vektor

4.3.1 Penambahan Vektor

1. Penambahan dua vektor,

$\underset{˜}{u} dan \underset{˜}{v}$ , boleh ditulis sebagai

$\underset{˜}{u} + \underset{˜}{v}$ . Hasil tambah ini merupakan suatu vektor, yang dinamakan vector paduan.

2. Apabila dua vektor yang sama ditambah, vector paduan yang terhasil mempunyai

(a) arah yang sama dengan kedua-dua vektor itu,

(b) magnitude yang sama dengan hasil tambah magnitud kedua-dua vektor itu.

(A) Penambahan Vektor Paduan Dua Vektor Tidak Selari

1. Penambahan dua vektor yang tidak selari,

$\underset{˜}{u} dan \underset{˜}{v}$ , boleh ditunjukkan dengan dua hukum.

(i) Hukum Segitiga

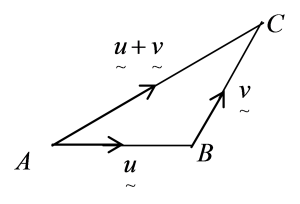
Vektor paduan

$\underset{˜}{u} + \underset{˜}{v}$ yang terhasil ialah AC.

(ii) Hukum Segiempat Selari

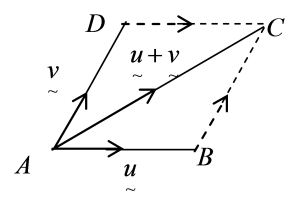
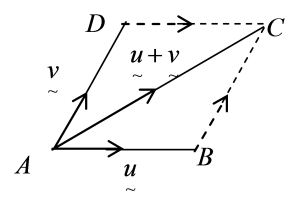
Vektor paduan

$\underset{˜}{u} + \underset{˜}{v}$ yang terhasil ialah AC.

Contoh 1:

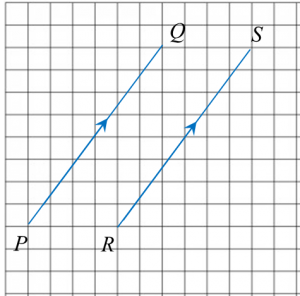
Cari

(a) vector paduan hasil tambah bagi dua vector selari yang di atas.

(b) magnitud bagi vector paduan.

Penyelesaian:

(a)

Vektor paduan

= hasil tambah dua vektor

$= \vec{P Q} + \vec{R S}$

(b)

Magnitud bagi vector paduan

$\begin{array}{l} = | \vec{P Q} | + | \vec{R S} | \\ = | \sqrt{6^{2} + 8^{2}} | + | \sqrt{6^{2} + 8^{2}} | \\ = 10 + 10 \\ = 20 units \end{array}$

Contoh 2:

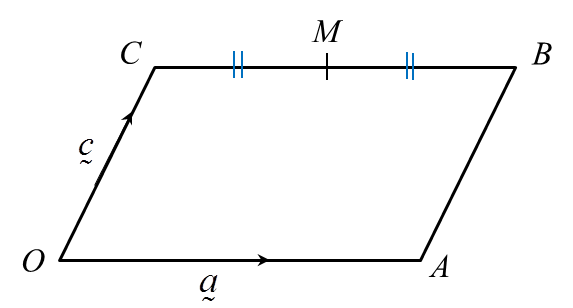
Rajah di atas menunjukkan suatu segiempat selari OABC. M adalah titik tengah BC. Vektor

$\vec{O A} = \underset{˜}{a} dan \vec{O C} = \underset{˜}{c} .$ Cari setiap vektor yang berikut dalam sebutan

$\underset{˜}{a} dan \underset{˜}{c} .$

$\begin{array}{l} (a) \vec{O B} \\ (b) \vec{M B} \\ (c) \vec{O M} \end{array}$

Penyelesaian:

(a)

$\begin{array}{l} \vec{O B} = \vec{O A} + \vec{A B} \leftarrow Hukum segitiga \\ = \vec{O A} + \vec{O C} \leftarrow \vec{A B} = \vec{O C} \\ = \underset{˜}{a} + \underset{˜}{c} \end{array}$

(b)

$\begin{array}{l} \vec{M B} = \frac{1}{2} \vec{C B} \leftarrow M adalah titik tengah C B \\ = \frac{1}{2} \vec{O A} \\ = \frac{1}{2} \underset{˜}{a} \end{array}$

(c)

$\begin{array}{l} \vec{O M} = \vec{O C} + \vec{C M} \leftarrow Hukum segitiga \\ = \vec{O C} + \vec{M B} \leftarrow \vec{C M} = \vec{M B} \\ = \underset{˜}{c} + \frac{1}{2} \underset{˜}{a} \end{array}$