Bab 7 Statistik

Posted on May 31, 2016 by user

7.2 Sukatan Serakan (Bahagian 3)

7.2c Varians dan Sisihan Piawai

1. Varians ialah sukatan minbagi kuasa dua sisihan-sisihan daripada min.

2. Sisihan piawai merujuk kepada punca kuasa dua positif bagi varians.

(A) Data Tak Terkumpul

$Varians, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2}$

$Sisihan piawai, σ = \sqrt{varians}$

Contoh 1:

Cari varians dan sisihan piawai bagi set data,

15, 17, 21, 24 dan 31

Penyelesaian:

$\begin{array}{l} Varians, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2} \\ σ^{2} = \frac{15^{2} + 17^{2} + 21^{2} + 24^{2} + 31^{2}}{5} \\ - {(\frac{15 + 17 + 21 + 24 + 31}{5})}^{2} \\ σ^{2} = \frac{2492}{5} - {21.6}^{2} \\ σ^{2} = 31.84 \\ Sisihan piawai, σ = \sqrt{varians} \\ σ = \sqrt{31.84} \\ σ = 5.642 \end{array}$

(B) Data Terkumpul (tanpa Selang Kelas)

$Varians, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2}$

$Sisihan piawai, σ = \sqrt{varians}$

Contoh 2:

Data di bawah menunjukkan bilangan kanak-kanak oleh 30 keluarga:

Bilangan kanak-kanak	2	3	4	5	6	7	8
Kekerapan	6	8	5	3	3	3	2

Cari varians dan sisihan piawai bagi set data.

Penyelesaian:

$\begin{array}{l} Min \bar{x} = \frac{\sum f x}{\sum f} \\ = \frac{(6) (2) + (8) (3) + (5) (4) + (3) (5) + (3) (6) + (3) (7) + (2) (8)}{6 + 8 + 5 + 3 + 3 + 3 + 2} \\ = \frac{126}{30} = 4.2 \\ \frac{\sum f x^{2}}{\sum f} \\ = \frac{(6) {(2)}^{2} + (8) {(3)}^{2} + (5) {(4)}^{2} + (3) {(5)}^{2} + (3) {(6)}^{2} + (3) {(7)}^{2} + (2) {(8)}^{2}}{6 + 8 + 5 + 3 + 3 + 3 + 2} \\ = \frac{634}{30} = 21.13 \end{array}$

$\begin{array}{l} Varians, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2} \\ σ^{2} = 21.133 - {4.2}^{2} \\ σ^{2} = 3.493 \\ Sisihan piawai, σ = \sqrt{varians} \\ σ = \sqrt{3.493} \\ σ = 1 .869 \end{array}$

(C) Data Terkumpul (dengan Selang Kelas)

$Varians, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2}$

$Sisihan piawai, σ = \sqrt{varians}$

Contoh 3:

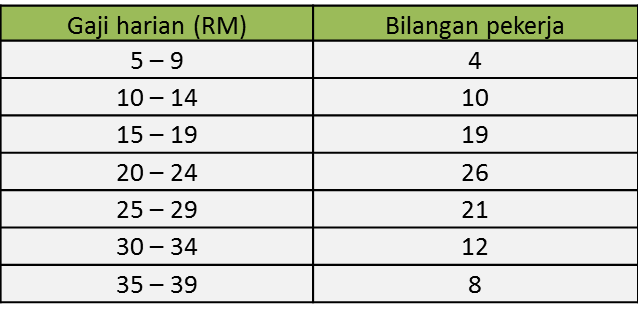
Hitung min gaji harian dan sisihan piawai.

Penyelesaian:

Gaji harian (RM)	Bilangan pekerja, f	Nilai tengah, x	fx	fx²
10 – 14	40	12	480	5760
15 – 19	25	17	425	7225
20 – 24	15	22	330	7260
25 – 29	12	27	324	8748
30 – 34	8	32	256	8192
Total	100		1815	37185

$\begin{array}{l} Min \bar{x} = \frac{\sum f x}{\sum f} \\ Min gaji harian = \frac{1815}{100} = 18.15 \end{array}$

$\begin{array}{l} Varians, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2} \\ Sisihan piawai, σ = \sqrt{varians} \\ σ^{2} = \frac{37185}{100} - {18.15}^{2} \\ σ^{2} = 42.43 \\ σ = \sqrt{42.43} \\ σ = 6 .514 \end{array}$