Bab 8 Sukatan Membulat

Posted on May 29, 2016 by user

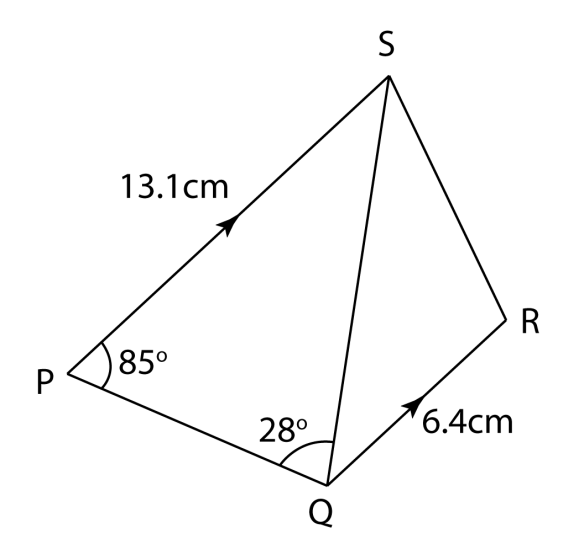
8.5.4 Sukatan Membulat, SPM Praktis (Kertas 2)

Soalan 4:

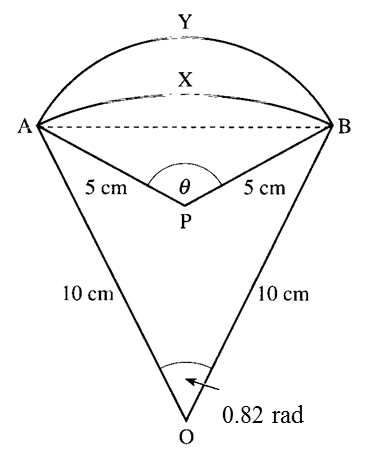
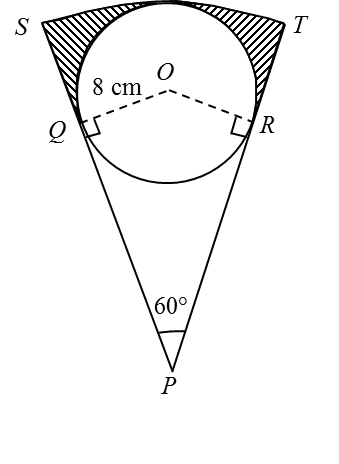
Dalam rajah di atas, AXB ialah lengkok sebuah bulatan berpusat O dan jejari 10cm dengan ∠AOB = 0.82 radian. AYB ialah lengkok sebuah bulatan berpusat P dan jejari 5cm dengan ∠APB = θ. Hitung:

(a) Panjang perentas AB,

(b) nilai θ dalam radian,

Penyelesaian:

(a)

½ AB = sin 0.41 × 10 (tukar mode kalkulator kepada Rad)

½ AB = 3.99

Maka panjang perentas AB = 3.99 × 2 = 7.98cm.

(b)

Katakan ½θ = α, θ = 2α

\sin α = \frac{3.99}{5}

α = 0.924 rad

Maka θ = 0.924 × 2 = 1.848 rad

(c)

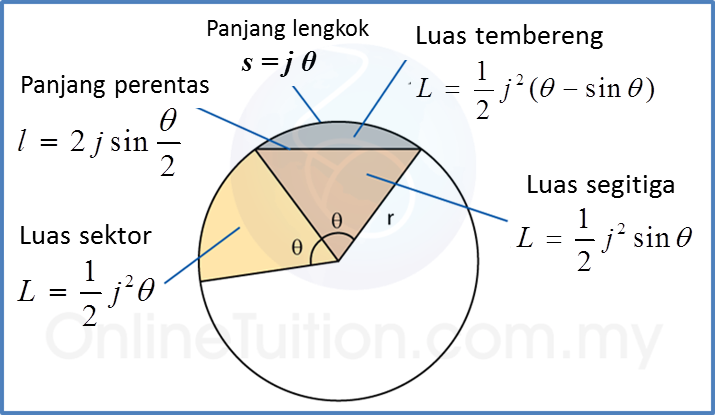
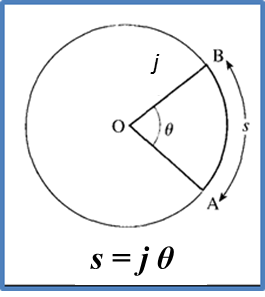
Guna s = jθ

Lengkok AXB = 10 × 0.82 = 8.2 cm

Lengkok AYB = 5 × 1.848 = 9.24 cm

Perbezaan panjang antara lengkok AYB dan lengkok AXB

= 9.24 – 8.2

= 1.04 cm

Bab 8 Sukatan Membulat

Posted on May 29, 2016 by user

8.5 Sukatan Membulat, SPM Praktis (Kertas 2)

Soalan 3:

Rajah di bawah menunjukkan bulatan PQRT, berpusat Odan jejari 5 cm. AQB ialah tangen kepada bulatan itu di Q . Garis lurus, AO dan BO, bersilang dengan bulatan itu masing-masing di P dan R. OPQR ialah sebuah rombus. ACB ialah lengkok sebuah bulatan berpusat O.

Hitungkan

(a) sudut x , dalam sebutan p,

(b) panjang, dalam cm , lengkok ACB,

(c) luas, dalam cm², kawasan berlorek.

Penyelesaian:

(a)

Rombus ada 4 sisi sama, maka OP = PQ = QR = OR = 5 cm

OR ialah jejari kepada bulatan, maka OR = OQ = 5 cm

Segitiga OQR dan segitiga OPQ adalah segitiga sisi sama,

Maka, ∠ QOR= ∠QOP = 60^o

∠ POR = 120^o

\begin{array}{l} x = 120^{o} \times \frac{π}{180^{o}} \\ x = \frac{2 π}{3} r a d \end{array}

(b)

\begin{array}{l} \cos ∠ A O Q = \frac{O Q}{O A} \\ \cos 60^{o} = \frac{5}{O A} \\ O A = 10 c m \end{array}

Panjang lengkok, ACB,

s = jθ

Panjang ACB = (10) (2π / 3)

Panjang ACB = 20.94 cm

(c)

Luas kawasan berlorek

= ½ (θ – sinθ) (tukar mode kalkulator kepada Rad)

= \frac{1}{2} {(10)}^{2} (\frac{2 π}{3} - \sin \frac{2 π}{3})

= 50 (2.094 – 0.866)

= 61.40 cm²

Bab 8 Sukatan Membulat

Posted on May 29, 2016 by user

8.4.2 Sukatan Membulat, SPM Praktis (Kertas 1)

Soalan 4:

Rajah di bawah menunjukkan sebuah bulatan berpusat O.

Panjang lengkok minor ialah 16 cm dan sudut bagi sector major AOB ialah 290^o.

Guna π = 3.142, cari

(a) nilai θ, dalam radian. (jawapan dalam empat angka bererti)

(b) panjang, dalam cm, jejari bulatan.

Penyelesaian:

(a)

Sudut sektor minor AOB

= 360^o– 290^o

= 70^o

= 70^o×

\frac{3.142}{180^{\circ}}

= 1.222 radian

(b)

Guna s = jθ

j × 1.222 = 16

jejari, j = 13.09 cm

Soalan 5:

Rajah di bawah menunjukkan sektor OPQ dengan pusat O dan sektor PXY berpusat P.

Diberi OQ = 8 cm, PY = 3 cm, ∠ XPY = 1.2 radian dan panjang lengkok PQ = 6cm,

hitung

(a) nilai θ, dalam radian,

(b) luas, dalam cm², kawasan berlorek.

Penyelesaian:

(a)

s = jθ

6 = 8θ

θ = 0.75 rad

(b)

Luas kawasan berlorek

= Luas sektor OPQ – Luas sektor PXY

= ½ (8)²(0.75) – ½ (3)² (1.2)

= 24 – 5.4

= 18.6 cm²

Soalan 6:

Rajah di bawah menunjukkan sebuah bulatan berpusat O dan berjejari 10 cm.

Diberi bahawa A, B dan C adalah titik dengan keadaan OA = AB dan ∠OAC = 90°, cari

[Guna π = 3.142]

(a) ∠BOC, dalam radian,

(b) luas, dalam cm², kawasan berlorek.

Penyelesaian:

(a)

Untuk ∆ OAC,

cos ∠AOC = 6/12

∠AOC = 1.047 rad (tukar mode kalkulator kepada RAD)

∠BOC = 1.047 rad

(b)

Luas kawasan berlorek

= Luas ∆ BOC – Luas ∆ AOC

= ½ (12)²(1.047) – ½ (6) (12) sin 1.047 (tukar mode kalkulator kepada RAD)

= 75.38 – 31.17

= 44.21 cm²

Bab 8 Sukatan Membulat

Posted on May 29, 2016 by user

8.5.2 Sukatan Membulat, SPM Praktis (Kertas 2)

Soalan 2:

Rajah di bawah menunjukkan dua bulatan. Bulatan yang lebih besar berpusat A dan berjejari 20 cm. Bulatan yang lebih kecil berpusat B dan berjejari 12 cm. Kedua-dua bulata bersentuh di titik R. Garis lurus PQ ialah tangen sepunya kepada kedua –dua bulatan itu di titik P dan titik Q.

[Guna π = 3.142]

Diberi bahawa ∠ PAR = θ radians,

(a) tunjukkan bahawa θ = 1.32 ( kepada dua tempat perpuluhan),

(b) hitung panjang, dalam cm, lengkok minor QR,

Penyelesaian:

(a)

\begin{array}{l} Dalam △ B S A \\ k o s θ = \frac{8}{32} = \frac{1}{4} \\ θ = 1.32 rad (2 t .p .) \end{array}

(b)

∠ QBR = 3.142 – 1.32 = 1.822 rad

Panjang lengkok minor QR

= 12 × 1.822

= 21.86 cm

(c)

P Q = \sqrt{32^{2} - 8^{2}} = 30.98 cm

Luas kawasan berlorek

= Luas trapezium PQBA – Luas sektor QBR – Luas sektor PAR

= (12 + 20) (30.98) – (12)² (1.822) – (20)²(1.32)

= 495.68 – 131.18 – 264

= 100.5 cm²

Bab 8 Sukatan Membulat

Posted on May 28, 2016 by user

8.4.1 Sukatan Membulat, SPM Praktis (Kertas 1)

Soalan 1:

Rajah di atas menunjukkan sektor OCB yang berjejari 13 cm dan berpusat O. panjang lengkok
CB = 5.2 cm. Cari

(a) ∠COB in radian,

(b) perimeter kawasan berlorek.

Penyelesaian:

(a)

s = jθ

5.2 = 13 (∠COB)

∠COB = 0.4 radian

(b)

\begin{array}{l} \cos ∠ C O B = \frac{O A}{O C} \\ \cos 0.4 = \frac{O A}{13} (tukar kalkulator kepada mode Rad) \\ O A = 11.97 cm \\ ∴ A B = 13 - 11.97 = 1.03 cm \\ C A = \sqrt{13^{2} - {11.97}^{2}} \\ C A = 5.07 cm \end{array}

Perimeter kawasan berlorek = 5.07 + 1.03 + 5.2 = 11.3 cm.

Soalan 2:

Rajah menunjukkan sektor AOB suatu bulatan, berpusat O dan berjejari 5 cm. Panjang
lengkok AB ialah 6cm. Cari luas

(a) sektor AOB,

(b) kawasan berlorek.

Penyelesaian:

(a)

Lengkok AB = 6cm

s = jθ

6 = 5θ

θ = 6/5 rad

Luas sektor AOB

= \frac{1}{2} j^{2} θ = \frac{1}{2} {(5)}^{2} (\frac{6}{5}) = 15 c m^{2}

(b)

Luas kawasan berlorek

\begin{array}{l} = \frac{1}{2} j^{2} (θ - \sin θ) (tukar kalkulator kepada mode Rad) \\ = \frac{1}{2} {(5)}^{2} (\frac{6}{5} - \sin \frac{6}{5}) \\ = 3.35 {cm}^{2} \end{array}

Soalan 3:

Rajah di bawah menunjukkan sektor QOR bagi sebuah bulatan berpusat O.

Diberi bahawa PS = 8 cm dan QP = PO = OS= SR = 5 cm.

Cari

(a) panjang, dalam cm, lengkok QR,

(b) luas, dalam cm², kawasan berlorek.

Penyelesaian:

(a) Panjang lengkok QR = jθ = 10 (1.75) = 17.5 cm

(b)

Luas kawasan berlorek

= Luas sektor QOR– Luas segitiga POS

= ½ (10)²(1.75) – ½ (5) (5) sin 1.75 (Kalkulator ditukar kepada mode RAD)

= 87.5 – 12.30

= 75.2 cm²

Bab 8 Sukatan Membulat

Posted on May 28, 2016 by user

8.5.1 Sukatan Membulat, SPM Praktis (Kertas 2)

Soalan 1:

Rajah menunjukkan sebuah bulatan berpusat O dan berjejari 8 cm terterap dalam sektor SPT bagi sebuah bulatan berpusat P. Garis lurus SP dan garis lurus TP adalah tangen kepada bulatan masing-masing di titik Q dan titik R.

[Guna π = 3.142]

Hitung

(a) panjang, dalam cm, lengkok ST,

(b) luas, dalam cm², kawasan berlorek.

Penyelesaian:

(a)

Bagi segitiga OPQ,

\begin{array}{l} \sin 30^{\circ} = \frac{8}{O P} \\ O P = \frac{8}{\sin 30^{\circ}} = 16 cm \end{array}

Jejari bagi sektor SPT = 16 + 8 = 24 cm

∠ S P T = 60 \times \frac{3.142}{180} = 1.047 radian

Panjang lengkok ST = 24 × 1.047 = 25.14 cm

(b)

Bagi segitiga OPQ,

\begin{array}{l} \tan 30^{\circ} = \frac{8}{Q P} \\ P Q = \frac{8}{\tan 30^{\circ}} = 13.86 cm \end{array}

∠QOR = 2(60^o) = 120^o

Sudut refleks ∠QOR = 360^o – 120^o = 240^o

240^{\circ} = \frac{3.142}{180^{\circ}} \times 240^{\circ} = 4.189 radian

Luas kawasan berlorek

= (Luas sektor SPT) – (Luas sector major OQR) – (Luas ∆ OPQ dan ∆ OPR)

= ½ (24)² (1.047) – ½ (8)² (4.189) – 2 (½ × 8 × 13.86)

= 301.54 – 134.05 – 110.88

= 56.61 cm²

Bab 8 Sukatan Membulat

Posted on May 27, 2016 by user

8.2 Panjang Lengkok Sesuatu Bulatan

(A) Rumus Panjang Lengkok dan Luas Bulatan

j = jejari, L= luas, s = panjang lengkok, θ = sudut dalam radian, l = panjang perentas

(B) Panjang Lengkok Sesuatu Bulatan

Contoh 1:

Suatu lengkok AB, yang berjejari 5 cm mencangkuk sudut 1.5 radian pada pusat bulatan.
Cari panjang lengkok AB.

Penyelesaian:

s = jθ

Panjang lengkok AB = (5)(1.5) = 7.5 cm

Contoh 2:

Suatu lengkok PQ, yang berjejari 12 cm mencangkuk sudut 30^opada pusat bulatan.
Cari panjang lengkok PQ.

Penyelesaian:

Panjang lengkok PQ

\begin{array}{l} = 12 \times 30^{\circ} \times \frac{π}{180^{\circ}} \\ = 6.283 cm \end{array}

Contoh 3:

Bagi rajah di atas, cari

(a) panjang lengkok minor AB

(b) panjang lengkok major APB

Penyelesaian:

(a)

panjang lengkok minor AB = jθ

= (7)(0.354)

= 2.478 cm

(b)

360^o = 2π radian, sudut refleks AOB

= (2π – 0.354) radian.

Panjang lengkok major APB

= 7 × (2π – 0.354)

= 7 × [(2)(3.1416) – 0.354]

= 7 × 5.9292

= 41.5044 cm

Bab 8 Sukatan Membulat

Posted on May 27, 2016 by user

8.3 Luas Sektor Sesuatu Bulatan

(A) Luas Sektor Sesuatu Bulatan

1. Jika sesuatu bulatan dibahagikan kepada dua sektor yang berlainan saiz, sektor yang lebih kecil dikenali sebagai sektor minor manakala sektor yang lebih besar dikenali sebagai sektor major.

2. Jika AOB ialah luas sektor suatu bulatan yang berjejari j, dan sudut θ radian yang tercangkum pada pusat bulatan O, maka

Contoh 1:

Dalam rajah di atas, cari luas sektor OAB.

Penyelesaian:

Luas sektor OAB

= ½ j²θ

= ½ (10)²(0.354)

= 17.7 cm²

(B) Mencari Luas Tembereng Sesuatu Bulatan

Contoh 2:

Rajah di atas menunjukkan sebuah sector bulatan yang berpusat O yang mempunyai jejari 6 cm.
Panjang lengkok AB ialah 8 cm. Cari

(i) ∠ AOB

(ii) luas tembereng berlorek.

Penyelesaian:

(i) Panjang lengkok AB = 8 cm

jθ = 8

6θ = 8

θ = 1.333 radian

∠AOB = 1.333 radian

(ii)

Luas tembereng berlorek

= ½ j² (θ – sinθ) (pastikan kalkulator dalam Mod Radian)

= ½ (6)² (1.333 – sin1.333)

= ½ (36) (1.333 – 0.972)

= 6.498 cm²

Bab 8 Sukatan Membulat

Posted on May 27, 2016 by user

Bab 8 Sukatan Membulat

8.1 Radian

(A) Takrifan Radian

(B) Menukar Ukuran dalam Darjah kepada Radian:

(C) Menukar Ukuran dalam Radian kepada Darjah:

Bab 10 Penyelesaian Segitiga

Posted on May 27, 2016 by user

10.4.2 Penyelesaian Segitiga, SPM Praktis (Kertas 2)

Soalan 2:

Rajah menunjukkan trapezium PQRS. PS adalah selari dengan QR dan ∠QRS ialah sudut cakah. Cari
(a) panjang, dalam cm, QS.
(b) panjang, dalam cm, RS.
(c) ∠QRS.
(d) luas, dalam cm², segitiga QRS.

Penyelesaian:

(a)

\begin{array}{l} \frac{Q S}{\sin P} = \frac{P S}{\sin Q} \\ \frac{Q S}{\sin 85^{\circ}} = \frac{13.1}{\sin 28^{\circ}} \\ Q S = \frac{13.1 \times \sin 85^{\circ}}{\sin 28^{\circ}} \\ Q S = 27.8 cm \end{array}

(b)

∠RQS = 180^o– 85^o – 28^o

∠RQS = 67^o

Guna petua kosinus,

RS² = QR²+ QS² – 2 (QR)(QS) kos ∠RQS

RS² = 6.4² + 27.8² – 2 (6.4)(27.8) kos 67^o

RS² = 813.8 – 139.04

RS² = 674.76

RS = 25.98 cm

(c)

Guna petua kosinus,

QS² = QR²+ RS² – 2 (QR)(RS) kos ∠RQS

27.8² = 6.4²+ 25.98² – 2 (6.4)(25.98) kos∠QRS

772.84 = 715.92 – 332.54 kos∠QRS

kos ∠ Q R S = \frac{715.92 - 772.84}{332.54}

kos∠QRS = –0.1712

∠QRS = 99.86^o

(d)

Luas segitiga QRS

= ½ (QR)(RS) sin R

= ½ (6.4) (25.98) sin 99.86^o

= 81.91 cm²