6.8.2 Statistik, SPM Praktis (Kertas 2)
Soalan 3:
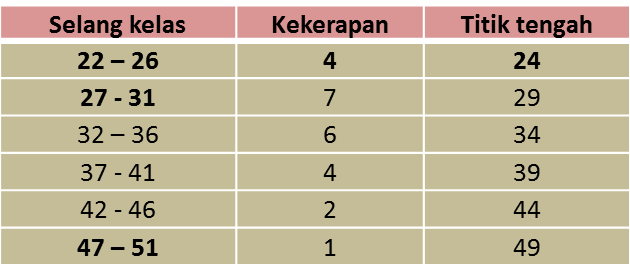
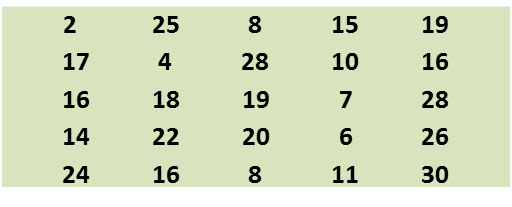
Data dalam rajah di bawah menunjukkan jisim, dalam kg, bagi 50 orang murid.
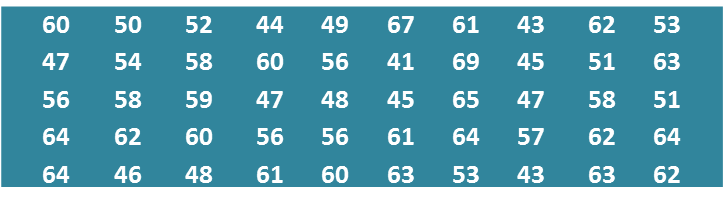
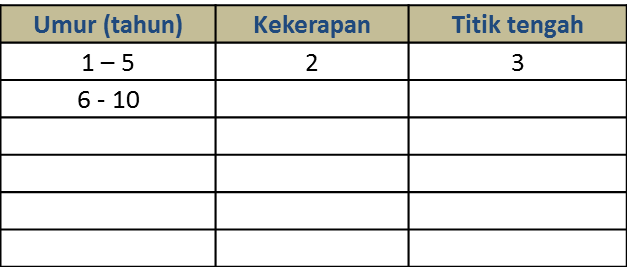
(a) Berdasarkan data dalam rajah, lengkapkan Jadual 2 di ruang jawapan.
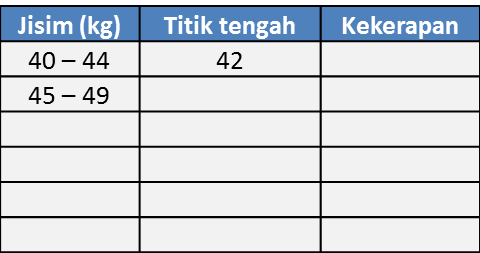 Jadual 2
Jadual 2(b) Berdasarkan Jadual 2,
(i) nyatakan saiz selang kelas yang digunakan dalam jadual 2.
(ii) hitung min anggaran jisim bagi murid itu.
Untuk ceraian soalan ini, gunakan kertas graf.
(c) Dengan menggunakan skala 2 cm kepada 5 kg pada paksi mengufuk dan 1 cm kepada 1 murid pada paksi mencancang, lukiskan satu poligon kekerapan bagi data tersebut.
Penyelesaian:
(a)
Jisim (kg) |
Titik tengah |
Kekerapan |
40 – 44 |
42 |
4 |
45 – 49 |
47 |
9 |
50 – 54 |
52 |
7 |
55 – 59 |
57 |
9 |
60 – 64 |
62 |
18 |
65 – 69 |
67 |
3 |
(b)(i)
saiz selang kelas
= Sempadan atas – sempadan bawah
= 44.5 – 39.5
= 5
(b)(ii)
Min anggaran jisim=42×4+47×9+52×7+57×9+62×18+67×350=278550=55.7
(c)
Soalan 4:
Rajah di bawah menunjukkan markah yang diperoleh sekumpulan 30 orang murid dalam suatu ujian Sains.
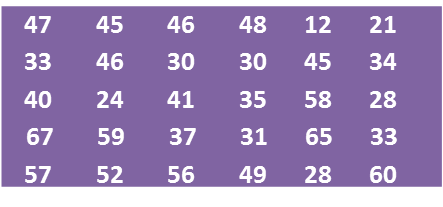
(a) Berdasarkan data pada Rajah di atas, lengkapkan Jadual di ruang jawapan.
(b) Berdasarkan Jadual lengkap di bahagian (a), hitung min anggaran markah bagi seorang murid.
Untuk ceraian soalan ini, gunakan kertas graf.
(c) Dengan menggunakan skala 2 cm kepada 10 markah pada paksi mengufuk dan 2 cm kepada 1 murid pada paksi mencancang, lukiskan satu poligon kekerapan bagi data tersebut.
(d) Markah lulus ujian itu ialah 44. Menggunakan poligon kekerapan di bahagian (c), nyatakan bilangan murid yang lulus di dalam ujian itu.
Jawapan:
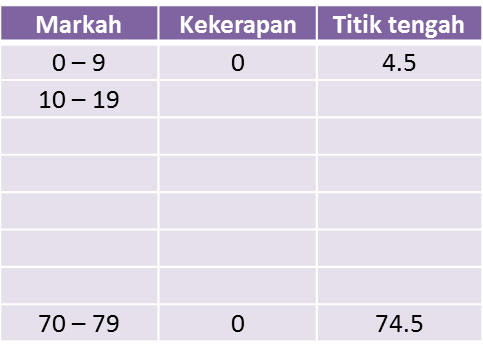
Penyelesaian:
(a)
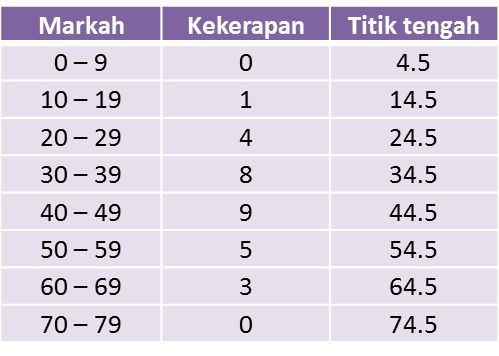
(b)
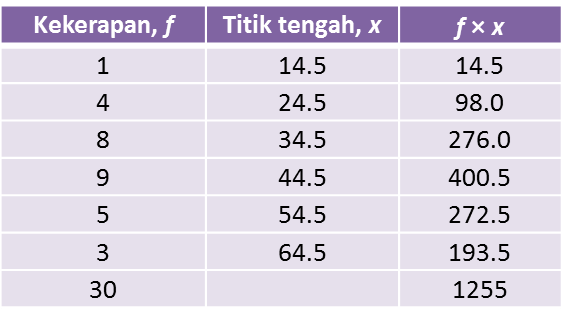
Min anggaran markah = 125530 = 41.83
(c)
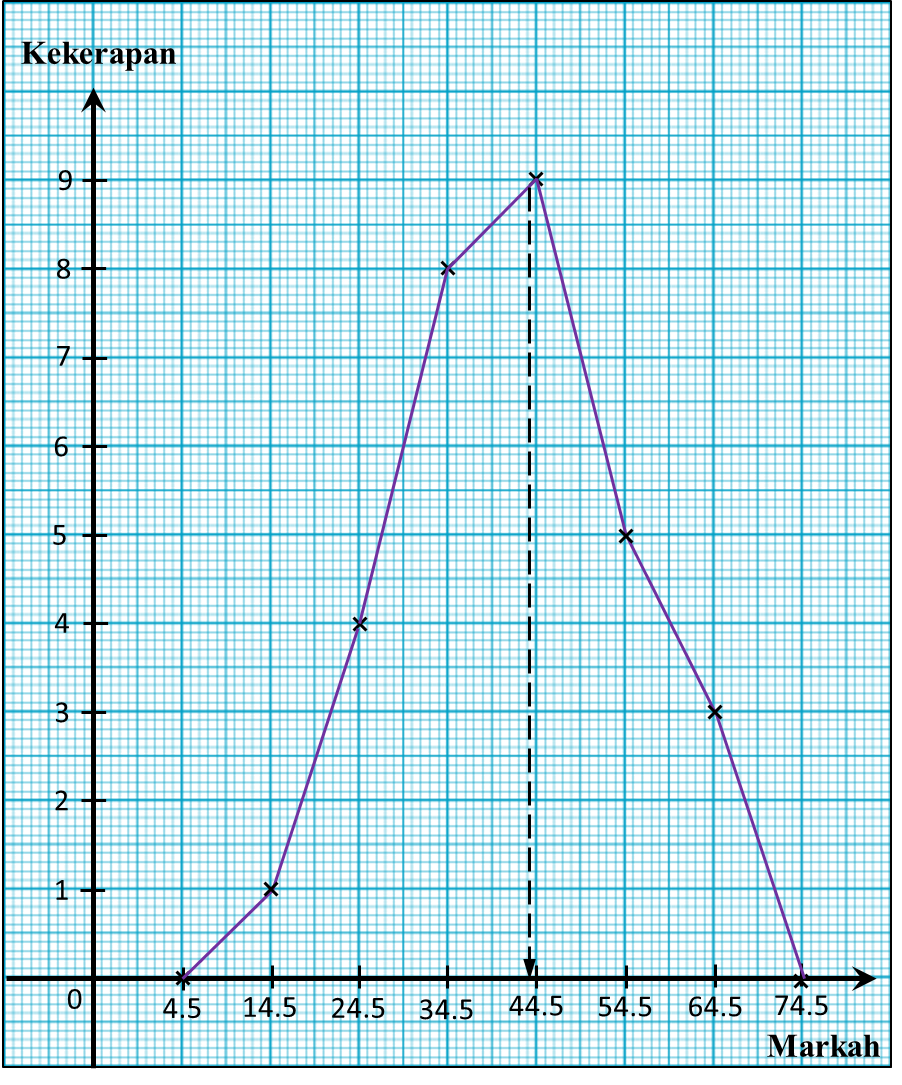
(d)
Number of students who passed the test
= 9 + 5 + 3
= 17
Rajah di bawah menunjukkan markah yang diperoleh sekumpulan 30 orang murid dalam suatu ujian Sains.

(a) Berdasarkan data pada Rajah di atas, lengkapkan Jadual di ruang jawapan.
(b) Berdasarkan Jadual lengkap di bahagian (a), hitung min anggaran markah bagi seorang murid.
Untuk ceraian soalan ini, gunakan kertas graf.
(c) Dengan menggunakan skala 2 cm kepada 10 markah pada paksi mengufuk dan 2 cm kepada 1 murid pada paksi mencancang, lukiskan satu poligon kekerapan bagi data tersebut.
(d) Markah lulus ujian itu ialah 44. Menggunakan poligon kekerapan di bahagian (c), nyatakan bilangan murid yang lulus di dalam ujian itu.
Jawapan:

Penyelesaian:
(a)

(b)

Min anggaran markah = 125530 = 41.83
(c)

(d)
Number of students who passed the test
= 9 + 5 + 3
= 17
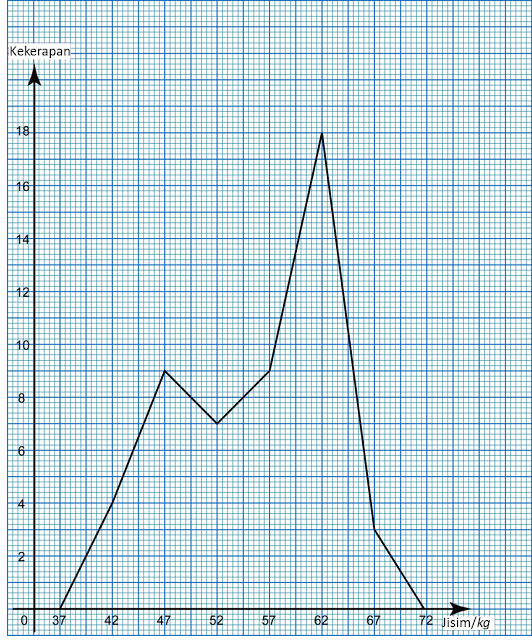
 Jadual 1
Jadual 1
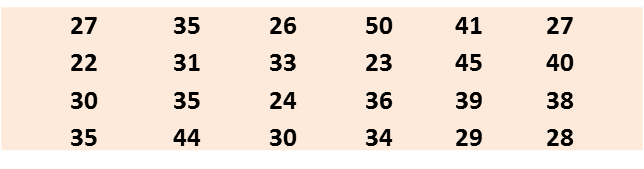 (a) Berdasarkan data di rajah di atas, lengkapkan Jadual di ruang jawapan.
(a) Berdasarkan data di rajah di atas, lengkapkan Jadual di ruang jawapan.