Bab 20 Bumi sebagai Sfera

Posted on June 27, 2016 by user

9.6.1 Bumi Sebagai Sfera, SPM Praktis (Kertas 2)

Soalan 1:

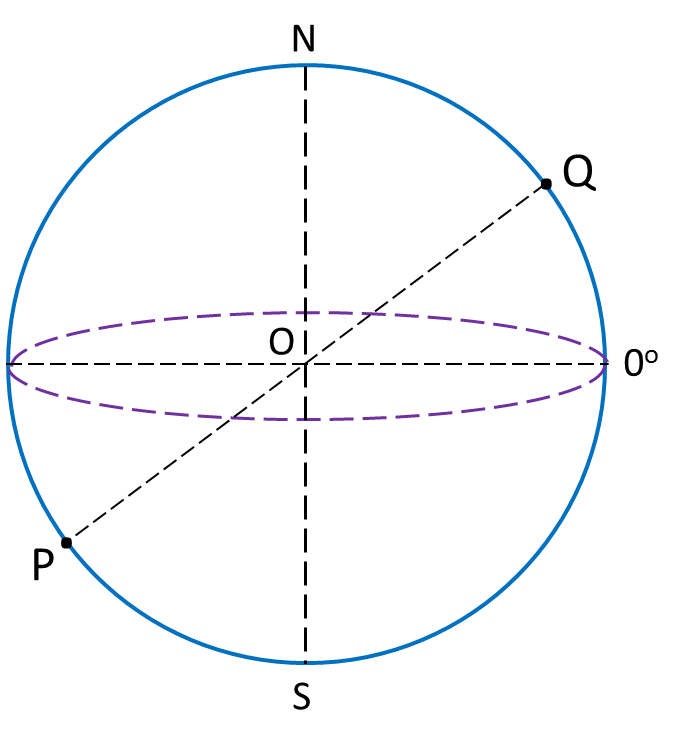
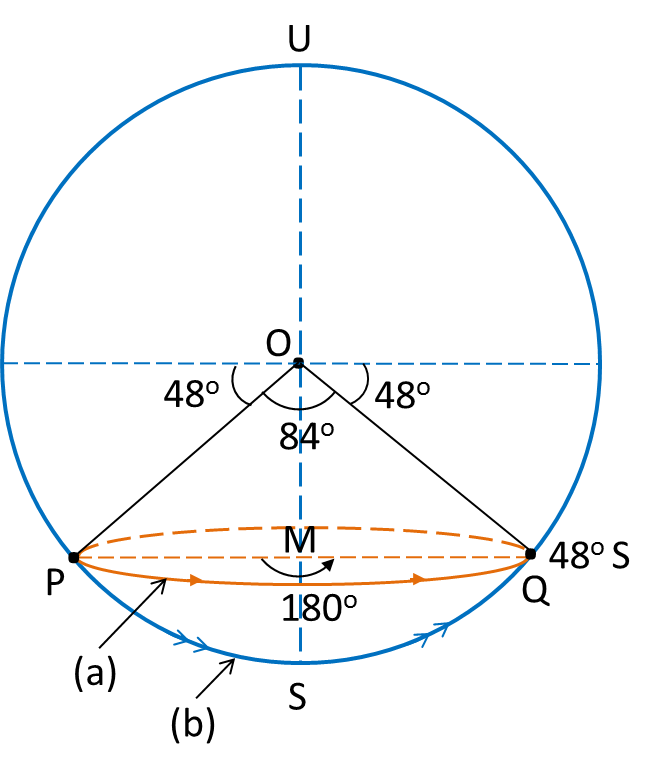
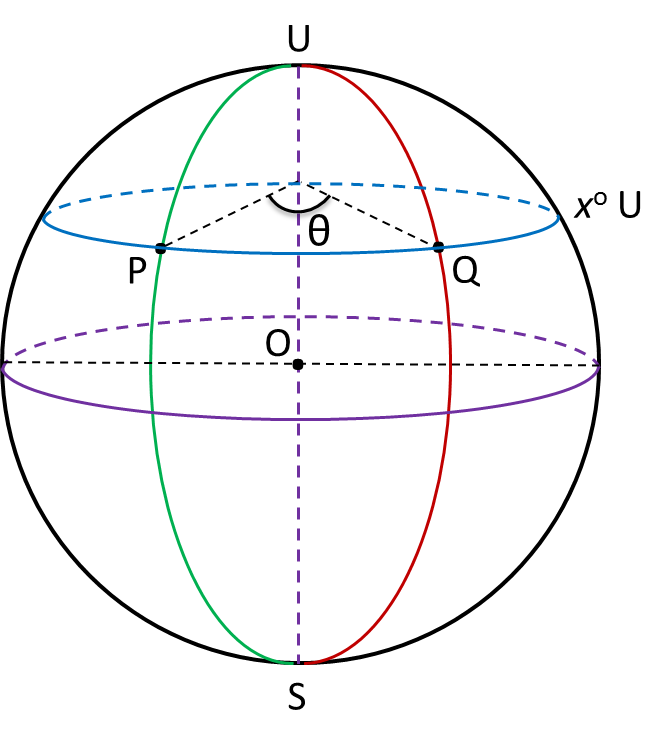
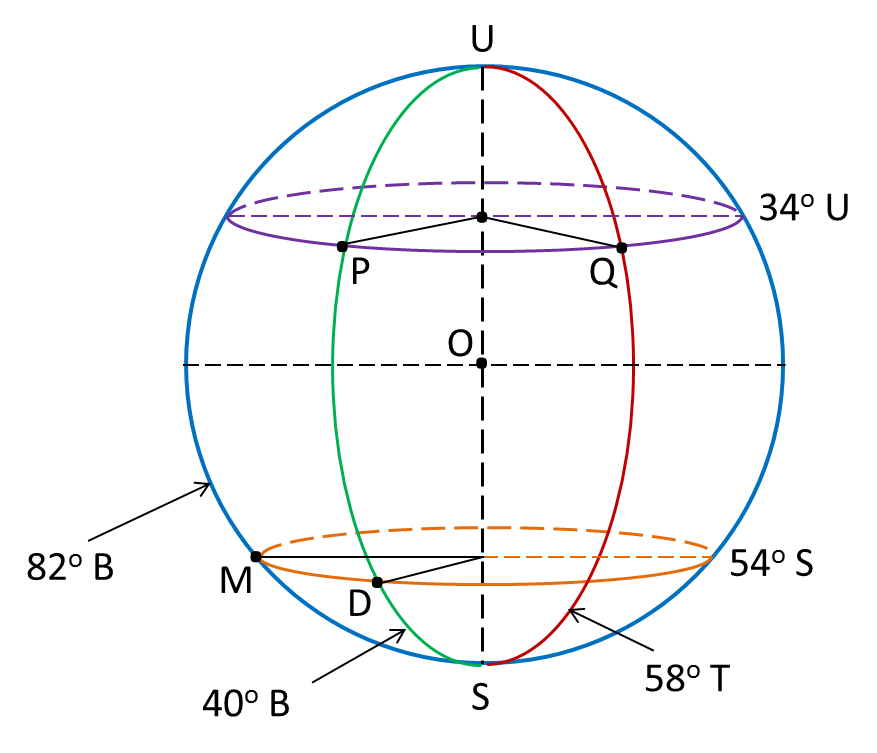
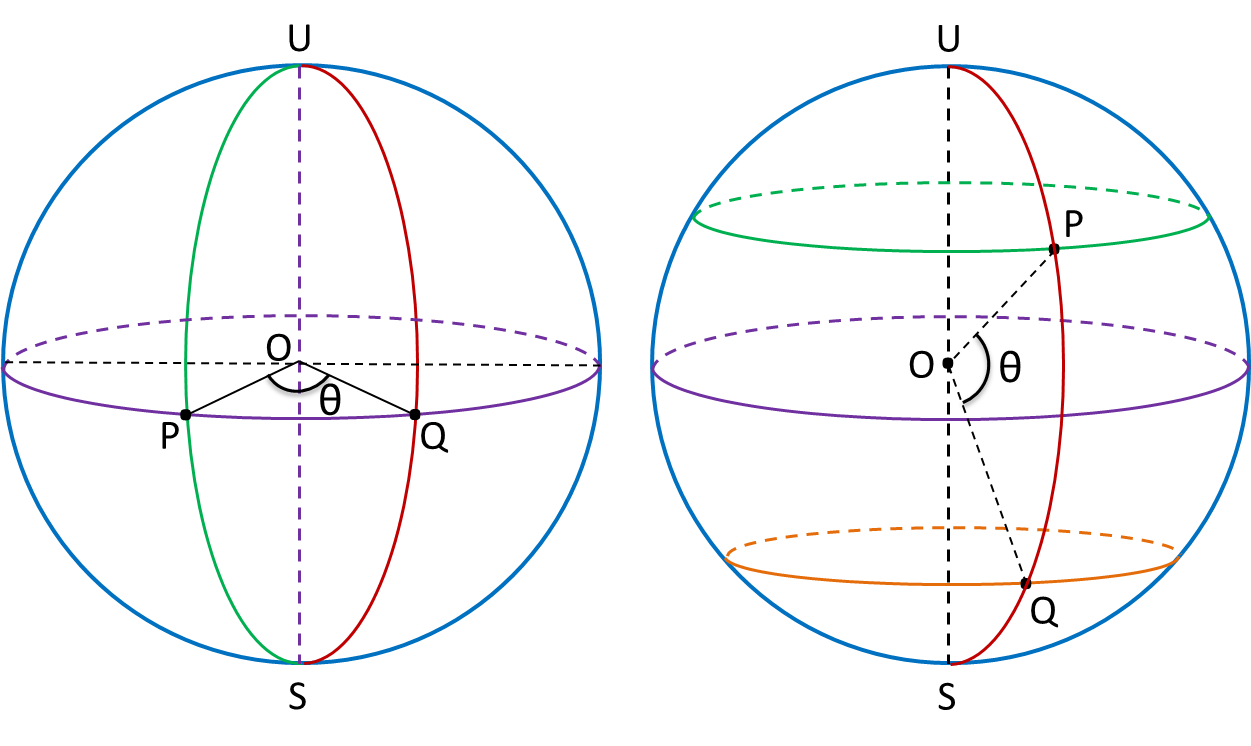
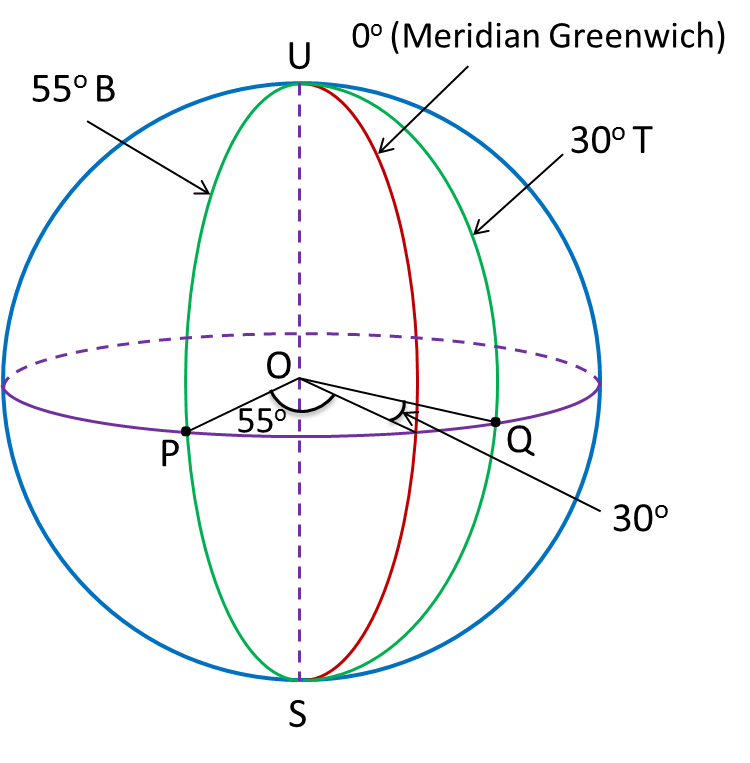
Rajah di bawah menunjukkan empat titik P, Q, R dan M, di permukaan bumi. P terletak pada longitud 70^oB. QR ialah diameter selarian latitud 40^oU. M terletak 5700 batu nautika ke selatan P.

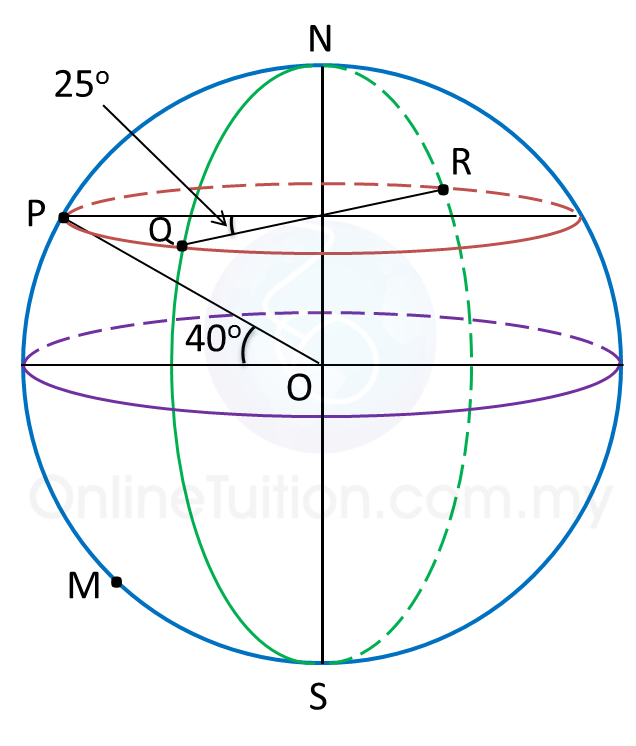
(a) Cari kedudukan bagi R.

(b) Hitungkan jarak terpendek, dalam batu nautika, dari Q ke R, diukur sepanjang permukaan bumi.

(d) Sebuah kapal terbang berlepas dari R arah ke barah ke P mengikut selarian latitud sepunya dengan purata laju 660 knot.

Hitung masa, dalam jam, penerbangan itu.

Penyelesaian:

(a)

Latitud R = latitud Q = 40^o U

Longitud bagi Q = (70^o – 25^o) B = 45^o B

Longitud bagi R = (180^o – 45^o) T = 135^o T

Oleh itu, kedudukan bagi R = (40^o U, 135^oT).

(b)

Jarak terpendek dari Q ke R

= (180 – 40 – 40) x 60

= 100 × 60

= 6000 batu nautika

(c)

\begin{array}{l} ∠ P O M = \frac{5700}{60} \\ = 95^{o} \\ ∴ Latitud bagi M = (95^{o} - 40^{o}) S \\ = 55^{o} S \end{array}

(d)

\begin{array}{l} Masa = \frac{jarak dari R ke P}{purata laju} \\ = \frac{(180 - 25) \times 60 \times k o s 40^{o}}{660} \\ = \frac{155 \times 60 \times k o s 40^{o}}{660} \\ = 10.79 jam \end{array}

Bab 20 Bumi sebagai Sfera

Posted on June 27, 2016 by user

9.5 Bumi Sebagai Sfera, SPM Praktis (Kertas 1)

Soalan 1:

Dalam rajah di bawah, U ialah Kutub Utara dan S ialah Kutub Selatan. Kedudukan titik P ialah (40^o S, 70^o B) dan POQ ialah diameter bumi.

Cari Longitud bagi Q.

Penyelesaian:

Sejak PQ ialah diameter bumi dan longitud bagi P ialah θ^o B, longitud bagi Q ialah (180^o – θ^o) T.

Longitud bagi P = 70^o B

Longitud bagi Q = (180^o – 70^o) T

= 110^oT

Soalan 2:

Dalam rajah di bawah, U ialah Kutub Utara dan S ialah Kutub Selatan dan NOS ialah paksi bumi.

Cari kedudukan titik Q.

Penyelesaian:

Latitud bagi Q = (90^o – 42^o) U

= 48^o U

Longitud bagi Q = (65^o – 30^o) T

= 35^o T

Oleh itu, kedudukan titik Q = (48^o U, 30^oT).

Bab 20 Bumi sebagai Sfera

Posted on June 27, 2016 by user

9.4.3 Jarak Terpendek di antara Dua Titik

1. Jarak terpendek di antara dua titik adalah di sepanjang longitud atau bulatan agong.

Jarak terpendek antara titik D dan titik M

= ( θ × 60 ) batu nautika

Contoh:

Dalam rajah di atas, hitung

(a) jarak dari P ke Q, diukur sepanjang selarian latitud 48^o S,

(b) jarak dari P ke Q, diukur sepanjang laluan PSQ, dan S ialah kutub selatan.

Nyatakan jarak terpendek.

Penyelesaian:

(a)

Jarak dari P ke Q, diukur sepanjang selarian latitud 48^o S

= 180 × 60 × kos 48^o ← (sudut PMQ = 180^o)

= 7266.61 b.n.

(b)

Jarak dari P ke Q, diukur sepanjang laluan PSQ, dan S ialah kutub selatan

= 84 × 60 ← (sudut POQ = 180^o – 48^o – 48^o= 84^o)

= 5040 b.n.

Jarak dari P ke Q, diukur sepanjang laluan PSQ dalam (b), dan S ialah kutub selatan, adalah lebih pendek berbanding dengan jarak dalam (a).

Jarak terpendek dalam contoh di atas ialah

Jarak diukur di sepanjang bulatan agung yang

melalui Kutub Selatan (atau Utara).

Bab 20 Bumi sebagai Sfera

Posted on June 27, 2016 by user

9.4.2 Jarak di antara Dua Titik pada Selarian Latitud yang Sama

1. Untuk mencari jarak di sepanjang selarian latitud yang sama:

Jarak di antara titik P dan titik Q

= ( beza di antara dua longitud itu dalam minit ) × kos latitud

= ( θ × 60 × kos x^o ) batu nautika

Contoh:

Dalam rajah di atas, hitung

(a) jarak PQ, diukur sepanjang selarian latitud 34^o U,

(b) jarak DM, diukur sepanjang selarian latitud 54^o S.

Penyelesaian:

(a)

Beza di antara dua longitud P dan Q

= 40^o+ 58^o= 98^o

Oleh itu, jarak PQ, diukur sepanjang selarian latitud 34^o U

= 98 × 60 × kos 34^o← [θ × 60 × kos (latitud)]

= 4874.74 b.n.

(b)

Beza di antara dua longitud D dan M

= 82^o– 40^o= 42^o

Oleh itu, jarak DM, diukur sepanjang selarian latitud 54^o S

= 42 × 60 × kos 54^o← [θ × 60 × kos (latitud)]

= 1481.22 b.n.

Bab 20 Bumi sebagai Sfera

Posted on June 27, 2016 by user

9.4 Jarak Pada Permukaan Bumi

9.4.1 Jarak di antara dua titik diukur sepanjang bulatan agung

1. Satu batu nautika (b.n.) ialah panjang lengkok bulatan agung yang mencangkum sudut satu minit di pusat bumi.

2. Jarak di antara dua titik pada permukaan bumi ialah panjang lengkok bulatan yang menghubungkan kedua-dua titik itu di sepanjang permukaan bumi.

3. Untuk mencari jarak di antara dua titik di sepanjang meridian atau Khatulistiwa:

Jarak di antara P dan Q

= ( θ × 60 ) batu nautika

Bab 20 Bumi sebagai Sfera

Posted on June 27, 2016 by user

9.3 Kedudukan Tempat

Kedudukan sesuatu tempat pada permukaan bumi ditentukan oleh latitud dan longitudnya dan ditulis sebagai (x^o U/S, y^o T/B) ← (latitud, longitud).

Contoh:

Kedudukan tempat bagi titik P ialah (35^o U, 27^o T).

Bab 20 Bumi sebagai Sfera

Posted on June 27, 2016 by user

9.2 Latitud

1. Bulatan agong yang satahnya berserenjang dengan paksi bumi dikenali sebagai Khatulistiwa.

2. Bulatan yang satahnya berserenjang dengan paksi bumi dan selari dengan satah khatulistiwa dikenali sebagai selarian latitud.

3. Latitud ialah sudut pada pusat bumi yang dicangkum oleh lengkok suatu meridian bermula dari Khatulistiwa ke selarian latitud.

4. Latitud Khatulistiwa ialah 0^o.

5. Semua titik pada selarian latitud yang sama mempunyai latitud yang sama.

Contoh:

Latitud bagi D ialah 30^o U.

Latitud bagi E ialah 45^o S.

Beza di antara Dua Latitud

1. Jika kedua-dua selarian latitud berada ke utara atau ke selatan Khatulistiwa, menolakkan sudut-sudut latitud mereka untuk mencari beza antara dua latitud.

2. Jika satu selarian latitud berada ke utara Khatulistiwa dan satu selarian latitud yang lain berada ke selatan Khatulistiwa, menambahkan sudut-sudut latitud mereka untuk mencari beza antara dua latitud.

Bab 20 Bumi sebagai Sfera

Posted on June 27, 2016 by user

9.1 Longitud

1. Bulatan agung ialah bulatan yang terbentuk pada permukaan bumi oleh suatu satah yang melalui pusat bumi.

2. Meridian adalah separuh bulatan agung yangmenyambungkan Kutub Utara dan Kutub Selatan.

3. Meridian yang melalui bandar Greenwich di England disebut Meridian Greenwich

4. Longitud bagi Meridian Greenwich adalah 0^o.

5. Longitud sesuatu meridian ditentukan oleh:

(a) sudut di antara satah meridian itu dengan satah Meridian Greenwich.

(b) Kedudukan meridian itu ke timur atau ke barat Meridian Greenwich.

Contoh:

Longitud bagi P ialah 55^o B.

Longitud bagi Q ialah 30^o T.

6. Semua titik yang terletak pada meridian yang saman mempunyai longitud yang sama.

Beza di antara Dua longitud

1. Jika kedua-dua longitud berada ke barat atau ke timur Meridian Greenwich, menolakkan sudut-sudut longitud mereka untuk mencari beza antara dua longitud.

2. Jika satu longitud berada ke barat Meridian Greenwich dan longitud yang lain berada ke timur Meridian Greenwich, menambahkan sudut-sudut longitud mereka untuk mencari beza antara dua longitud.

Bab 18 Kebarangkalian II

Posted on June 25, 2016 by user

7.3 Kebarangkalian Peristiwa Bergabung

7.3b Mencari Kebarangkalian Peristiwa Bergabung (a) Aatau B (b) A dan B

1. Rumus yang berikut digunakan untuk mencari kebarangkalian peristiwa bergabung ‘A atau B’.

\begin{array}{l} P (A atau B) = P (A \cup B) \\ = \frac{n (A \cup B)}{n (S)} \end{array}

2. Rumus yang berikut pula digunakan untuk mencari kebarangkalian peristiwa bergabung ‘A dan B’.

\begin{array}{l} P (A dan B) = P (A \cap B) \\ = \frac{n (A \cap B)}{n (S)} \end{array}

Contoh:

Kebarangkalian bahawa dua pelajar tingkatan 5, Farhana dan Wendy akan lulus ujian lisan Bahasa Inggeris ialah

\frac{1}{3} dan \frac{2}{5}

masing-masing. Hitung kebarangkalian bahawa

(a) kedua-dua Farhana dan Wendy lulus ujian lisan Bahasa Inggeris,

(b) kedua-dua Farhana dan Wendy gagal ujian lisan Bahasa Inggeris,

(c) salah seorang daripada mereka lulus ujian lisan Bahasa Inggeris,

(d) sekurang-kurangnya salah seorang daripada mereka lulus ujian lisan Bahasa Inggeris.

Penyelesaian:

Katakan

F = Peristiwa bahawa Farhana lulus ujian lisan Bahasa Inggeris

W = Peristiwa bahawa Wendy lulus ujian lisan Bahasa Inggeris

Oleh itu,

F’ = Peristiwa bahawa Farhana gagal ujian lisan Bahasa Inggeris

W’ = Peristiwa bahawa Wendy gagal ujian lisan Bahasa Inggeris

\begin{array}{l} P (F) = \frac{1}{3}, P (F') = \frac{2}{3} \\ P (W) = \frac{2}{5}, P (W') = \frac{3}{5} \end{array}

(a)

P (kedua-dua Farhana dan Wendy lulus ujian lisan Bahasa Inggeris)

= P (F ∩ W)

= P (F) × P (W)

\begin{array}{l} = \frac{1}{3} \times \frac{2}{5} \\ = \frac{2}{15} \end{array}

(b)

P (kedua-dua Farhana dan Wendy gagal ujian lisan Bahasa Inggeris)

= P (F’ ∩ W’)

= P (F’) × P (W’)

\begin{array}{l} = \frac{2}{3} \times \frac{3}{5} \\ = \frac{2}{5} \end{array}

(c)

P (salah seorang daripada mereka lulus ujian lisan Bahasa Inggeris)

= P (F ∩ W’) + P (F’ ∩ W)

= (P (F) × P (W’)) + (P (F’) × P (W))

\begin{array}{l} = (\frac{1}{3} \times \frac{3}{5}) + (\frac{2}{3} \times \frac{2}{5}) \\ = \frac{7}{15} \end{array}

(d)

P (sekurang-kurangnya salah seorang daripada mereka lulus ujian lisan Bahasa Inggeris)

= 1 – P (kedua-duanya gagal) ← (Konsep peristiwa pelengkap)

= 1 – P (F’) × P (W’)

\begin{array}{l} = 1 - \frac{2}{5} \\ = \frac{3}{5} \end{array}

Bab 18 Kebarangkalian II

Posted on June 25, 2016 by user

7.5 Kebarangkalian II, SPM Praktis (Kertas 2)

Soalan 1:

Tiga belas keping kad huruf seperti yang ditunjukkan dalam rajah di atas dimasukkan ke dalam sebuah kotak.

Dua keping kad dikeluarkan secara rawak daripada kotak itu, satu demi satu, tanpa pengembalian. Hitung kebarangkalian bahawa

(a) kad pertama yang dikeluarkan ialah kad huruf Ndan kad kedua yang dikeluarkan ialah kad huruf I.

(b) dua keping kad yang dikeluarkan adalah kad yang sama huruf.

Penyelesaian:

(a)

Terdapat 3 keping kad dengan huruf ‘N’ dan 1 keping kad huruf ‘I’.

P (kad pertama yang dikeluarkan ialah kad huruf Ndan kad kedua yang dikeluarkan ialah kad huruf I)

\begin{array}{l} = \frac{3}{13} \times \frac{2}{(13 - 1)} \\ = \frac{3}{13} \times \frac{2}{12} = \frac{1}{26} \end{array}

(b)

P (dua keping kad yang dikeluarkan adalah kad yang sama huruf)

= P (II or NN or TT or AA)

= P (II) + P (NN) + P (TT) + P (AA)

\begin{array}{l} = (\frac{2}{13} \times \frac{1}{12}) + (\frac{3}{13} \times \frac{2}{12}) + (\frac{2}{13} \times \frac{1}{12}) + (\frac{2}{13} \times \frac{1}{12}) \\ ↑ \\ Terdapat 3 huruf ' N' \\ = \frac{2}{156} + \frac{6}{156} + \frac{2}{156} + \frac{2}{156} \\ = \frac{12}{156} \\ = \frac{1}{13} \end{array}

Soalan 2:

Sempena Hari Kebangsaan, sekumpulan pelajar yang terdiri daripada 8 pelajar lelaki dan 5 orang pelajar perempuan mengambil bahagian dalam pertandingan nyanyian. Setiap hari, dua orang pelajar dipilih secara rawak daripada kumpulan pelajar itu untuk membuat persembahan khas.

(a) Hitung kebarangkalian bahawa kedua-dua pelajar yang dipilih untuk membuat persembahan khas itu adalah lelaki.

(b) Dua orang pelajar lelaki yang telah membuat persembahan khas itu dikecualikan daripada membuat persembahan khas pada hari kedua.

Hitung kebarangkalian bahawa dua orang pelajar yang dipilih untuk membuat persembahan khas dalam hari kedua terdiri daripada jantina yang sama.

Penyelesaian:

(a)

P (kedua-dua orang pelajar adalah lelaki)

= P (LL)

\begin{array}{l} = \frac{8}{13} \times \frac{7}{12} \\ = \frac{7}{24} \end{array}

(b)

P (kedua-dua orang pelajar adalah daripada jantina yang sama)

= P (LL) + P (PP)

\begin{array}{l} = (\frac{6}{11} \times \frac{5}{10}) + (\frac{5}{11} \times \frac{4}{10}) \leftarrow \begin{array}{l} 11 orang pelajar tinggal dalam \\ kumpulan dalam hari kedua selepas \\ dua orang pelajar lelaki dikecualikan . \end{array} \\ = \frac{3}{11} + \frac{2}{11} \\ = \frac{5}{11} \end{array}