Bab 11 Nombor Indeks

Posted on July 7, 2016 by user

11.3.1 Nombor Indeks, SPM Praktis (Kertas 2)

Soalan 1:

Jadual di bawah menunjukkan indeks harga dan peratus penggunaan bagi empat bahan , P, Q, R dan S, yang meruapakan bahan utama dalam pengeluaran suatu jenis barang mainan.

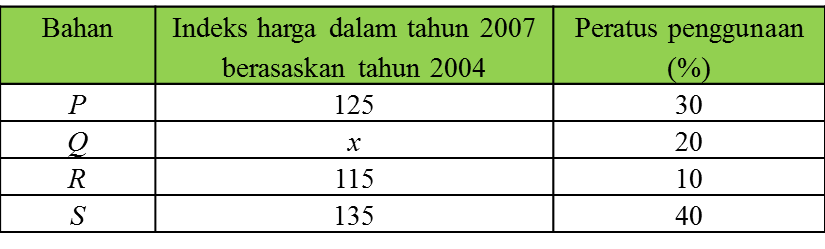
(a) Hitung

(i) harga bahan S pada tahun 2004 jika harganya pada tahun 2007 ialah RM43.20,

(ii) indeks harga P pada tahun 2007 berasaskan tahun 2002 jika indeks harga pada tahun 2004 berasaskan tahun 2002 ialah 110.

(b) Indeks gubahan bagi kos pengeluaran barang mainan itu pada tahun 2007 berasaskan tahun 2004 ialah 125.

Hitung

(i) nilai x ,

(ii) harga bagi barang mainan itu pada tahun 2004 jika harga yang sepadan pada tahun 2007 ialah RM75.

Penyelesaian:

(a)(i)

\begin{array}{l} 135 = \frac{43.2}{P_{2004}} \times 100 \\ P_{2004} = \frac{43.2 \times 100}{135} = 32 \end{array}

Maka, harga bahan S pada tahun 2004 ialah RM32.

(a)(ii)

\begin{array}{l} Diberi \frac{P_{2004}}{P_{2002}} \times 100 = 110 \to \frac{P_{2004}}{P_{2002}} = \frac{110}{100} \\ dan \frac{P_{2007}}{P_{2004}} \times 100 = 125 \to \frac{P_{2007}}{P_{2004}} = \frac{125}{100} \end{array}

Indeks harga P pada tahun 2007 berasaskan tahun 2002,

\begin{array}{l} I = \frac{P_{2007}}{P_{2002}} \times 100 \\ I = \frac{P_{2007}}{P_{2004}} \times \frac{P_{2004}}{P_{2002}} \times 100 \\ I = \frac{125}{100} \times \frac{110}{100} \times 100 \\ I = 137.50 \end{array}

(b)(i)

\begin{array}{l} Diberi indeks gubahan \bar{I} = 125 \\ \bar{I} = \frac{\sum I W}{\sum W} \\ 125 = \frac{(125) (30) + (x) (20) + (115) (10) + (135) (40)}{30 + 20 + 10 + 40} \\ 125 = \frac{10300 + 20 x}{100} \\ 12500 = 10300 + 20 x \\ x = 110 \end{array}

(b)(ii)

Katakan harga bagi barang mainan itu pada tahun 2004 ialah P₂₀₀₄

\begin{array}{l} P_{2004} \times \frac{125}{100} = 75 \\ P_{2004} = R M 60 \end{array}

Bab 6 Geometri Koordinat

Posted on July 7, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 6:

Penyelesaian secara lukisan berskala tidak akan diterima.

Rajah di bawah menunjukkan sebuah segi tiga OPQ. Titik S terletak pada garis PQ.

(a) Suatu titik Y bergerak dengan keadaan jaraknya dari titik S adalah sentiasa 5 uint.

Cari persamaan lokus Y.

(b) Diberi bahawa titik P dan titik Q terletak pada lokus Y.

Hitung

(i) nilai k,

(ii) koordinat Q.

(c) Seterusnya, cari luas, dalam uint², bagi segi tiga OPQ.

Penyelesaian:

(a)

Katakan koordinat titik Yialah (x, y), dan YS = 5 unit

\sqrt{{(x - 5)}^{2} + {(y - 3)}^{2}} = 5

x² – 10x + 25 + y² – 6y + 9 = 25

x² + y² – 10x – 6y + 9 = 0

(b)(i)

Diberi titik P (2,k) terletak pada lokus Y

(2)² + (k)²– 10 (2) – 6 (k) + 9 = 0

4 + k² – 20 – 6k + 9 = 0

k² – 6k – 7 = 0

(k – 7) (k + 1) = 0

k = 7 atau k = –1

Berdasarkan rajah, k = 7

(b)(ii)

Diberi P dan Q terletak pada lokus Y, Sialah titik tengah PQ. P = (2, 7), S = (5, 3)

Katakan koordinat Q = (x, y),

\begin{array}{l} (\frac{2 + x}{2}, \frac{7 + y}{2}) = (5, 3) \\ \frac{2 + x}{2} = 5 dan \frac{7 + y}{2} = 3 \end{array}

2 + x = 10 dan 7 + y= 6

x = 8 dan y = –1

Koordinat Q = (8, –1).

(c)

Luas ∆ OPQ

\begin{array}{l} = \frac{1}{2} | \begin{array}{l} 0 8     2 \\ 0 - 17 \end{array} \begin{array}{l} 0 \\ 0 \end{array} | \\ = \frac{1}{2} | 0 + (8) (7) + 0 - 0 - (- 1) (2) - 0 | \\ = \frac{1}{2} | 58 | \\ = 29 {unit}^{2} \end{array}

Bab 6 Geometri Koordinat

Posted on July 7, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 5:

Dalam rajah di atas, persamaan bagi garis lurus FMG ialah y = – 4. Satu titik P bergerak dengan keadaan jaraknya dari E adalah sentiasa separah jarak bagi E dari garis lurus FG. Cari

(a) persamaan bagi lokus P,

(b) koordinat-xbagi titik persilangan antara lokus dengan paksi-x.

Penyelesaian:

( a)

Kecerunan garis lurus FMG= 0

EM iadalah berserenjang dengan FMG, jadi kecerunan EM adalah juga = 0, persamaan EM adalah x = 2

Koordinat bagi titik M= (2, –4).

Katakan koordinat bagi titik P = (x, y).

Diberi PE = ½ EM

2PE = EM

2 \sqrt{{(x - 2)}^{2} + {(y - 4)}^{2}} = \sqrt{{(2 - 2)}^{2} + {(4 - (- 4))}^{2}}

4 (x²– 4x + 4 + y² – 8y +16) = (0 + 64) → (Kuasa duakan kedua-dua belah)

4x²– 16x + 16 + 4y² – 32y + 64 = 64

4x²+ 4y² – 16x – 32y + 16 = 0

x² + y² – 4x – 8y + 4 = 0

( b)

x² + y² – 4x – 8y + 4 = 0

pada paksi-x, y = 0.

x² + 0 – 4x – 8(0) + 4 = 0

x² – 4x+ 4 = 0

(x – 2) (x – 2) = 0

x = 2

Jadi, koordinat-x bagi titik persilangan antara lokus dengan paksi-x ialah 2.

Bab 6 Geometri Koordinat

Posted on July 7, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 4:

Rajah di atas menunjukkan segitiga LMN dengan keadaan L terletak di paksi-y. Persamaan garis lurus LKN dan MK adalah 2y – 3x + 6 = 0 dan 3y + x – 13 = 0 masing-masing. Cari

(a) koordinat titik K

(b) nisbah LK:KN

Penyelesaian:

(a)

2y – 3x + 6 = 0 ----(1)

3y + x – 13 = 0 ----(2)

x = 13 – 3y ----(3)

Gantikan persamaan (3) ke dalam (1),

2y – 3 (13 – 3y) + 6 = 0

2y – 39 + 9y + 6 = 0

11y = 33

y = 3

Gantikan y = 3 ke dalam persamaan (3),

x = 13 – 3 (3)

x = 4

Koordinat titik K = (4, 3).

(b)

Diberi persamaan LKNialah 2y – 3x + 6 = 0

Di paksi-y, x = 0,

2y – 3(0) + 6 = 0

2y = –6

y = –3

koordinat titik L= (0, –3).

Nisbah LK:KN

Samakan koordinat x,

\begin{array}{l} \frac{L K (10) + K N (0)}{L K + K N} = 4 \\ 10 L K = 4 L K + 4 K N \\ 6 L K = 4 K N \\ \frac{L K}{K N} = \frac{4}{6} \\ \frac{L K}{K N} = \frac{2}{3} \end{array}

Nisbah LK:KN = 2 : 3

Bab 6 Geometri Koordinat

Posted on July 7, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 3:

Dalam rajah di atas, PRS dan QRT ialah garis lurus. Diberi Radalah titik tengah bagi PS dan QR : RT = 1 : 3, Cari

(a) koordinat titik R,

(b) koordinat titik T,

(c) koordinat bagi titik persilangan antara garis PQ dan garis ST.

Penyelesaian:

(a)

Diberi R ialah titik tengah bagi PS.

\begin{array}{l} R = (\frac{3 + 7}{2}, \frac{2 + 6}{2}) \\ R = (5, 4) \end{array}

(b)

QR : RT = 1 : 3

Katakan koordinat titik T = (x, y)

\begin{array}{l} (\frac{(1) (x) + (3) (4)}{1 + 3}, \frac{(1) (y) + (3) (5)}{1 + 3}) = (5, 4) \\ \frac{x + 12}{4} = 5 \\ x + 12 = 20 \\ x = 8 \\ \frac{y + 15}{4} = 4 \end{array}

y + 15 = 16

y = 1

T = (8, 1)

(c)

Kecerunan P Q = \frac{5 - 2}{4 - 3} = 3

Persamaan PQ,

y – 2 = 3 (x – 3)

y – 2 = 3x – 9

y = 3x – 7 ---- (1)

Kecerunan S T = \frac{6 - 1}{7 - 8} = - 5

Persamaan ST,

y – 1 = –5 (x – 8)

y – 1 = –5x + 40

y = –5x + 41 ---- (2)

Gantikan (1) ke dalam (2),

3x – 7 = –5x + 41

8x = 48

x = 6

Dari (1),

y = 3(6) – 7 = 11

Koordinat bagi titik persilangan antara garis PQ dan garis ST = (6, 11).

Bab 6 Geometri Koordinat

Posted on July 7, 2016 by user

6.7 Geometri Koordinat, SPM Praktis (Kertas 1)

Soalan 6:

Titik M ialah (-3, 5) dan titik N ialah (4, 7). Titik P bergerak dengan keadaan PM: PN= 2: 3. Cari persamaan lokus bagi P.

Penyelesaian:

Katakan P = (x, y)

PM : PN = 2 : 3

\begin{array}{l} \frac{P M}{P N} = \frac{2}{3} \\ 3 P M = 2 P N \\ 3 \sqrt{{(x - (- 3))}^{2} + {(y - 5)}^{2}} = 2 \sqrt{{(x - 4)}^{2} + {(y - 7)}^{2}} \end{array}

Menguasa dua kedua-dua belah untuk menghapuskan punca kuasa dua.

9[x²+ 6x + 9 + y² – 10y + 25] = 4 [x² – 8x + 16 + y² – 14y + 49]

9x²+ 54x + 9y² – 90y + 306 = 4x² – 32x + 4y²– 56y + 260

5x²+ 5y² + 86x – 34y + 46 = 0

Oleh itu, persamaan lokus bagi titik P ialah

5x² + 5y² + 86x – 34y + 46 = 0

Soalan 7:

Diberi titik A (0,2) dan titik B (6,5). Cari persamaan lokus bagi suatu titik bergerak P dengan keadaan APB sentiasa bersudut tegak di P.

Penyelesaian:

Katakan P = (x, y)

Diberi segi tiga APB = 90^o, maka AP adalah berserenjang dengan PB.

Oleh itu, (m_AP)(m_PB) = –1.

(m_AP)(m_PB) = –1

(\frac{y - 2}{x - 0}) (\frac{y - 5}{x - 6}) = - 1

(y – 2)(y – 5) = – x(x – 6)

y² – 7y + 10 = –x² + 6x

y² + x² – 6x – 7y + 10 = 0

Persamaan lokus bagi titik P ialah,

y² + x² – 6x – 7y + 10 = 0

Soalan 8:

Cari persamaan pembahagi dua sama serenjang bagi garis lurus yang menyambungkan titik (–4, 3) dengan titik (2, 4).

Penyelesaian:

Kecerunan garis, m₁=

\frac{4 - 3}{2 - (- 4)} = \frac{1}{6}

Kecerunan garis serenjang, m₂ =

- \frac{1}{m_{1}} = - 6

\begin{array}{l} Titik tengah = (\frac{- 4 + 2}{2}, \frac{3 + 4}{2}) \\ = (- 1, \frac{7}{2}) \end{array}

Jadi, persamaan pembahagi dua sama serenjang ialah

\begin{array}{l} y - \frac{7}{2} = - 6 (x - (- 1)) \\ y - \frac{7}{2} = - 6 x - 6 \end{array}

2y – 7 = –12x – 12

12x + 2y + 5 = 0

Bab 15 Vektor

Posted on July 7, 2016 by user

4.7 Vektor, SPM Praktis (Kertas 2)

Soalan 3:

Dalam rajah di bawah, PQRS ialah satu segi empat. PTSdan TUR ialah garis lurus.

Diberi bahawa

\vec{P Q} = 20 \underset{˜}{x}, \vec{P T} = 8 \underset{˜}{y}, \vec{S R} = 25 \underset{˜}{x} - 24 \underset{˜}{y}, \vec{P T} = \frac{1}{4} \vec{P S} dan \vec{T U} = \frac{3}{5} \vec{T R}

(a) Ungkapakan dalam sebutan

\underset{˜}{x} dan/ atau \underset{˜}{y} :

(i)

\vec{Q S}

(ii)

\vec{T R}

(b) Tunjukkan titik Q, Udan S adalah segaris.

| \underset{˜}{x} | = 2 dan | \underset{˜}{y} | = 3, cari | \vec{Q S} |

Penyelesaian:

(a)

\begin{array}{l} \vec{Q S} = \vec{Q P} + \vec{P S} \\ \vec{Q S} = - 20 \underset{˜}{x} + 32 \underset{˜}{y} \leftarrow \begin{array}{l} Diberi \vec{P T} = \frac{1}{4} \vec{P S} \\ \vec{P S} = 4 \vec{P T} = 4 (8 \underset{˜}{y}) = 32 \underset{˜}{y} \end{array} \end{array}

(b)

\begin{array}{l} \vec{T R} = \vec{T S} + \vec{S R} \\ \vec{T R} = \frac{3}{4} \vec{P S} + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = \frac{3}{4} (32 \underset{˜}{y}) + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = 24 \underset{˜}{y} + 25 \underset{˜}{x} - 24 \underset{˜}{y} \\ \vec{T R} = 25 \underset{˜}{x} \end{array}

(c)

\begin{array}{l} \vec{Q U} = \vec{Q P} + \vec{P T} + \vec{T U} \\ \vec{Q U} = - 20 \underset{˜}{x} + 8 \underset{˜}{y} + \frac{3}{5} (25 \underset{˜}{x}) \leftarrow \begin{array}{l} Diberi \\ \vec{T U} = \frac{3}{5} \vec{T R} \end{array} \\ \vec{Q U} = - 20 \underset{˜}{x} + 8 \underset{˜}{y} + 15 \underset{˜}{x} \\ \vec{Q U} = - 5 \underset{˜}{x} + 8 \underset{˜}{y} \end{array}

\begin{array}{l} Dari (a)(i) \vec{Q S} = - 20 \underset{˜}{x} + 32 \underset{˜}{y} \\ \frac{\vec{Q S}}{\vec{Q U}} = \frac{- 20 \underset{˜}{x} + 32 \underset{˜}{y}}{- 5 \underset{˜}{x} + 8 \underset{˜}{y}} \\ \frac{\vec{Q S}}{\vec{Q U}} = \frac{4 (- 5 \underset{˜}{x} + 8 \underset{˜}{y})}{(- 5 \underset{˜}{x} + 8 \underset{˜}{y})} \\ \frac{\vec{Q S}}{\vec{Q U}} = 4 \\ \vec{Q S} = 4 \vec{Q U} \end{array}

Oleh itu, Q, U dan S adalah segaris.

(d)

\begin{array}{l} \vec{P S} = 32 \underset{˜}{y} \\ | \vec{P S} | = 32 | \underset{˜}{y} | \\ | \vec{P S} | = 32 \times 3 = 96 \\ \vec{P Q} = 20 \underset{˜}{x} \\ | \vec{P Q} | = 20 | \underset{˜}{x} | \\ | \vec{P Q} | = 20 \times 2 = 40 \\ Oleh itu | \vec{Q S} | = \sqrt{96^{2} + 40^{2}} \\ | \vec{Q S} | = 104 \end{array}

Bab 15 Vektor

Posted on July 6, 2016 by user

4.7 Vektor, SPM Praktis (Kertas 2)

Soalan 1:

Rajah di atas menunjukkan segi tiga OAB. Garis lurus AP bersilang dengan garis lurus OQpada titik R.

Diberi bahawa

O P = \frac{1}{4} O B, A Q = \frac{1}{4} A B, \vec{O P} = 4 \underset{˜}{b} dan \vec{O A} = 8 \underset{˜}{a} .

(a) Ungkapakan dalam sebutan

\underset{˜}{a} dan \underset{˜}{b} :

(i)

\vec{A P}

(ii)

\vec{O Q}

(b) (i) Diberi bahawa

\vec{A R} = h \vec{A P}, nyatakan \vec{A R} dalam sebutan h, \underset{˜}{a} dan \underset{˜}{b} .

(ii) Diberi bahawa

\vec{R Q} = k \vec{O Q}, nyatakan \vec{A R} dalam sebutan k, \underset{˜}{a} dan \underset{˜}{b} .

\vec{A Q} = \vec{A R} + \vec{R Q},

cari nilai bagi h dan k.

Penyelesaian:

(a)(i)

\begin{array}{l} \vec{A P} = \vec{A O} + \vec{O P} \\ \vec{A P} = - \vec{O A} + \vec{O P} \\ \vec{A P} = - 8 \underset{˜}{a} + 4 \underset{˜}{b} \end{array}

(a)(ii)

\begin{array}{l} \vec{O Q} = \vec{O A} + \vec{A Q} \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} \vec{A B} \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (\vec{A O} + \vec{O B}) \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (- 8 \underset{˜}{a} + 4 \vec{O P}) \\ \vec{O Q} = 8 \underset{˜}{a} + \frac{1}{4} (- 8 \underset{˜}{a} + 4 (4 \underset{˜}{b})) \\ \vec{O Q} = 8 \underset{˜}{a} - 2 \underset{˜}{a} + 4 \underset{˜}{b} \\ \vec{O Q} = 6 \underset{˜}{a} + 4 \underset{˜}{b} \end{array}

(b)(i)

\begin{array}{l} \vec{A R} = h \vec{A P} \\ \vec{A R} = h (- 8 \underset{˜}{a} + 4 \underset{˜}{b}) \\ \vec{A R} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} \end{array}

(b)(ii)

\begin{array}{l} \vec{R Q} = k \vec{O Q} \\ \vec{R Q} = k (6 \underset{˜}{a} + 4 \underset{˜}{b}) \\ \vec{R Q} = 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \end{array}

(c)

\begin{array}{l} \vec{A Q} = \vec{A R} + \vec{R Q} \\ \vec{A Q} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + (6 k \underset{˜}{a} + 4 k \underset{˜}{b}) \\ \vec{A O} + \vec{O Q} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \\ - 8 \underset{˜}{a} + 6 \underset{˜}{a} + 4 \underset{˜}{b} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \\ - 2 \underset{˜}{a} + 4 \underset{˜}{b} = - 8 h \underset{˜}{a} + 4 h \underset{˜}{b} + 6 k \underset{˜}{a} + 4 k \underset{˜}{b} \end{array}

–2 = –8h + 6k

–1 = –4h + 3k → (1)

4 = 4h + 4k

1 = h + k

k= 1 – h → (2)

Gantikan (2) ke dalam (1),

–1 = –4h + 3 (1 – h)

–1 = –4h + 3 – 3h

–4 = –7h

\begin{array}{l} h = \frac{4}{7} \\ Daripada (2), \\ k = 1 - \frac{4}{7} = \frac{3}{7} \end{array}

Bab 5 Indeks dan Logaritma

Posted on July 6, 2016 by user

5.3 Persamaan yang Melibatkan Indeks (Contoh Soalan)

Contoh 5 [Asas tidak sama – tukar kepada bentuk lagaritma biasa (log₁₀) bagi kedua-dua belah]:

Selesaikan setiap persamaan yang berikut.

(a) 3^x ⁺ ¹ = 7
(b) 2 (3^x ) = 5
(c) 2^x .3^x = 9^x ⁻ ⁴
(d) 5^x ⁻ ¹.3^x ⁺ ² = 10

Penyelesaian:

Bab 5 Indeks dan Logaritma

Posted on July 6, 2016 by user

5.2 Logaritma

N = a^x ↔ log_aN = x

log_a N = x ialah bentuk logaritma manakala N = a^x ialah bentuk index.

Takrif Logaritma:

1. Jika aialah nombor positif, maka a^xjuga nombor positif. Logaritma bagi nombor negatif adalah tidak tertakrif.

2. Logaritma yang asasnya 10 dikenali sebagai logaritma biasa. Simbolnya ialah log₁₀, singkatannya lg.

3. Nilai logaritma biasa dapat dicari dengan menggunakan kalkulator saintifik.

4. Bagi asas logaritma bukan 10, asanya perlu dinyatakan, misalnya log₃81.

5. Logaritma boleh berasas sebarang nombor positif, kecuali 1,

(a) log_a1 = 0

(b) log_aa= 1

Contoh 1:

Cari persamaan-persamaan berikut:

(a) log₂ 64

(b) log₃ 1

(d) log_½ 4

(e) log₈ 0.25

Penyelesaian:

Contoh 2:

Cari persamaan-persamaan berikut:

(a) log₃ 5x = 2

(b) log_x_{+ 1} 81 = 2

Penyelesaian: