4.2 Pengkuantiti ‘Semua’ dan ‘Sebilangan’ (Contoh Soalan)
Soalan 1:
Dengan menggunakan pengkuantiti ‘semua’ atau ‘sebilangan’, lengkapkan setiap yang berikut supaya membentuk satu pernyataan benar.
(a)
_____ segi empat tepat adalah segi empat sama.
(b)
_____ nombor perdana adalah nombor ganjil.
(c)
_____ Segi tiga mempunyai sisi sama.
(d)
_____ nombor genap boleh dibahagi tepat dengan 2.
Penyelesaian:
(a)
Sebilangansegi empat tepat adalah segi empat sama.
(b)
Sebilangannombor perdana adalah nombor ganjil.
(c)
SebilanganSegi tiga mempunyai sisi sama.
(d)
Senuanombor genap boleh dibahagi tepat dengan 2.
Soalan 2:
Bina satu pernyataan benar dengan menggunakan pengkuantiti ‘semua’ atau ‘sebilangan’ berdasarkan objek dan ciri yang diberi.
(a)
Objek: nombor gandaan bagi 4
Ciri: boleh dibahagi tepat dengan 5
(b)
Objek: heksagon sekata.
Ciri: 6 sisi sama.
(c)
Objek: sudut tirus
Ciri: kurang daripada 90o
Penyelesaian:
(a)
Sebilangan nombor gandaan bagi 4 boleh dibahagi tepat dengan 5.
(b)
Semua heksagon sekata mempunyai 6 sisi sama.
(c)
Semua sudut tirus adalah kurang daripada 90o.
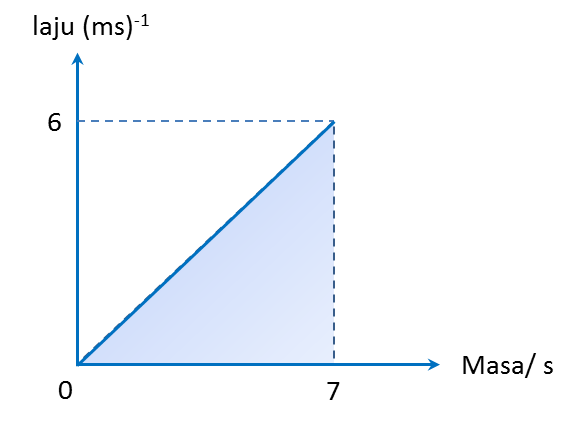
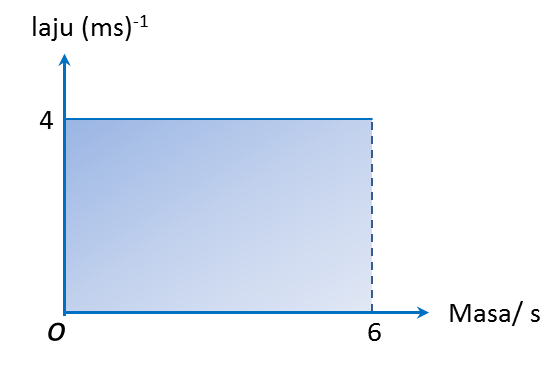
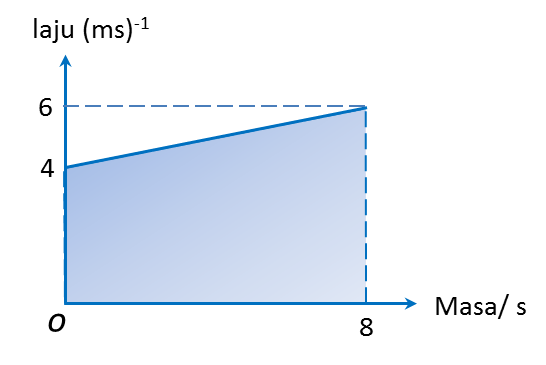
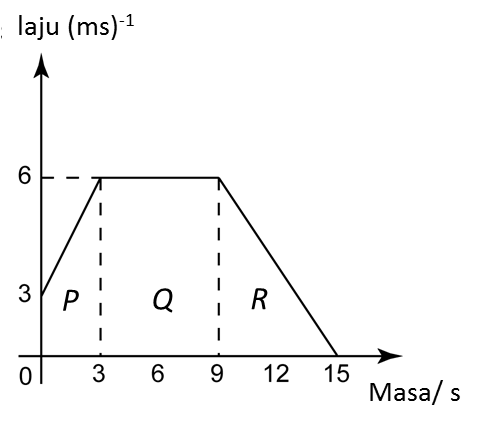
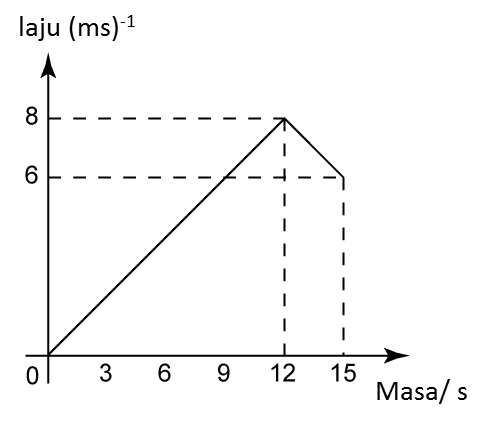
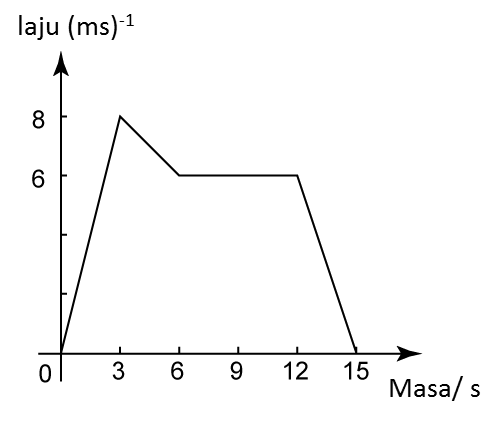


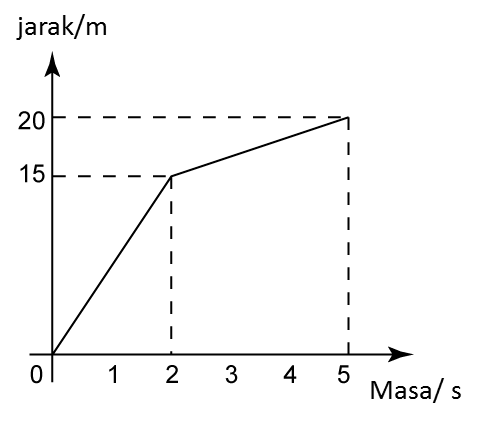
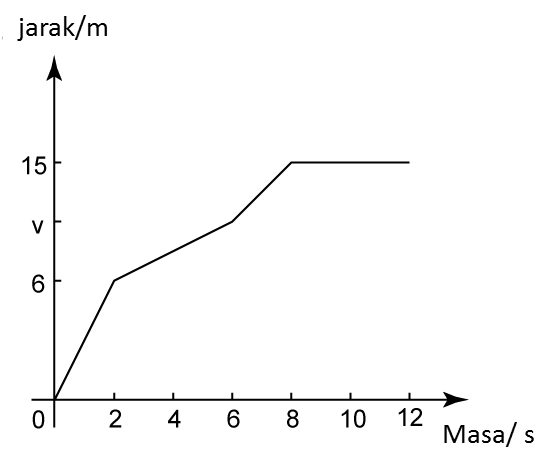
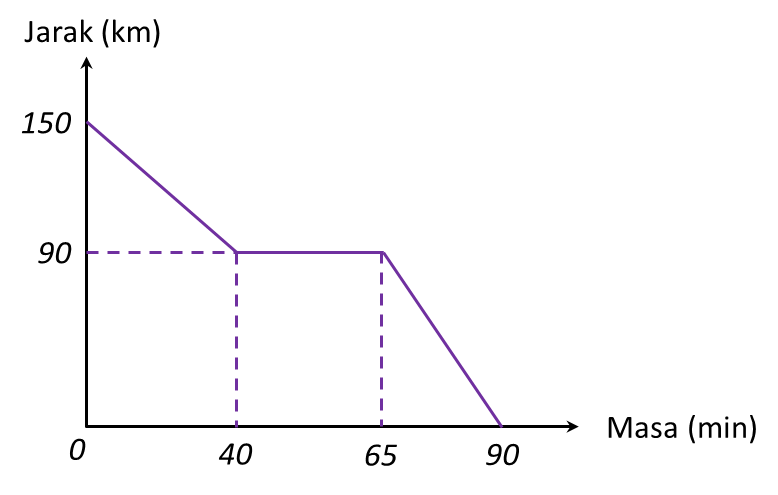
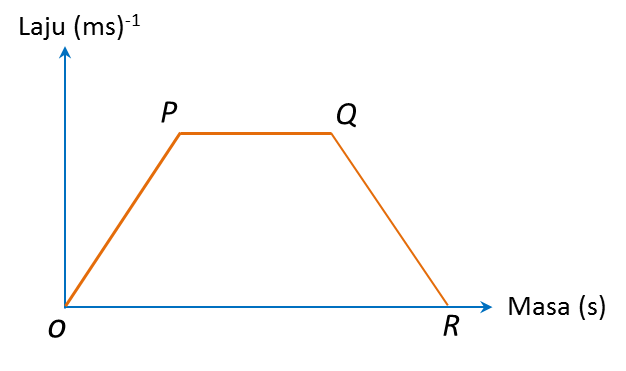
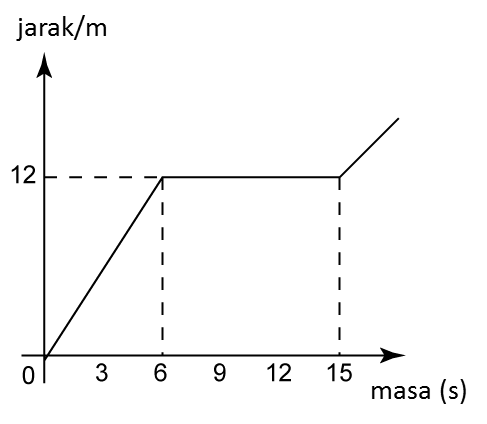
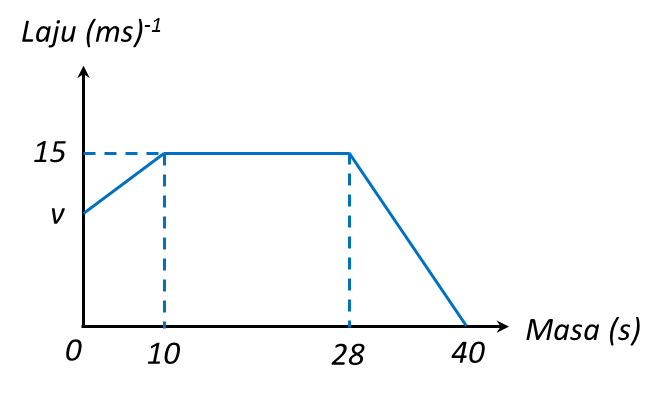 (a) Nyatakan tempoh masa, dalam s, objek itu bergerak dengan laju seragam.
(a) Nyatakan tempoh masa, dalam s, objek itu bergerak dengan laju seragam.