Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

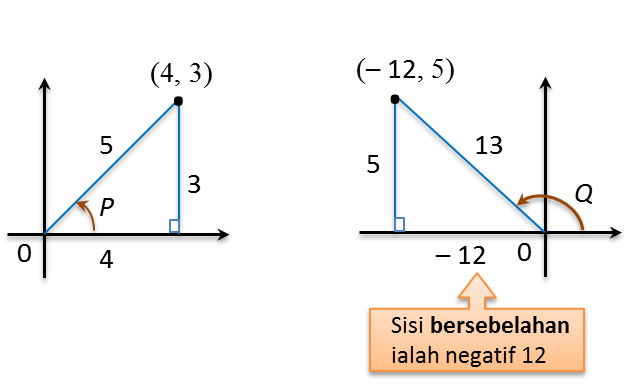
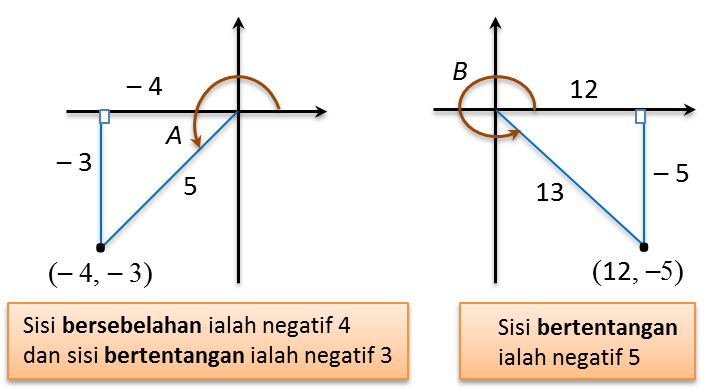
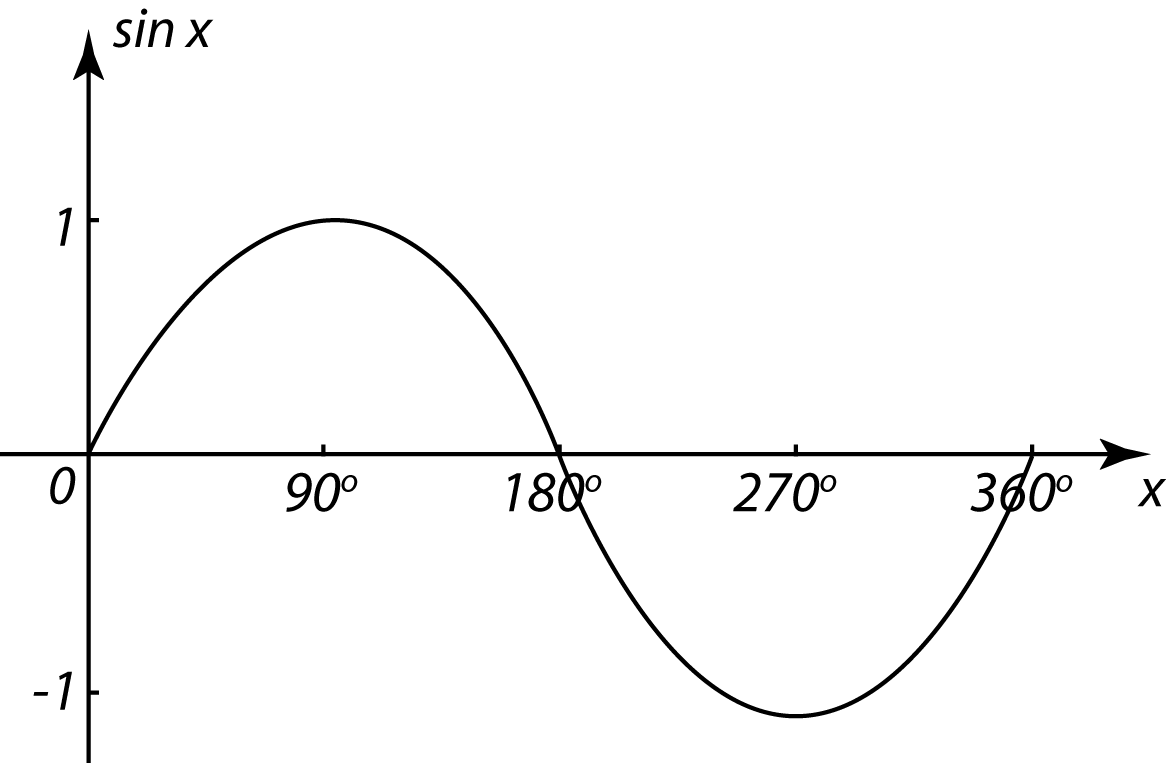
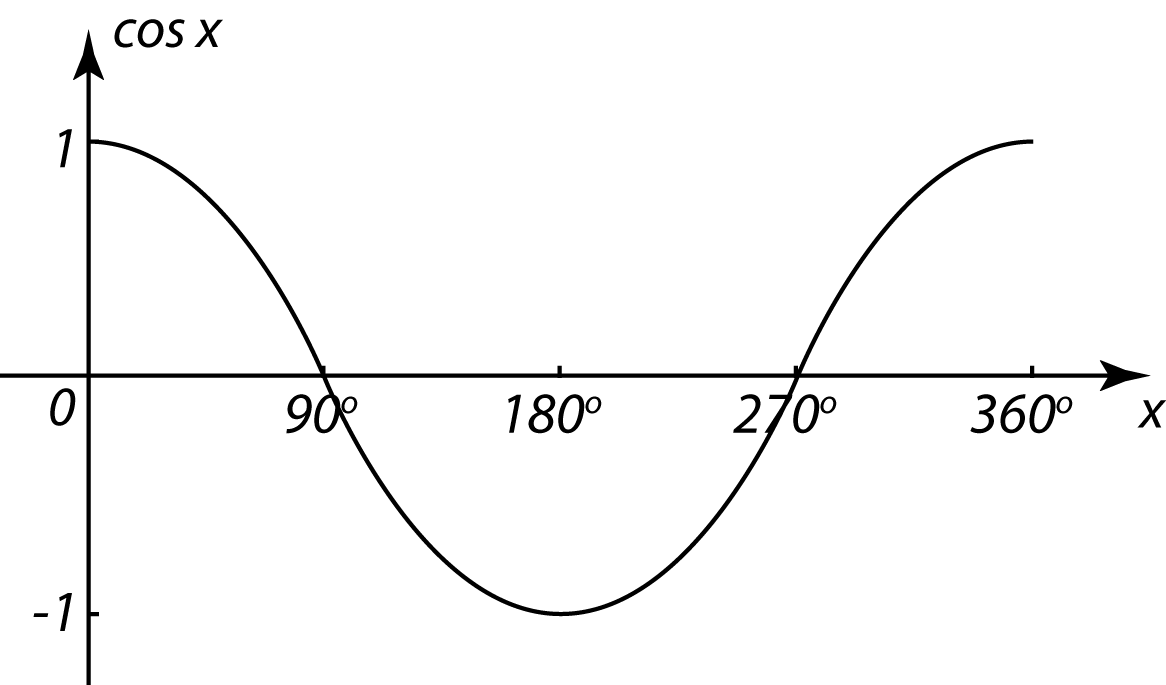
5.6.3 Bentuk Persamaan Kuadratik dalam sin x/ kos x/ tan x/ kosek x/ sek x/ kot x

Contoh:

Cari semua sudut di antara 0° dan 360° yang boleh menyelesaikan persamaan yang berikut.

(a) 3 sin² x – 2 sin x – 1 = 0

(b) 2 sin x = kosek x + 1

(d) 2 sek x = 1 + kos x

(e) 2 kot² x + 8 = 7 kosek x

Penyelesaian:

(a)

3 sin² x – 2 sin x – 1 = 0

(3 sin x + 1)(sin x – 1) = 0

sin x = –⅓ , sin x = 1

sin x = –⅓

sudut asas x = 19.47^o

x= 180^o + 19.47^o, 360^o – 19.47^o

x = 199.47^o, 340.53^o

sin x = 1, x = 90^o

Oleh itu x = 90^o, 199.47^o, 340.53^o

(b)

2 sin x = kosek x + 1

$2 \sin x = \frac{1}{\sin x} + 1$

2 sin² x = 1 + sin x

2 sin² x – sin x – 1 = 0

(2 sin x + 1)(sin x – 1) = 0

sin x = –½ , sin x = 1

sin x = –½

sudut asas x = 30^o

x= 180^o + 30^o, 360^o – 30^o

x = 210^o, 330^o

sin x = 1, x = 90^o

Oleh itu x = 90^o, 210^o, 330^o

(c)

5 sin²x= 2(1 + kos x)

5 (1 – kos² x) = 2 + 2 kos x

5 – 5 kos² x – 2 – 2 kos x = 0

–5 kos² x – 2 kos x + 3 = 0

5 kos² x + 2 kos x – 3 = 0

(5 kos x – 3)(kos x + 1) = 0

$\begin{array}{l} k o s x = \frac{3}{5}, k o s x = - 1 \\ k o s x = \frac{3}{5} \end{array}$

sudut asas x = 53.13^o

x= 53.13^o, 360^o – 53.13^o

cos x = – 1

x= 180^o

Oleh itu x = 53.13^o, 180^o, 306.87^o

(d)

2 sek x = 1 + kos x

$\frac{2}{k o s x} = 1 + k o s x$

2 = kos x + kos² x

kos² x+ kos x – 2 = 0

(kos x – 1)(kos x + 2) = 0

kos x = 1

x= 0^o, 360^o

kos x = –2 (tidak diterima)

Oleh itu x = 0^o, 360^o

(e)

2 kot² x + 8 = 7 kosek x

2 (kosek²x – 1) + 8 = 7 kosek x

2 kosek²x – 2 – 7 kosek x + 8 = 0

2 kosek²x – 7 kosek x + 6 = 0

(2 kosek x – 3)(kosek x – 2) = 0

$\begin{array}{l} k o s e k x = \frac{3}{2}, k o s e k x = 2 \\ \sin x = \frac{2}{3}, \sin x = \frac{1}{2} \\ \sin x = \frac{2}{3} \end{array}$

sudut asas x = 41.81^o

x= 41.81^o, 180^o – 41.81^o

sin x = ½

sudut asas x = 30^o

x= 30^o, 180^o– 30^o

Oleh itu x = 30^o, 41.81^o, 138.19^o, 150^o

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.6.2 Menyelesaikan Persamaan Trigonometri (Pemfaktoran)

Contoh:

Cari semua sudut untuk 0° ≤ x ≤ 360° yang boleh selesaikan setiap persamaan trigonometri yang berikut.

(a) kot x = –2 kos x

(b) 3 sek x = 4 kos x

Penyelesaian:

(a)

kot x = –2 kos x

$\frac{\cos x}{\sin x} = - 2 \cos x$

kos x = –2 kos x sin x

kos x + 2 sin x kos x = 0

kos x (1 + 2 sin x ) = 0

kos x = 0

x= 90^o, 270^o

1 + 2 sin x= 0

sin x = –½

∠asas x = 30^o

x = (180^o + 30^o), (360^o – 30^o)

x= 210^o, 330^o

Oleh itu, x= 90^o, 210^o, 270^o, 330^o

(b)

$\begin{array}{l} 3 sek x = 4 k o s x \\ \frac{3}{k o s x} = 4 k o s x \\ 3 = 4 k o s^{2} x \\ k o s^{2} x = \frac{3}{4} \\ k o s x = \pm \frac{\sqrt{3}}{2} \\ ∠ asas = 30^{\circ} \\ x = 30^{\circ}, (180^{\circ} - 30^{\circ}), (180^{\circ} + 30^{\circ}), (360^{\circ} - 30^{\circ}) \\ x = 30^{\circ}, 150^{\circ}, 210^{\circ}, 330^{\circ} \end{array}$

(c)

$\begin{array}{l} 16 \tan x = k o t x \\ 16 \tan x = \frac{1}{\tan x} \\ \tan^{2} x = \frac{1}{16} \\ \tan x = \pm \frac{1}{4} \\ ∠ asas = {14.04}^{\circ} \\ x = {14.04}^{\circ}, (180^{\circ} - {14.04}^{\circ}), \\ (180^{\circ} + {14.04}^{\circ}), (360^{\circ} - {14.04}^{\circ}) \\ x = {14.04}^{\circ}, {165.96}^{\circ}, {194.04}^{\circ}, {345.96}^{\circ} \end{array}$

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.6 Menyelesaikan Persamaan Trigonometri

5.6.1 Persamaan asas dalam sin x/ kos x/ tan x/ kosek x/ sek x/ kot x

Langkah-langkah untuk menyelesaikan persamaan trigonometri:

(1) Tentukan julat bagi nilai-nilai sudut yang berkenaan.

(2) Cari sudut asas dengan menggunakan kalkulator.

(3) Tentukan kedudukan sukuan bagi sudut-sudut.

(4) Tentukan nilai bagi sudut yang berada dalam sukuan itu.

Contoh:

Cari nilai-nilai quntuk 0° < q < 360° yang memuaskan setiap persamaan trigonometri yang berikut.

(a) sin θ = 0.6137

(b) cos q = 0.2377

(d) sin q = –0.8537

(e) sin 2q = 0.5293

Penyelesaian:

(a)

sin q= 0.6137

∠asas= sin^-10.6137 = 37.86^o

q = 37.86° 180°-37.86°

q = 37.86°, 142.14°

(b)

kos q = 0.2377

∠asas = cos^-10.2377 = 76.25°

q = 76.25°, 360° – 76.25°

q = 76.25°, 283.75°

(c)

tan q = 2.7825

∠asas = tan^-12.7825 = 70.23°

q = 70.23°, 180° + 70.23°

q = 70.23°, 250.23°

(d)

sin q = –0.8537

∠asas = sin^-10.8537 = 58.62°

q = 180° + 58.62°, 360° – 58.62°

q = 238.62°, 301.38°

(e)

sin 2q = 0.5293

∠ asas = 31.96°

0° < q < 360°

0° < 2q < 720°

2q = 31.96°, 180° – 31.96°, 360° + 31.96°, 360° + 180° – 31.96°

2q = 31.96°, 148.04°, 360° + 391.96°, 508.04°

q = 15.98°, 74.02°, 195.98°, 254.02°

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.5.1 Rumus bagi sin (A ± B), kos (A ± B), tan (A ± B), sin 2A, kos 2A, tan 2A
(Contoh Soalan)

Contoh 2:

Buktikan setiap identity trigonometri yang berikut.

$\begin{array}{l} (a) \frac{1 + k o s 2 x}{\sin 2 x} = k o t x \\ (b) k o t A sek 2 A = k o t A + \tan 2 A \\ (c) \frac{s i n x}{1 - k o s x} = k o t \frac{x}{2} \end{array}$

Penyelesaian:

(a)

$\begin{array}{l} S e b e l a h k i r i \\ = \frac{1 + k o s 2 x}{\sin 2 x} \\ = \frac{1 + (2 k o s^{2} x - 1)}{2 \sin x k o s x} \\ = \frac{2 k o s^{2} x}{2 \sin x k o s x} \\ = \frac{k o s x}{\sin x} \\ = k o t x = S e b e l a h k a n a n \end{array}$

(b)

$\begin{array}{l} S e b e l a h k a n a n \\ = k o t A + \tan 2 A \\ = \frac{k o s A}{\sin A} + \frac{\sin 2 A}{k o s 2 A} \\ = \frac{k o s A k o s 2 A + \sin A \sin 2 A}{\sin A k o s 2 A} \\ = \frac{k o s A (k o s^{2} A - \sin^{2} A) + \sin A (2 \sin A k o s A)}{\sin A k o s 2 A} \end{array}$

$\begin{array}{l} = \frac{k o s^{3} A - k o s A \sin^{2} A + 2 \sin^{2} A k o s A}{\sin A k o s 2 A} \\ = \frac{k o s^{3} A + k o s A \sin^{2} A}{\sin A k o s 2 A} \\ = \frac{k o s A (k o s^{2} A + \sin^{2} A)}{\sin A k o s 2 A} \\ = \frac{k o s A}{\sin A k o s 2 A} \leftarrow \sin^{2} A + k o s^{2} A = 1 \\ = (\frac{k o s A}{\sin A}) (\frac{1}{k o s 2 A}) \\ = k o t A sek 2 A \\ = S e b e l a h k i r i \end{array}$

(c)

$\begin{array}{l} S e b e l a h k i r i \\ = \frac{s i n x}{1 - k o s x} \\ = \frac{2 s i n \frac{x}{2} k o s \frac{x}{2}}{1 - (1 - 2 s i n^{2} \frac{x}{2})} \leftarrow \begin{array}{l} \sin x = 2 s i n \frac{x}{2} k o s \frac{x}{2}, \\ k o s x = 1 - 2 \sin^{2} \frac{x}{2} \end{array} \\ = \frac{2 s i n \frac{x}{2} k o s \frac{x}{2}}{2 s i n^{2} \frac{x}{2}} = \frac{k o s \frac{x}{2}}{s i n \frac{x}{2}} \\ = k o t \frac{x}{2} = S e b e l a h k a n a n \end{array}$

Contoh 3:

(a) Diberi bahawa

$\sin P = \frac{3}{5} dan \sin Q = \frac{5}{13},$ dengan keadaan P ialah satu sudut tirus dan Q ialah satu sudut cakah, tanpa menggunakan sifir atau kalkulator, cari nilai kos (P + Q).

(b) Diberi bahawa

$\sin A = - \frac{3}{5} dan \sin B = \frac{12}{13},$ dengan keadaan A dan B adalah sudut-sudut dalam sukuan III dan sukuan IV masing-masing, tanpa menggunakan sifir atau kalkulator, cari nilai sin (A – B).

Penyelesaian:

(a)

$\begin{array}{l} \sin P = \frac{3}{5}, k o s P = \frac{4}{5} \\ \sin Q = \frac{5}{13}, k o s Q = - \frac{12}{13} \\ k o s (P + Q) \\ = k o s A k o s B - \sin A \sin B \\ = (\frac{4}{5}) (- \frac{12}{13}) - (\frac{3}{5}) (\frac{5}{13}) \\ = - \frac{48}{65} - \frac{15}{65} \\ = - \frac{63}{65} \end{array}$

(b)

$\begin{array}{l} \sin A = - \frac{3}{5}, k o s A = - \frac{4}{5} \\ \sin B = - \frac{5}{13}, k o s B = \frac{12}{13} \\ s i n (A - B) \\ = s i n A k o s B - k o s A \sin B \\ = (- \frac{3}{5}) (\frac{12}{13}) - (- \frac{4}{5}) (- \frac{5}{13}) \\ = - \frac{36}{65} - \frac{20}{65} \\ = - \frac{56}{65} \end{array}$

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.5 Rumus bagi sin (A ± B), kos (A ± B), tan (A ± B), sin 2A, kos 2A, tan 2A

Rumus penambahan

$\begin{array}{l} • \sin A = 2 \sin \frac{A}{2} k o s \frac{A}{2} \\ • k o s A = \sin^{2} \frac{A}{2} - k o s^{2} \frac{A}{2} \\ k o s A = 2 k o s^{2} \frac{A}{2} - 1 \\ k o s A = 1 - 2 k o s^{2} \frac{A}{2} \\ • \tan A = \frac{2 \tan \frac{A}{2}}{1 - \tan^{2} \frac{A}{2}} \end{array}$

5.5.1 Pembuktian Identiti Trigonometri yang Melibatkan Sudut Majmuk dan Sudut Berganda

Contoh 1:

Buktikan setiap identity trigonometri yang berikut.

$\begin{array}{l} (a) \frac{s i n (A + B) - s i n (A - B)}{k o s A k o s B} = 2 \tan B \\ (b) \frac{k o s (A + B)}{\sin A k o s B} = k o t A - \tan B \\ (c) \tan (A + 45^{o}) = \frac{\sin A + k o s A}{k o s A - \sin A} \end{array}$

penyelesaian:

(a)

$\begin{array}{l} (S e b e l a h K i r i) \\ = \frac{s i n (A + B) - s i n (A - B)}{k o s A k o s B} \\ = \frac{(\sin A k o s B + k o s A \sin B) - (\sin A k o s B - k o s A \sin B)}{k o s A k o s B} \\ = \frac{2 k o s A \sin B}{k o s A k o s B} \\ = \frac{2 \sin B}{k o s B} \\ = 2 \tan B = (S e b e l a h K a n a n) \end{array}$

(b)

$\begin{array}{l} (S e b e l a h K i r i) \\ = \frac{k o s (A + B)}{\sin A k o s B} \\ = \frac{k o s A k o s B - \sin A \sin B}{\sin A k o s B} \\ = \frac{k o s A k o s B}{\sin A k o s B} - \frac{\sin A \sin B}{\sin A k o s B} \\ = \frac{k o s A}{\sin A} - \frac{\sin B}{k o s B} \\ = k o t A - \tan B \\ = (S e b e l a h K a n a n) \end{array}$

(c)

$\begin{array}{l} (S e b e l a h K i r i) \\ = \tan (A + 45^{o}) \\ = \frac{t a n A + \tan 45^{o}}{1 - t a n A \tan 45^{o}} \\ = \frac{t a n A + 1}{1 - t a n A} \leftarrow \tan 45^{o} = 1 \\ = \frac{\frac{\sin A}{k o s A} + 1}{1 - \frac{\sin A}{k o s A}} \\ = \frac{\sin A + k o s A}{k o s A} \times \frac{k o s A}{k o s A - \sin A} \\ = \frac{\sin A + k o s A}{k o s A - \sin A} \\ = (S e b e l a h K a n a n) \end{array}$

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.4 Identiti Asas

sin² x + kos² x = 1

sek² x = 1 + tan² x

kosek² x = 1 + kot² x

Contoh 1 (Pembuktian Identiti Trigonometri dengan Menggunakan Identiti Asas)

Buktikan setiap identity trigonometri yang berikut.

(a) sin²x – kos² x = 1 – 2 kos² x

(b) (1 – kosek²x) (1– sek² x) = 1

Penyelesaian:

(a)

sin²x– kos² x = 1 – 2 kos²x

Sebelah kiri: sin²x– kos² x

= 1 – kos² x – kos² x

= 1 – 2 kos² x (Sebelah kanan)

(b)

(1 – kosek²x) (1– sek² x) = 1

Sebelah kiri: (1 – kosek²x) (1– sek² x)

= (–kot²x) (–tan² x)

= (kot²x) (tan² x)

$\begin{array}{l} = (\frac{1}{\tan^{2} x}) \tan^{2} x \\ = 1 (Sebelah kanan) \end{array}$

(c)

kot²x – kot² x kos² x = kos² x

Sebelah kiri: kot²x– kot² x kos² x

= kot²x (1 – kos²x)

= kot²x (sin²x)

$\begin{array}{l} = \frac{k o s^{2} x}{s i n^{2} x} (s i n^{2} x) \\ = k o s^{2} x (Sebelah kanan) \end{array}$

Contoh 2 (Menyelesaikan Persamaan Trigonometri dengan Identiti Asas)

Selesaikan setiap persamaan trigonometri yang berikut untuk 0^o ≤ x ≤ 360^o.

(a) sin²x kos x + 1 = kos x

(b) 2 kosek²x – 5 kot x = 0

Penyelesaian:

(a)

sin²x kos x + 1 = kos x

(1 – kos²x) kos x + 1 = kos x

kos x – kos³x + 1 = kos x

kos³x = 1

kos x = 1

x = 0^o, 360^o

(b)

2 kosek²x – 5 kot x = 0

2 (1 + kot²x) – 5 kot x = 0

2 + 2 kot²x – 5 kot x = 0

2 kot²x – 5 kot x + 2 = 0

(2 kotx – 1) (kot x – 2) = 0

kotx = ½ atau kot x = 2

kotx = ½ atau kotx = 2

tan x = 2, tan x = ½

x =63.43^o, 243.43^o , x = 26.57^o, 206.57^o

(Perhatian: tangen adalah positif dalam sukuan I dan III)

Oleh itu, x = 26.57^o, 63.43^o, 206.57^o, 243.43^o

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.3.2c Melakar Graf Fungsi Trigonometri (Bahagian 3)

Contoh 2:

(a) Lakar graf bagi y = –½ kos x untuk 0 ≤ x ≤ 2π.

(b) Seterusnya, dengan menggunakan paksi yang sama, lakar satu graf yang sesuai untuk mencari bilangan penyelesaian bagi persamaan

$\frac{π}{2 x} + k o s x = 0$ untuk 0 ≤ x ≤ 2π.

Nyatakan bilangan penyelesaian itu.

Penyelesaian:

(a)

(b)

$\begin{array}{l} \frac{π}{2 x} + k o s x = 0 \\ \frac{π}{2 x} = - k o s x \\ \frac{π}{4 x} = - \frac{1}{2} k o s x \leftarrow \begin{array}{l} darab kedua-dua \\ belah dengan \frac{1}{2} \end{array} \\ y = \frac{π}{4 x} \leftarrow y = - \frac{1}{2} k o s x \end{array}$

Graf yang sesuai ialah

$y = \frac{π}{4 x} .$