Question 6:
Puan Rafidah wants to prepare a right circular cone shaped container in order to fill it with candies for her family Hari Raya Celebration. Diagram below shows the net of a right circular cone.

The circumference of the lid is 44 cm and its height is 24 cm.
Calculate the volume, in cm3 , of the container.
[π=227]
Solution:
2πr=442×227×r=44 r=442×722 r=7 cmVolume of cone=13πr2h =13×227×72×24 =1232 cm3
Puan Rafidah wants to prepare a right circular cone shaped container in order to fill it with candies for her family Hari Raya Celebration. Diagram below shows the net of a right circular cone.

The circumference of the lid is 44 cm and its height is 24 cm.
Calculate the volume, in cm3 , of the container.
[π=227]
Solution:
2πr=442×227×r=44 r=442×722 r=7 cmVolume of cone=13πr2h =13×227×72×24 =1232 cm3
Question 7:
A barrel contains 36 l of mineral water. ⅔ of the mineral water is mixed with 6 bottles of syrup, with a volume of 1.5 l each. The drink will be poured into a number of bottles with the same volume of 300 ml.
How many number of bottles needed?
Solution:
Volume of mineral water=23×36 l=24 lVolume of syrup=6×1.5 l=9 lTotal volume=24+9=33 l=33000 mlNumber of bottles needed=33000300=110
A barrel contains 36 l of mineral water. ⅔ of the mineral water is mixed with 6 bottles of syrup, with a volume of 1.5 l each. The drink will be poured into a number of bottles with the same volume of 300 ml.
How many number of bottles needed?
Solution:
Volume of mineral water=23×36 l=24 lVolume of syrup=6×1.5 l=9 lTotal volume=24+9=33 l=33000 mlNumber of bottles needed=33000300=110
Question 8:
A spherical balloon expands such that its volume increases from 36π cm3 to 288π cm3 .
Find the increment of the radius, in cm, of the balloon.
Solution:
V1=43πr1343πr13=36πr13=36π×34πr13=27r1=3 cmV2=43πr2343πr23=288πr23=288π×34πr23=216r2=6 cmIncrement=r2−r1=6−3=3 cm
A spherical balloon expands such that its volume increases from 36π cm3 to 288π cm3 .
Find the increment of the radius, in cm, of the balloon.
Solution:
V1=43πr1343πr13=36πr13=36π×34πr13=27r1=3 cmV2=43πr2343πr23=288πr23=288π×34πr23=216r2=6 cmIncrement=r2−r1=6−3=3 cm
Question 9:
A boy is given three pieces of cards by his teacher. The cards consist of one rectangle card and two circle cards of the same size as shown in the diagram below. The circumference of each circle is 66 cm.
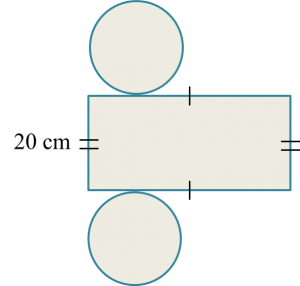
He is required to combine the cards to form a right circular cylinder.
Calculate the volume, in cm3, of the right circular cylinder.
Solution:
2πr=662×227×r=66 r=66×72×22 =10.5 cmVolume=πr2h =227×10.52×20 =6930 cm3
A boy is given three pieces of cards by his teacher. The cards consist of one rectangle card and two circle cards of the same size as shown in the diagram below. The circumference of each circle is 66 cm.

He is required to combine the cards to form a right circular cylinder.
Calculate the volume, in cm3, of the right circular cylinder.
Solution:
2πr=662×227×r=66 r=66×72×22 =10.5 cmVolume=πr2h =227×10.52×20 =6930 cm3
Question 10:
Diagram below shows cube P and cube Q with the total surface area of 726 cm2 and 1014 cm2 respectively.
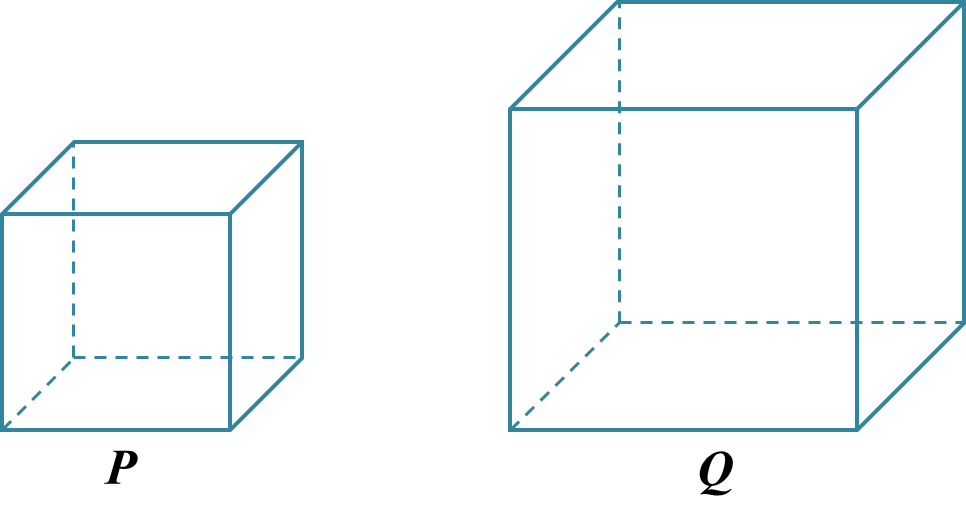 Find the difference in volume between cube P and cube Q.
Find the difference in volume between cube P and cube Q.
Solution:
Area of one surface area of cube P=7266=121 cm2x(Length)×x(Width)=121 x2=121 x=11Area of one surface area of cube Q=10146=169 cm2y(Length)×y(Width)=169 y2=169 y=13Difference in volume=133−113=2197−1331=866 cm3
Diagram below shows cube P and cube Q with the total surface area of 726 cm2 and 1014 cm2 respectively.
 Find the difference in volume between cube P and cube Q.
Find the difference in volume between cube P and cube Q.Solution:
Area of one surface area of cube P=7266=121 cm2x(Length)×x(Width)=121 x2=121 x=11Area of one surface area of cube Q=10146=169 cm2y(Length)×y(Width)=169 y2=169 y=13Difference in volume=133−113=2197−1331=866 cm3